W pobliżu północnego bieguna nieba, pomiędzy gwiazdozbiorami Małej Niedźwiedzicy, Kasjopei oraz Łabędzia znajduje się Cefeusz (łac. Cepheus)...

Zgodnie z powszechnie akceptowaną teorią Wielkiego Wybuchu dawno temu Wszechświat był bardzo gęsty i gorący, a w wyniku rozszerzania się stał się duży i chłodny, czyli taki jak obecnie. Hipotezę Wielkiego Wybuchu potwierdzają obserwacje „uciekających” we wszystkie strony galaktyk oraz poczerwienienia ich światła. Za Wielkim Wybuchem przemawia także obserwacja mikrofalowego promieniowania tła, wypełniającego w miarę równomiernie przestrzeń kosmiczną.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Czwartego lipca 2012 roku zespoły badawcze ATLAS i CMS wspólnie ogłosiły odkrycie nowej cząstki, znalezionej w trakcie poszukiwania bozonu Higgsa, ostatniego nieodkrytego obiektu przewidywanego przez Model Standardowy oddziaływań elementarnych (MS).

W termodynamice charakteryzujemy równowagowy układ za pomocą pewnego zbioru parametrów (np. ciśnienia, objętości i temperatury) i związków pomiędzy nimi (np. równania stanu gazu). Wielkości te są funkcjami stanu, a więc są jednoznacznie przyporządkowane danemu stanowi układu i nie zmieniają się w czasie. Jeśli jednak spojrzymy na układ z punktu widzenia jego struktury mikroskopowej, na cząsteczki gazu w ciągłym ruchu, powstaje pytanie: jak powiązać charakterystyki termodynamiczne układu z jego mikroskopową dynamiką?

„Tato, jak policzyć do nieskończoności?” – takie pytanie zadał mi niedawno mój czteroletni syn. Odpowiedziałem coś w stylu „nigdy nie skończysz”. W każdym razie liczenie do nieskończoności może się relatywnie szybko znudzić, może więc to zadanie, jak wiele innych monotonnych zadań, powierzyć komputerowi? A czy komputer potrafi policzyć do nieskończoności?

Dla mnie odpowiedź nie jest oczywista. W pierwszej chwili pomyślałem, że nie jest potrzebna, ale to było sprowokowane samym pytaniem.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Na nieskończoności opierają się konstrukcje większości obiektów analizy matematycznej, choć często w niejawny sposób. Przyjrzyjmy się choćby ciągłości – pojęciu na pierwszy rzut oka z nieskończonością niezwiązanemu. Można powiedzieć, że funkcja jest ciągła, jeśli „nie rozrywa” dziedziny...

Kombinatoryka zajmuje się własnościami zbiorów skończonych, w szczególności zagadnieniem zliczania elementów takich zbiorów. Czy może zatem w kombinatoryce znaleźć się miejsce dla nieskończoności? Okazuje się, że tak – pokażę jedno z takich zastosowań nieskończoności: funkcje tworzące...

Po to, żeby twierdzenie o pełności zachodziło.

A w ósmy dzień Bóg stworzył liczby pierwsze. I stworzył ich nieskończenie wiele. I widział, że to było dobre. (apokryf z XXI wieku)

Często pojawiające się w matematyce zadanie polega na skonstruowaniu funkcji 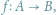 spełniającej pewne warunki. Między innymi możemy chcieć, aby funkcja ta była różnowartościowa i „na”, co gdyby miało miejsce, oznaczałoby równoliczność zbiorów 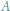i 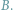 Punktem wyjścia bywa inna funkcja 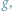 która potrzebnych warunków nie spełnia, ale wystarczy ją tylko trochę zmienić.

Czy nieskończoność jest tylko jedna? Nie, istnieją różne, większe i mniejsze!

Pojęcie nieskończoności można rozpatrywać z rozmaitych perspektyw. Poniżej spojrzymy na nie przez pryzmat równania Naviera–Stokesa, które opisuje przepływ nieściśliwych płynów.

Czy nieskończoność jest potrzebna matematykowi stosowanemu, tzn. takiemu, który chce, by jego struktury matematyczne opisywały świat? Matematyka stosowana to budowanie (tworzenie) i analizowanie modeli matematycznych, czyli takich struktur (najczęściej równań), które ujmują pewne aspekty opisywanej rzeczywistości.

Nawet w bardzo „młodych” gałęziach nauki zaczynają gromadzić się długoletnie rocznice, których nie wolno przegapić. Niepostrzeżenie, na przykład, okazuje się, że to już 60 lat minęło od ogłoszenia (wówczas) hipotezy o strukturze DNA. W samym odkryciu, oprócz tego, że okazało się prawdziwe, fascynuje mnie parę okoliczności.

Wacław Sierpiński polecił, by na jego grobie wyryto napis Badacz nieskończoności. André Weil, matematyk francuski, 1906-1998, założyciel i faktyczny lider tzw. grupy Bourbaki, a więc grupy odpowiedzialnej za wprowadzenie do szkół na całym świecie „nowej matematyki” lat siedemdziesiątych, powiedział, że gdyby ktoś chciał mieć jednozdaniową definicję matematyki, to należałoby powiedzieć, że jest to nauka o nieskończoności. Wyraził tym zgodną opinię, dominującą co najmniej przez trzy czwarte poprzedniego stulecia.

W -V wieku Parmenides stworzył szkołę filozoficzną, która postawiła sobie za cel zbadanie, jak ma się rozpowszechniona w tamtych czasach opinia, iż matematyka głosi najgłębszą prawdę o świecie, do rzeczywistości. Bez trudu dało się bowiem zauważyć, że pojęcia matematyki – taka, na przykład, prosta, albo – jeszcze bardziej – punkt, nijakich materialnych odpowiedników nie mają. Obiekt materialny można dzielić na mniejsze kawałki, ale przecież w końcu gdzieś będziemy musieli się zatrzymać, choćby z tego powodu, że nie można w skończonym czasie wykonać nieskończenie wielu czynności. Tymczasem matematyka pozwala choćby na odcinanie od odcinka stale połowy tego, co jeszcze zostało do dyspozycji, bez końca, a nawet pozwala stwierdzić, że w końcu z tego odcinka nic nie zostanie, nawet koniec.