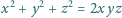Zastosujemy metodę tzw. nieskończonego schodzenia (zob. L. Kurlyandchik, Złote rybki w oceanie matematyki, TUTOR 2005).

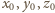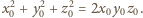Przypuśćmy przeciwnie, że to liczby całkowite dodatnie, takie że  Ponieważ prawa strona jest liczbą parzystą, to dokładnie dwie z liczb 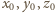są nieparzyste lub żadna nieparzysta nie jest. Pierwszy przypadek nie może mieć miejsca, gdyż wówczas lewa strona przy dzieleniu przez 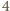dałaby resztę 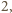 zaś prawa 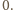 Dlatego 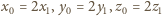dla pewnych liczb całkowitych dodatnich 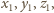 mniejszych od 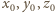odpowiednio. Po wstawieniu do równania otrzymujemy zależność 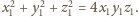 Powtarzając całe rozumowanie, dostajemy malejące ciągi liczb całkowitych dodatnich 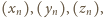 przy czym 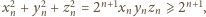 co jest niemożliwe.

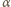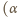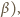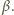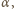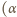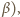Konsekwencją tak pojętego aktualizmu byłoby też odrzucenie reguły odrywania, czyli najbardziej podstawowej reguły wnioskowania, wyodrębnionej już w średniowieczu reguły modus ponens: Jeżeli prawdziwe jest zdanie oraz prawdziwa jest implikacja to to prawdziwe jest też zdanie  Można sobie przecież wyobrazić, że długość dowodu formuły  jak i długość dowodu implikacji to  są dostępnymi liczbami naturalnymi, a ich suma już nie.