Efekty nieliniowe dla rowerzystów

W matematyce często rozróżnia się rzeczy liniowe od nieliniowych. W szkole uczy się o funkcjach liniowych i nieliniowych, ale te pojęcia są dużo szersze i oprócz teorii dotyczą także wielu sytuacji praktycznych. Układ liniowy można przeanalizować w ten sposób, że rozkłada się go na części, analizuje działanie każdej z nich osobno, a na końcu dodaje do siebie poszczególne wyniki. W układzie nieliniowym taka analiza może dać niepoprawne wyniki.

Dla zilustrowania problemu zajmijmy się turystą rowerowym jadącym z prędkością 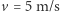$v = 5 m/s$ na letnią wycieczkę. Przy tej prędkości zazwyczaj siła oporu aerodynamicznego, wyrażająca się wzorem 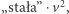$|„stała”⋅v2,$ zaczyna dominować nad wszystkimi innymi oporami ruchu - oznaczmy tę stałą przez 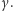$|γ.$ Ale rowerzysta na razie nie zastanawia się nad tym wszystkim. Słońce świeci, szosa jest pozioma i gładka, wiatru nie ma i jest przyjemnie.

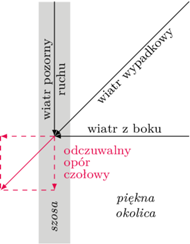
Nagle pogoda się pogarsza i prostopadle do szosy zaczyna wiać wiatr z prędkością 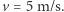$v = 5 m/s.$ Turysta myśli sobie: i co z tego, przecież wieje dokładnie z boku, może i jest mniej przyjemnie, ale to nie będzie mi przeszkadzać w jeździe. Jednak jest to błąd wywołany kontaktami z częstymi w życiu codziennym układami liniowymi, tak naprawdę wiatr będzie go całkiem znacząco hamował. To trochę zaskakujące zjawisko jest właśnie manifestacją nieliniowości układu, który tworzą rowerzysta z rowerem i powietrze.

Obliczmy siły działające na kolarza: przy bezwietrznej pogodzie siła aerodynamiczna była skierowana do tyłu i wynosiła 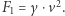$F = γ ⋅v2. 1$ Po pojawieniu się wiatru bocznego wiatr wypadkowy hamujący rowerzystę jest skierowany pod kątem 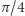$|π/4$ i ma prędkość 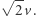$√ -- | 2v.$ Zatem siła oporu jest skierowana tak samo i ma wartość 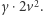$|γ⋅2v2.$ Jej składowa hamująca to 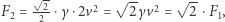$- √ -- √-- F2 = -2-⋅γ ⋅2v2 = 2γv2 = 2 ⋅F1, 2$ czyli jest o ponad 41% większa niż poprzednio. Za ten nieco deprymujący wynik odpowiedzialny jest fakt, że siła oporu aerodynamicznego nie jest liniową (w sensie szkolnym) tylko kwadratową funkcją prędkości. Niestety, wbrew swoim wyobrażeniom kolarz musi zwiększyć wysiłek, by utrzymać tę samą prędkość co poprzednio.

Wiatr z boku jest naprawdę irytujący: wszystko jedno, czy się jedzie na wakacyjny piknik, czy z niego wraca, hamuje przy jeździe w obu kierunkach. Czy nie przyjemniej byłoby w jedną stronę jechać z wiatrem, nawet jeśli w drugą będzie trochę ciężej? I to znowu jest oczekiwanie liniowego zachowania od nieliniowego układu. Znów zakładamy, że prędkość wiatru i rowerzysty jest taka sama. Obliczmy dla przykładu pracę, którą musi wykonać rowerzysta, aby pokonać opór aerodynamiczny na niedługim odcinku drogi, długości 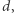$d,$ jadąc dokładnie z wiatrem i wracając dokładnie pod wiatr. Praca to iloczyn drogi i siły. Z wiatrem ta praca jest zerowa, bo nie odczuwa żadnego oporu powietrza. Pod wiatr wynosi 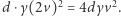$d ⋅γ(2v)2 = 4d γv2.$ Przy wietrze z boku praca jest w obie strony taka sama i łącznie wynosi 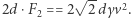$√ -- 2d ⋅F2 == 2 2dγv2.$ Zatem lepiej jest jechać, mając oba razy wiatr z boku, niż raz z wiatrem i raz pod wiatr.

Mam jeszcze jedną złą wiadomość dla naszego rowerzysty, już poza dyskusją o nieliniowości siły oporu aerodynamicznego. Stała we wzorze na tę siłę (a zatem i na pracę) zależy od powierzchni przekroju bryły stawiającej opór i jej współczynnika oporu aerodynamicznego 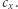$|cx.$ Tak się pechowo składa, że gdy wiatr zacznie wiać choćby trochę z boku, to wzrośnie powierzchnia stawiająca opór, bo rower z rowerzystą mają większą powierzchnię boczną niż czołową. Wzrośnie też 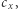$|cx,$ bo rowery są projektowane z myślą o pokonywaniu przede wszystkim oporu czołowego. Paradoksalnie, to może nawet spowodować, że w praktyce jednak lepiej będzie jechać raz z wiatrem i raz pod wiatr, niż oba razy mając go z boku. Pokazuje to, że rzeczywistość jest bardziej skomplikowana niż prosty model, który dotąd omawialiśmy.