Matematyczny kącik myzyczny
Pitagorejczycy i matematyczne początki muzyki
Jak przekazują nam starożytni, zaczęło się od przypadkowego odkrycia przypisywanego Pitagorasowi - otóż miał on spostrzec, że jeśli stosunek długości dwóch strun jest równy stosunkowi dwóch małych liczb naturalnych, to współbrzmią one harmonijnie...
Jeżeli jedna ze strun będzie dwa razy krótsza od drugiej (stosunek 2:1), to będzie brzmiała oktawę wyżej (według obecnej nomenklatury interwałów). Gdy stosunek długości wynosi 3:2, otrzymamy interwał kwinty czystej, a 4:3 - kwarty czystej. Co więcej, budując od pewnego dźwięku wpierw kwintę w górę, a od otrzymanego kwartę w górę, otrzymujemy dźwięk brzmiący oktawę wyżej od bazowego (o czym nietrudno się przekonać, mnożąc proporcje kwinty i kwarty). Jeśli natomiast wychodząc od pewnego dźwięku, zagramy dwa dźwięki odpowiednio kwartę i kwintę wyżej, to różnica pomiędzy nimi będzie całym tonem o proporcji 9:8. Półton zaś rozumiano jako pozostałość po odjęciu od kwarty dwóch całych tonów 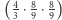 - daje to proporcję 256:243. Już starożytni byli jednak świadomi, że nie jest to dokładnie połowa całego tonu.
- daje to proporcję 256:243. Już starożytni byli jednak świadomi, że nie jest to dokładnie połowa całego tonu.

Powiązanie muzyki z liczbami - poznanie dźwięków za pomocą liczb - skłoniło Pitagorasa do odważnego twierdzenia, że wszystko jest liczbą (liczba jako 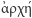 - zasada wszystkich rzeczy). Odtąd Pitagoras widział liczby we wszystkim - nie tylko w obiektach fizycznych, ale i pojęciach takich, jak sprawiedliwość czy właściwa pora. Skoro zaś pryncypia matematyki były przez Pitagorejczyków uważane za pryncypia wszystkich rzeczy, miało to istotny wpływ na rozwój tej dziedziny nauki, wspierany później przez Platona i Arystotelesa w, odpowiednio, Akademii i Lykejonie.
- zasada wszystkich rzeczy). Odtąd Pitagoras widział liczby we wszystkim - nie tylko w obiektach fizycznych, ale i pojęciach takich, jak sprawiedliwość czy właściwa pora. Skoro zaś pryncypia matematyki były przez Pitagorejczyków uważane za pryncypia wszystkich rzeczy, miało to istotny wpływ na rozwój tej dziedziny nauki, wspierany później przez Platona i Arystotelesa w, odpowiednio, Akademii i Lykejonie.
Proste interwały występują w przyrodzie
Dźwięk drgającej struny rozkłada się na szereg tzw. tonów prostych - struna drga zarówno w całej swej długości, jak i na każdej z połów, części trzecich itd. Stąd oprócz dźwięku podstawowego słyszalne są tzw. alikwoty, czyli dźwięki pozostające w stosunkach do bazowego kolejno 2:1, 3:1, 4:1 itd. Widać od razu, że kolejne alikwoty tworzą wspomniane wcześniej interwały.
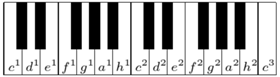
Ściągawka pianistyczna. Interwał między 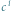 oraz
oraz 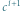 odpowiada oktawie, między
odpowiada oktawie, między 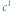 oraz
oraz 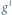 kwincie, między
kwincie, między 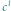 oraz
oraz 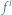 kwarcie, a między
kwarcie, a między 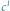 oraz
oraz 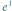 tercji wielkiej.
tercji wielkiej.
Komat pitagorejski
Wnikliwy Czytelnik zapewne zauważy, że wychodząc od pewnego dźwięku bazowego i budując od niego szereg oktaw i szereg kwint, żaden z nowo utworzonych dźwięków nie wystąpi jednocześnie w obu tych szeregach. Wynika to z prostego faktu, że nie istnieją liczby całkowite 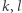 takie, że
takie, że 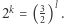 Przyglądając się jednak klawiaturze współczesnego fortepianu, dostrzeżemy, że pierwsze takie zejście następuje po 7 oktawach (12 kwintach), gdyż "pianistyczna" oktawa to odległości między 12 kolejnymi klawiszami (wliczając klawisze czarne), a "pianistyczna" kwinta to odległość między 7 klawiszami. I faktycznie, w naszych ciągach pitagorejskich interwałów w tym miejscu występuje niewielka różnica - stosunek
Przyglądając się jednak klawiaturze współczesnego fortepianu, dostrzeżemy, że pierwsze takie zejście następuje po 7 oktawach (12 kwintach), gdyż "pianistyczna" oktawa to odległości między 12 kolejnymi klawiszami (wliczając klawisze czarne), a "pianistyczna" kwinta to odległość między 7 klawiszami. I faktycznie, w naszych ciągach pitagorejskich interwałów w tym miejscu występuje niewielka różnica - stosunek 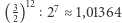 (zwany komatem pitagorejskim) stanowi niecałą
(zwany komatem pitagorejskim) stanowi niecałą 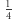 (w sensie "pierwiastek 4. stopnia") "pianistycznego" półtonu. Jest więc to różnica słyszalna. Gdybyśmy w fortepianie nastroili struny
(w sensie "pierwiastek 4. stopnia") "pianistycznego" półtonu. Jest więc to różnica słyszalna. Gdybyśmy w fortepianie nastroili struny 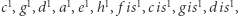
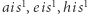 tak, by interwał między dwoma kolejnymi dźwiękami był kwintą czystą (z ewentualnym sprowadzeniem do oktawy pomiędzy
tak, by interwał między dwoma kolejnymi dźwiękami był kwintą czystą (z ewentualnym sprowadzeniem do oktawy pomiędzy 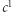 i
i 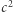 ), to okazałoby się, że dźwięk
), to okazałoby się, że dźwięk 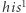 jest wyższy niż dźwięk
jest wyższy niż dźwięk 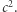
Myśląc o greckich interwałach, powinniśmy tak naprawdę zarzucić myślenie współczesną klawiaturą fortepianu, którego dźwięki stroi się inaczej - temu problemowi poświęcimy następny artykuł. Trudno powiedzieć, czy Pitagorejczycy rozważali problem instrumentu o stałym stroju, jakimi są instrumenty klawiszowe. Ówczesne instrumenty były przede wszystkim strunowe (jak np. kithara, lira czy harfa) lub dęte (najpopularniejszy był aulos, który można luźno kojarzyć z parą obojów), toteż wszelkie "niedoskonałości" wynikające ze stałego umiejscowienia otworów w piszczałce lub naciągu strun można było niwelować, nie przesłaniając do końca otworu lub palcem skracając strunę.
W ogóle Grecy mieli inne podejście do interwałów niż my współcześnie. Rozważali i stosowali takie interwały, jak 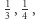
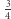 czy nawet
czy nawet 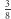 całego tonu, tworząc na ich podstawie różne rodzaje tetrachordów - sekwencji czterech dźwięków; z tetrachordów budowano następnie skale i systemy. Różnica w wielkości interwałów miała wpływ na barwę skali, przez co i charakter utworu, który był na niej oparty. Z czasem jednak niektóre z nich zanikały, lecz sama koncepcja mikrointerwałów trwała jeszcze w VII w. n.e. w monodii chorałowej, choć też powoli zanikała. Odrodziła się w muzyce na początku XX wieku.
całego tonu, tworząc na ich podstawie różne rodzaje tetrachordów - sekwencji czterech dźwięków; z tetrachordów budowano następnie skale i systemy. Różnica w wielkości interwałów miała wpływ na barwę skali, przez co i charakter utworu, który był na niej oparty. Z czasem jednak niektóre z nich zanikały, lecz sama koncepcja mikrointerwałów trwała jeszcze w VII w. n.e. w monodii chorałowej, choć też powoli zanikała. Odrodziła się w muzyce na początku XX wieku.
Na koniec pokażmy jeszcze różnicę między tercją wielką wynikającą z szeregu harmonicznego (5:4) a otrzymaną ze złożenia dwóch całych tonów 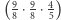 . Jest ona równa
. Jest ona równa 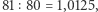 czyli nieznacznie mniejsza od komatu pitagorejskiego. Ten tzw. komat syntoniczny okazuje się być istotnym problemem, gdy w Europie rozpoczyna się operowanie trójdźwiękiem i harmonią modalną. O tym, dlaczego sprawia to kłopot i jak sobie z tym fantem radzono, opowiemy w następnym artykule.
czyli nieznacznie mniejsza od komatu pitagorejskiego. Ten tzw. komat syntoniczny okazuje się być istotnym problemem, gdy w Europie rozpoczyna się operowanie trójdźwiękiem i harmonią modalną. O tym, dlaczego sprawia to kłopot i jak sobie z tym fantem radzono, opowiemy w następnym artykule.
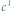 oraz
oraz 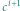 odpowiada oktawie, między
odpowiada oktawie, między 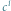 oraz
oraz 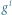 kwincie, między
kwincie, między 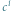 oraz
oraz 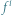 kwarcie, a między
kwarcie, a między 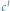 oraz
oraz 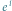 tercji wielkiej.
tercji wielkiej.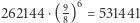 oraz że
oraz że 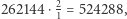 czyli interwał oktawy jest mniejszy od złożenia sześciu całych tonów (z których każdy jest złożeniem dwóch kwint pomniejszonym o oktawę).
czyli interwał oktawy jest mniejszy od złożenia sześciu całych tonów (z których każdy jest złożeniem dwóch kwint pomniejszonym o oktawę).