Matematyczne spojrzenie na reakcje chemiczne
Modelowanie matematyczne jest pewnego rodzaju sztuką opisywania świata - zarówno w skali mikro, jak i makro - za pomocą równań matematycznych (równań różniczkowych, różnicowych czy stochastycznych). Opis mikroskopowy może dotyczyć zachowania pojedynczych molekuł (cząsteczek), natomiast obiektem opisu makroskopowego jest to, co widzimy "gołym okiem", m.in. przemiany zachodzące w wyniku reakcji chemicznych. Mogą to być zmiany właściwości fizycznych danych substancji (np. stan skupienia, barwa, gęstość) lub chemicznych (np. zapach, smak, toksyczność)...
Przypomnijmy zatem, czym jest reakcja chemiczna. Jest to zachodząca w czasie przemiana jednej substancji w drugą. W wyniku reakcji chemicznej, w której bierze udział pewna substancja (zwana substratem), powstaje nowa substancja (zwana produktem), na ogół o odmiennych właściwościach fizycznych i chemicznych opisujących zachowanie wobec innych substancji. Takie przemiany zachodzą zarówno w naszym organizmie (np. trawienie pokarmów), jak i w otaczającym nas świecie (rdzewienie przedmiotów, kiszenie ogórków, pieczenie ciasta).

Reakcję chemiczną zapisujemy jako równanie chemiczne, które w przejrzysty sposób informuje nas, jakie substraty wzięły w niej udział i jaka ich ilość jest niezbędna do otrzymania danego produktu. Krótko mówiąc, jest to zapis przebiegu pewnego procesu chemicznego. Przykładem reakcji chemicznej jest synteza dwóch substratów 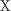 i
i 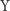 , w wyniku której powstaje produkt
, w wyniku której powstaje produkt 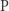 :
:

Zakładamy tutaj, że reakcja przebiega w jednym kroku, czyli że nie ma produktów pośrednich, jej szybkość opisuje parametr 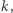 a strzałka wskazuje kierunek przebiegu reakcji. Jeśli rozważymy reakcję odwrotną (mówiąc językiem chemicznym - reakcję analizy, rozkładu), to z substancji złożonej otrzymamy co najmniej dwa produkty.
a strzałka wskazuje kierunek przebiegu reakcji. Jeśli rozważymy reakcję odwrotną (mówiąc językiem chemicznym - reakcję analizy, rozkładu), to z substancji złożonej otrzymamy co najmniej dwa produkty.
Te proste reakcje chemiczne, a dokładniej zmiany stężeń odpowiednich reagentów (czyli substratów i produktów), można zapisać w języku matematyki za pomocą równań różniczkowych zwyczajnych. Są to tzw. równania kinetyczne oparte na prawie działania mas, zwanym od nazwisk autorów - norweskich chemików, prawem Guldberga i Waagego. Prawo to mówi, że szybkość reakcji chemicznej jest proporcjonalna do iloczynu stężeń reagentów. Do opisu przemian zachodzących w czasie (np. reakcji chemicznych) matematycy wykorzystują pojęcie pochodnej, które dobrze charakteryzuje szybkość zmian pewnej wielkości, np. temperatury, ciśnienia czy nawet rozwoju choroby. Pochodna informuje, jak szybko zmienia się dana wielkość, jednocześnie umożliwiając przewidywanie zmian stężenia danej substancji czy też wzrostu liczby zachorowań na daną chorobę. Ogólnie możemy więc zapisać, że

I tak na przykład szybkość zmian w czasie stężenia substancji 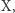 która rozpada się ze stałą prędkością
która rozpada się ze stałą prędkością 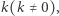 tj.
tj.

zapisujemy matematycznie (w postaci równania różniczkowego) jako

gdzie 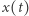 oznacza stężenie substratu w chwili
oznacza stężenie substratu w chwili 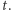 Rozwiązaniem tego równania jest funkcja
Rozwiązaniem tego równania jest funkcja

gdzie 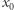 jest stężeniem początkowym. Na rysunku obok przedstawiamy rozpad w czasie substancji
jest stężeniem początkowym. Na rysunku obok przedstawiamy rozpad w czasie substancji 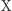 dla trzech różnych stężeń początkowych. Jak widzimy, stężenie maleje wykładniczo w czasie do
dla trzech różnych stężeń początkowych. Jak widzimy, stężenie maleje wykładniczo w czasie do 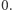
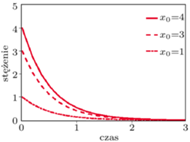
Rys. 1. Zmiany stężeń substratu 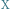 w czasie dla
w czasie dla 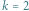
Zauważmy, że reakcję chemiczną rzędu pierwszego 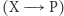 opisuje liniowe równanie różniczkowe, natomiast reakcję drugiego rzędu postaci
opisuje liniowe równanie różniczkowe, natomiast reakcję drugiego rzędu postaci 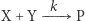 odzwierciedla układ nieliniowych równań różniczkowych
odzwierciedla układ nieliniowych równań różniczkowych
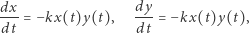 |
gdzie 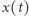 i
i 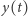 oznaczają stężenia odpowiednich substratów w chwili
oznaczają stężenia odpowiednich substratów w chwili 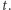
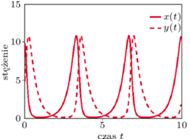
Kolejny przykład dotyczy bardziej złożonych reakcji chemicznych opisywanych za pomocą układu dwóch równań zwyczajnych. Jest to model Lotki, dzięki któremu można matematycznie wyjaśnić pojawianie się oscylacji w reakcjach chemicznych. Początkowo Alfred Lotka (1880-1949) - amerykański biofizyk, zaproponował model, w którym występowały gasnące oscylacje stężeń w czasie. Dopiero 10 lat później, tj. w roku 1920, Lotka zmodyfikował tak swój układ, aby w reakcjach chemicznych występowały oscylacje niegasnące. Opisany przez Lotkę schemat hipotetycznych reakcji chemicznych, z których każda jest nieodwracalna, ma postać

Zgodnie z prawem działania mas szybkości zmian stężeń reagentów 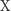 i
i 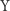 można zapisać (w języku matematyki) jako układ nieliniowych równań różniczkowych zwyczajnych
można zapisać (w języku matematyki) jako układ nieliniowych równań różniczkowych zwyczajnych
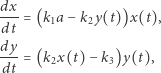 |
gdzie 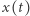 i
i 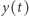 oznaczają odpowiednio stężenia reagentów
oznaczają odpowiednio stężenia reagentów 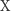 i
i 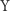 w chwili
w chwili 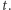 Układy autokatalityczne mogą posiadać stany stacjonarne, tj. stany, w których żadne zmienne nie ulegają zmianie pomimo upływu czasu. Matematycznie znajdujemy takie stany przez przyrównanie wszystkich pochodnych do zera i rozwiązanie odpowiednich równań algebraicznych.
Układy autokatalityczne mogą posiadać stany stacjonarne, tj. stany, w których żadne zmienne nie ulegają zmianie pomimo upływu czasu. Matematycznie znajdujemy takie stany przez przyrównanie wszystkich pochodnych do zera i rozwiązanie odpowiednich równań algebraicznych.

Rys. 2. Przykładowe pole wektorowe (u góry) oraz zmiany stężeń reagentów  i
i  w czasie
w czasie  (u dołu)
(u dołu)
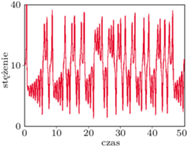
Rys. 3. Przykładowe rozwiązania chaotyczne (nieregularne)
W 1926 roku włoski matematyk Vito Volterra (1860-1940) opracował model dynamiki populacji analogiczny do modelu reakcji chemicznych (modelu Lotki). Wówczas 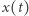 oznacza zagęszczenie ofiar (np. zajęcy) i
oznacza zagęszczenie ofiar (np. zajęcy) i 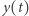 - zagęszczenie drapieżników (np. rysi), a odpowiednie reakcje chemiczne można interpretować jako
- zagęszczenie drapieżników (np. rysi), a odpowiednie reakcje chemiczne można interpretować jako

Wówczas, przyjmując 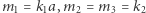 i
i 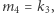 otrzymamy znany model drapieżnik-ofiara, zwany modelem Lotki-Volterry, tj.
otrzymamy znany model drapieżnik-ofiara, zwany modelem Lotki-Volterry, tj.
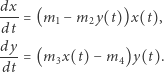 |
Badając rozwiązania układu Lotki (Lotki-Volterry), obserwujemy zachowanie oscylacyjne (wokół dodatniego stanu stacjonarnego) układu reakcji chemicznych zilustrowane na rysunku obok.
Zrozumienie struktury i mechanizmu działania reakcji chemicznych jest niezbędne do zrozumienia funkcjonowania wielu procesów biologicznych i chemicznych. Jest również konieczne do zrozumienia powstawania wielu chorób (w szczególności nowotworowych), a tym samym skutecznej walki z nimi. Poznanie mechanizmów reakcji chemicznych stanowi więc bardzo ciekawy kierunek badań, nie tylko dla chemików, ale również dla matematyków. Jednym z przykładów układu chemicznego, w którym obserwujemy bardziej skomplikowane zachowania - oscylacje chaotyczne - jest reakcja Biełousowa-Żabotyńskiego. Reakcja ta (a w zasadzie cała grupa reakcji BZ) polega na utlenianiu kwasu cytrynowego bromianem potasu w obecności katalizatora, w wyniku czego obserwuje się okresowe lub chaotyczne zmiany stężeń reagentów, co skutkuje odpowiednio regularnymi lub nieregularnymi zmianami barwy roztworu. Co ciekawe, rodzaj występującej dynamiki reakcji BZ zależy również od prędkości pompowania do reaktora odpowiednich substratów. Z kolei uwzględnienie zmian przestrzennych w reakcjach chemicznych prowadzi do równań różniczkowych cząstkowych (np. równań kinetycznych z dyfuzją), zaś opóźnienie między zainicjowaniem sprzężenia zwrotnego i jego efektem - do równań różniczkowych z opóźnieniem. A ponieważ reakcje biochemiczne często zachodzą w wyniku przypadkowych zderzeń cząsteczek reagentów, stosujemy podejście stochastyczne. Ta różnorodność narzędzi matematycznych daje możliwość lepszego poznania mechanizmów rządzących światem mikro i makro.
 w czasie dla
w czasie dla 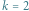
 i
i  w czasie
w czasie  (u dołu)
(u dołu)