Nieoczekiwane zastosowania szeregu harmonicznego
Problem 1. Do dyspozycji mamy nieograniczoną liczbę prostopadłościennych cegieł o jednakowym rozmiarze i masie. Cegły ustawiamy jedna na drugiej - bez użycia żadnych materiałów klejących. Jak bardzo najwyżej położona cegła może być wysunięta w stosunku do cegły położonej najniżej? Rozkład masy w każdej cegle jest jednorodny.
Problem 2. Na jednym z końców kilometrowej rozciągliwej nici siedzi mrówka. Zaczyna poruszać się ze stałą prędkością 1 cm/s w kierunku drugiego końca. Po upływie każdej sekundy nić wydłuża się o jeden kilometr - natychmiastowo i jednorodnie na całej długości. Czy mrówka jest w stanie dotrzeć na drugi koniec nici?
Zanim przedstawimy rozwiązania, przypomnijmy, że szereg harmoniczny, suma odwrotności kolejnych liczb naturalnych

jest rozbieżny, czyli jego suma jest nieskończona. Wynika to z następujących oszacowań

Rozbieżność tego szeregu odgrywa kluczową rolę w rozwiązaniach obu problemów.
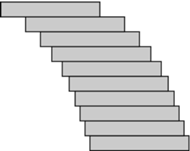
Rys. 1
Rozwiązanie problemu 1
Chcemy ustawić wieżę, której najwyższa cegła będzie wystawała możliwie daleko. Eksperymentując, na przykład z kostkami domino, możemy zauważyć, że niższe kostki warto wysunąć mniej niż te wyższe; wyższe mają "swobodę", gdyż muszą utrzymać na sobie mniej kostek (Rys. 1).
Przyjmijmy, że każda cegła ma długość 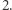 Masa cegieł jest rozłożona jednorodnie, tak że środek ciężkości znajduje się dokładnie w połowie długości cegły. Jakie wysunięcie można osiągnąć w ten sposób z czterech cegieł? Odwróćmy kolejność budowania i zacznijmy od cegły najwyższej - niech każda nowa cegła będzie dokładana na spód wieży z jej prawej strony.
Masa cegieł jest rozłożona jednorodnie, tak że środek ciężkości znajduje się dokładnie w połowie długości cegły. Jakie wysunięcie można osiągnąć w ten sposób z czterech cegieł? Odwróćmy kolejność budowania i zacznijmy od cegły najwyższej - niech każda nowa cegła będzie dokładana na spód wieży z jej prawej strony.
W środku pierwszej cegły zaczepmy poziomą oś liczbową - współrzędne środków wież będziemy obliczać względem tej osi.
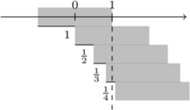
Rys. 2 Optymalna wieża z pięciu cegieł. Najwyższa cegła znajduje się w całości poza zasięgiem najniższej cegły.
Pierwsza dołożona pod spód cegła musi być ustawiona tak, by górna cegła nie wystawała o więcej niż 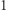 - w przeciwnym przypadku środek ciężkości górnej cegły znajdowałby się poza punktem podparcia i wieża przewróciłaby się. Jak teraz dostawić trzecią cegłę? Środek ciężkości dwóch górnych cegieł ma współrzędną
- w przeciwnym przypadku środek ciężkości górnej cegły znajdowałby się poza punktem podparcia i wieża przewróciłaby się. Jak teraz dostawić trzecią cegłę? Środek ciężkości dwóch górnych cegieł ma współrzędną 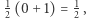 jest to współrzędna lewego końca trzeciej cegły, której środek ciężkości ma współrzędną
jest to współrzędna lewego końca trzeciej cegły, której środek ciężkości ma współrzędną 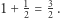
Jeszcze czwarta cegła. Środek ciężkości trzech dotychczas ustawionych cegieł ma współrzędną 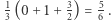 Czyli środek ciężkości czwartej cegły ma współrzędną
Czyli środek ciężkości czwartej cegły ma współrzędną 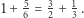 Kolejne cegły są wysunięte w prawo o
Kolejne cegły są wysunięte w prawo o 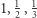 w stosunku do cegły powyżej.
w stosunku do cegły powyżej.
Ustawiajmy kolejne cegły w ten sposób i zaprzęgnijmy do pracy szereg harmoniczny. Oznaczmy przez 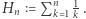 Pokażemy ogólny wzór na współrzędną lewego końca
Pokażemy ogólny wzór na współrzędną lewego końca  -tej cegły - a mianowicie jest ona równa
-tej cegły - a mianowicie jest ona równa 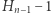 dla
dla 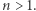 Rozumowanie poprowadzimy indukcyjnie. Przypadek, gdy
Rozumowanie poprowadzimy indukcyjnie. Przypadek, gdy 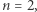 przeanalizowaliśmy powyżej, załóżmy zatem słuszność wzoru dla pewnego
przeanalizowaliśmy powyżej, załóżmy zatem słuszność wzoru dla pewnego 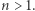
Zauważmy na początek, że środek ciężkości 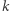 -tej cegły, dla
-tej cegły, dla 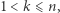 ma współrzędną równą
ma współrzędną równą 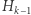 (każda cegła ma długość
(każda cegła ma długość 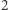 ) oraz środek ciężkości pierwszej cegły ma współrzędną równą
) oraz środek ciężkości pierwszej cegły ma współrzędną równą 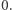 Tym samym środek ciężkości wszystkich
Tym samym środek ciężkości wszystkich  cegieł ma współrzędną równą
cegieł ma współrzędną równą

gdzie równość 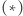 uzasadniona jest na marginesie. Pamiętając, że środek ciężkości
uzasadniona jest na marginesie. Pamiętając, że środek ciężkości 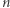 cegieł wyznacza położenie lewego końca cegły
cegieł wyznacza położenie lewego końca cegły 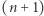 -wszej, otrzymujemy tezę.
-wszej, otrzymujemy tezę.
Podsumujmy: prawy brzeg najwyższej cegły ma współrzędną 1, lewy koniec każdej kolejnej cegły ma współrzędną równą 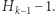 W szczególności możliwe jest ustawienie takiej wieży, żeby wysunięcie było równe jednej, dwóm lub dziesięciu długościom cegły. W teorii wysunięcie może być dowolnie duże. Wysunięcie większe niż 1 uzyskamy już dla 5 cegieł (Rys. 2), długości 2 dla 32 cegieł, długości 3 dla 228 cegieł. Ile cegieł jest potrzebnych do wysunięcia długości 4?
W szczególności możliwe jest ustawienie takiej wieży, żeby wysunięcie było równe jednej, dwóm lub dziesięciu długościom cegły. W teorii wysunięcie może być dowolnie duże. Wysunięcie większe niż 1 uzyskamy już dla 5 cegieł (Rys. 2), długości 2 dla 32 cegieł, długości 3 dla 228 cegieł. Ile cegieł jest potrzebnych do wysunięcia długości 4?
Rozwiązanie problemu 2
Rozważmy ogólniejszy problem:  to początkowa długość nici;
to początkowa długość nici; 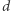 - każdorazowe wydłużenie nici;
- każdorazowe wydłużenie nici;  - dystans pokonywany przez mrówkę w ciągu każdej sekundy (między wydłużeniem nici). Zobaczmy, co stanie się w pierwszej sekundzie: mrówka pokonała
- dystans pokonywany przez mrówkę w ciągu każdej sekundy (między wydłużeniem nici). Zobaczmy, co stanie się w pierwszej sekundzie: mrówka pokonała 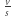 części całej nici, która rozciąga się następnie jednorodnie. Po tym rozciągnięciu mrówka nadal ma za sobą taką samą część całej nici. W drugiej sekundzie sytuacja jest podobna - mrówka pokona
części całej nici, która rozciąga się następnie jednorodnie. Po tym rozciągnięciu mrówka nadal ma za sobą taką samą część całej nici. W drugiej sekundzie sytuacja jest podobna - mrówka pokona 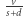 części nici (o długości
części nici (o długości 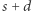 ), a więc łącznie pokona
), a więc łącznie pokona 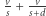 całej drogi. Zauważmy, że proces rozciągania nie wpływa na to, w jakiej części nici znajduje się mrówka. Po trzeciej sekundzie mrówka pokona
całej drogi. Zauważmy, że proces rozciągania nie wpływa na to, w jakiej części nici znajduje się mrówka. Po trzeciej sekundzie mrówka pokona 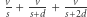 nici. Niech funkcja
nici. Niech funkcja 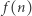 określa część nici przebytą w czasie
określa część nici przebytą w czasie  sekund (przed rozciągnięciem). Możemy stwierdzić, że
sekund (przed rozciągnięciem). Możemy stwierdzić, że

Zauważamy jednak, że dla 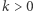 zachodzi
zachodzi 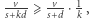 stąd
stąd

Ponieważ 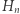 jest rozbieżny, to istnieje takie
jest rozbieżny, to istnieje takie 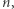 dla którego
dla którego 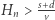 ; dla takiego
; dla takiego  otrzymujemy
otrzymujemy 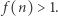 A to oznacza, że mrówka dotarła na drugi koniec nici!
A to oznacza, że mrówka dotarła na drugi koniec nici!

Zauważmy rzecz niezwykłą - niezależnie od wyboru wartości 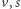 oraz
oraz 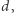 mrówka ostatecznie zawsze pokona cały dystans. Potrzebne jest jednak robocze założenie, że mrówka jest nieśmiertelna. Aby się przekonać dlaczego, odpowiedzmy na pytanie: jak długo mrówka będzie musiała kroczyć, aby osiągnąć swój cel? Otóż ma miejsce następujące przybliżenie
mrówka ostatecznie zawsze pokona cały dystans. Potrzebne jest jednak robocze założenie, że mrówka jest nieśmiertelna. Aby się przekonać dlaczego, odpowiedzmy na pytanie: jak długo mrówka będzie musiała kroczyć, aby osiągnąć swój cel? Otóż ma miejsce następujące przybliżenie

Po przekształceniach otrzymujemy jawny wzór na 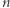 - przybliżony czas marszu mrówki wynosi
- przybliżony czas marszu mrówki wynosi

W szczególności, dla danych opisanych w naszym problemie otrzymujemy 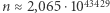 sekund. To duża (!) liczba - szacowany wiek Wszechświata to około
sekund. To duża (!) liczba - szacowany wiek Wszechświata to około 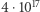 sekund.
sekund.
Problem 2 można uogólnić na przypadek, w którym nie tylko mrówka porusza się ze stałą prędkością, ale również nić rozciąga się stale (tj. w każdej chwili ze stałą prędkością). Innymi słowy - przypadek dyskretny omówiony powyżej zamieniamy na problem z czasem ciągłym. Przy czym ostrzegamy: do rozwiązania użyjemy równania różniczkowego. (Problem 2 oraz jego wariant wydają się sprzeczne z intuicją i z tego powodu często określa się je mianem paradoksu - jest on zbliżony w swojej naturze do paradoksu Achillesa i żółwia.)
Rozwiązanie problemu 2'
Niech 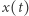 oznacza pozycję mrówki w chwili
oznacza pozycję mrówki w chwili 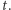 Nić zaczepiamy na osi liczbowej tak, że jej nieruchomy koniec jest w punkcie
Nić zaczepiamy na osi liczbowej tak, że jej nieruchomy koniec jest w punkcie 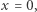 drugi zaś koniec przesuwa się wzdłuż dodatniej półosi. Prędkość, z jaką porusza się mrówka, jest równa
drugi zaś koniec przesuwa się wzdłuż dodatniej półosi. Prędkość, z jaką porusza się mrówka, jest równa  powiększonemu o bieżącą prędkość, z jaką rozciąga się dany kawałek nici. Aktualna długość nici to
powiększonemu o bieżącą prędkość, z jaką rozciąga się dany kawałek nici. Aktualna długość nici to 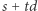 i tylko drugi koniec porusza się z prędkością
i tylko drugi koniec porusza się z prędkością 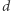 - punkt odległy o
- punkt odległy o 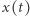 od punktu początkowego mrówki porusza się z prędkością
od punktu początkowego mrówki porusza się z prędkością 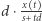 proporcjonalną do położenia na nici. Równanie różniczkowe (ostrzegaliśmy) opisujące taką sytuację:
proporcjonalną do położenia na nici. Równanie różniczkowe (ostrzegaliśmy) opisujące taką sytuację:

Rozwiązaniem tego równania jest funkcja

gdzie 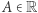 jest pewną nieznaną stałą. Wyznaczamy ją przez uwzględnienie warunku
jest pewną nieznaną stałą. Wyznaczamy ją przez uwzględnienie warunku 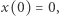 który znajduje się w opisie problemu. Otrzymujemy
który znajduje się w opisie problemu. Otrzymujemy 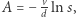 a tym samym
a tym samym

Rozwiązanie problemu polega teraz na znalezieniu takiego 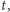 dla którego
dla którego 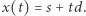 Korzystając z wyprowadzonego przed chwilą wzoru, możemy wykazać, że
Korzystając z wyprowadzonego przed chwilą wzoru, możemy wykazać, że

Oznacza to w szczególności, że dla dowolnego 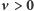 oraz dowolnych
oraz dowolnych 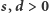 mrówka zawsze dotrze na koniec nici. Jeżeli
mrówka zawsze dotrze na koniec nici. Jeżeli 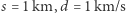 oraz
oraz 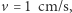 to
to 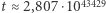 sekund. Jest to wynik bardzo zbliżony do tego otrzymanego w przypadku dyskretnym. Co więcej, można zauważyć spore podobieństwo w otrzymanych wzorach przybliżających czas wędrówki.
sekund. Jest to wynik bardzo zbliżony do tego otrzymanego w przypadku dyskretnym. Co więcej, można zauważyć spore podobieństwo w otrzymanych wzorach przybliżających czas wędrówki.
Zostawmy chwilowo szereg harmoniczny i przyjrzyjmy się ekspansji Wszechświata. Współczesny model kosmologiczny bazuje na dwóch kluczowych obserwacjach:
- obiekty odległe od Ziemi oddalają się od niej,
- tempo oddalania jest proporcjonalne do odległości od Ziemi.
Te obserwacje to tak zwane prawo Hubble'a. Taki model Wszechświata jest zbliżony w opisie do Problemu 2 (również 2') - Wszechświatem jest nić, a jego ekspansja to jej rozciąganie. Zauważmy, że w modelu z nicią tempo rozciągania było proporcjonalne do odległości od jednego z końców nici (tego, z którego zaczynała swój marsz mrówka) - odpowiada to dokładnie prawu Hubble'a. Co w szczególności wynika z rozwiązania problemów 2 i 2' dla podboju Wszechświata? Nie musimy przejmować się tym, że dalsze punkty uniwersum oddalają się coraz szybciej. Mając do dyspozycji odpowiedni statek i dużo czasu, możemy dotrzeć do dowolnego punktu w obserwowalnym kosmosie.
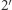 jest typu Lagrange'a-d'Alemberta i jego (dość skomplikowane) rozwiązanie pomijamy.
jest typu Lagrange'a-d'Alemberta i jego (dość skomplikowane) rozwiązanie pomijamy.