Zagadnienie jest znane w kręgach matematycznych jako problem sekretarki. Nie wiadomo, kto i kiedy jako pierwszy sformułował tę zagadkę, ale swoją popularność zyskała w 1960 roku po publikacji lutowego numeru czasopisma Scientific American. Oryginalnie problem był postawiony w następujący sposób: szef biura pilnie potrzebuje sekretarki, w związku z czym ogłasza nabór na to stanowisko. Na ogłoszenie odpowiada 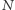kandydatek, z którymi szef przeprowadza rozmowy kwalifikacyjne. Po każdym wywiadzie rekruter ma dwie opcje: przyjąć kandydatkę i tym samym zakończyć poszukiwania bądź odmówić rekrutowanej osobie i zaprosić następną kandydatkę. Zakładamy, że (np. z racji dużego ruchu na rynku pracy) nie ma możliwości zmiany raz podjętej decyzji. Kiedy jest najlepszy moment na zakończenie rekrutacji, jeśli celem jest wybranie najlepszej kandydatki spośród wszystkich 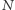zgłoszonych?

Intuicyjnie wiemy, że decyzji nie należy podejmować zbyt szybko (wówczas jest duża szansa, że nigdy nie spotkamy najlepszej kandydatki), ani zwlekać zbyt długo (najlepszą kandydatkę możemy wówczas pochopnie odrzucić). Okazuje się, że najbardziej opłaca się szukać właściwej kandydatki dopiero po przesłuchaniu około 37% kandydatek. Skąd akurat taka liczba? Można zauważyć, że najkorzystniejsza strategia polega na podzieleniu rekrutacji na dwie fazy. Najpierw należy zorientować się w kwestii ogólnego poziomu kandydatek, tj. istnieje taka liczba osób 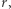których aplikacje należy z automatu odrzucić, a same rozmowy kwalifikacyjne traktować jako zbieranie informacji (oczywiście musi być 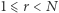). Po przeprowadzeniu wywiadów (pula testowa), w drugiej fazie należy wybrać pierwszą kandydatkę, która będzie lepsza od najlepszej z puli testowej. Jakie (w wersji asymptotycznej: jaki stosunek 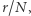gdy 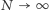) da nam największe prawdopodobieństwo wybrania najlepszej sekretarki z całej puli? Zauważmy, że w puli zasadniczej jest 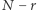kandydatek. Wyżej postawiony problem, z matematycznego punktu widzenia, sprowadza się do znalezienia takiego 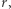dla którego pewien ciąg liczbowy osiąga maksimum. Rozważmy przypadek, gdy najlepsza kandydatka jest na pozycji 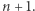W oczywisty sposób, jeśli 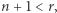to nie jesteśmy w stanie jej znaleźć. Schemat poniżej ilustruje przypadek, gdy najbardziej kompetentna osoba jest w puli zasadniczej.

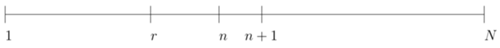
Aby najlepsza kandydatka została faktycznie wybrana, musi zajść następujące zdarzenie: najlepsza kandydatka w jest również najlepsza w (którego prawdopodobieństwo oczywiście wynosi 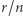). Ten warunek gwarantuje wytrwanie procesu rekrutacji do rozmowy z kandydatką 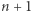(czyli najlepszą z całej grupy 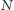osób). Teraz, aby określić prawdopodobieństwo całkowite sukcesu, sumujemy odpowiednie prawdopodobieństwa warunkowe, przy kolejnych założeniach, że najlepsza kandydatka zajmuje pozycję 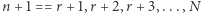(przemnożone przez prawdopodobieństwa warunków, które w tym problemie stale wynoszą ):

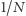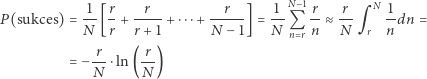
gdzie 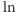jest oznaczeniem logarytmu naturalnego. Teraz wystarczy znaleźć maksimum wyrażenia na 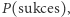aby ustalić optymalny stosunek 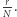(Szukanie maksimum z użyciem pochodnej przyrównanej do zera - na marginesie.) Z naszych rozważań wynika, że wynosi on 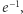czyli że pula testowa kandydatek powinna zawierać 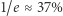wszystkich kandydatek. Wówczas szansa na znalezienie najlepszej osoby na stanowisko sekretarki wynosi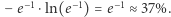

W literaturze można spotkać się z różnymi modyfikacjami problemu sekretarki. Wynik będzie inny, jeśli możemy wrócić do początkowo odrzuconych osób albo zadowolimy się najlepszą lub prawie najlepszą kandydatką. Warto zauważyć, że tę matematyczną zagadkę można również rozważyć w sposób czasowy, nie ilościowy. Jeśli na przykład nabór na stanowisko sekretarki trwa dokładnie miesiąc, a nie wiemy, ile dostaniemy CV, to optymalną pulą testową będzie pierwsze 11 dni ( 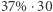dni), niezależnie od ilości rozmów kwalifikacyjnych. Następnie powinniśmy zatrudnić pierwszą osobę lepszą od osób z puli testowej.

Problem sekretarki dzięki swojej prostocie i jednoznacznemu rozwiązaniu znajduje zastosowanie w wielu dziedzinach życia, także codziennego. Matematyka podpowiada, że powinniśmy postępować zgodnie z regułą 37%, jeśli chodzi np. o wynajem mieszkania. Przeprowadzając się do nowego miasta (np. z powodu wyjazdu na studia), najczęściej nie mamy wiedzy, jaki jest tam rynek nieruchomości. Jeżeli szukamy mieszkania do wynajęcia, warto ustalić sobie limit, np. 30 potencjalnie interesujących lokali, z czego pierwsze 11 potraktować jako wstępne oględziny rynku nieruchomości. Podobnie rzecz ma się z randkami i ślubami, które także można sprowadzić do problemu sekretarki. Umawianie się za pośrednictwem portali randkowych niekiedy przypomina rozmowy rekrutacyjne. Z puli interesujących nas współużytkowników portalu staramy się wybrać "tę najlepszą" lub "tego najlepszego". Schemat postępowania powinien być podobny: ustalić liczbę spotkań, na jakie jesteśmy gotowi, pierwsze 37% potraktować wyłącznie jako zbieranie informacji, a z puli pozostałych osób wybrać pierwszą lepszą niż kandydaci/-tki z puli testowej.

W przypadku bardziej poważnych decyzji, takich jak ślub i ustatkowanie się, także możemy zrobić użytek z problemu sekretarki. Zauważmy, że nie jesteśmy w stanie oszacować, ilu potencjalnych partnerów spotkamy w życiu. W takim przypadku lepiej jest się odnieść do limitu czasowego: z przyczyn biologicznych i prawnych najlepszym czasem na założenie rodziny jest wiek między 18 a 35 lat. Mamy więc w sumie 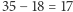lat na zbieranie informacji i podjęcie decyzji o ustatkowaniu się. Z powyższych rozważań wiemy już, że przez pierwsze 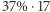lat 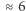lat powinniśmy poświęcić wyłącznie gromadzeniu danych. W wieku ok. 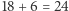lat przychodzi moment, gdy musimy być gotowi na podjęcie ostatecznej decyzji.

Problem sekretarki był wielokrotnie testowany na ochotnikach podczas badań psychologicznych i behawiorystycznych. Naukowcy chcieli sprawdzić, czy ludzie intuicyjnie skłaniają się ku zasadzie 37%. Okazuje się, że nie. Z badań wynika, że rodzaj ludzki jest raczej niecierpliwy i przystępuje do podejmowania decyzji już po ok. 31% puli. Na zbyt szybkim podejmowaniu decyzji można stracić, np. gdy na wycieczce szukamy kawiarni. Przedwczesne zdecydowanie się na filiżankę cappuccino może sprawić, że bezsensownie przepłacimy, podczas gdy tańsza kawiarnia jest tuż za rogiem. O ile zapłacenie zbyt wiele za kawę nie jest tragedią, o tyle w przypadku sprzedaży domu czy zamążpójścia zbyt szybko podjęta decyzja może być brzemienna w skutkach. Warto o tym pamiętać, kiedy następnym razem będziemy podejmować decyzję, i być może powstrzymać się przed zbyt szybkim i pochopnym przerwaniem poszukiwań.

Autorka zaznacza, że powyższe rozważania są jedynie ciekawostką matematyczną, nieuwzględniającą wszystkich możliwych scenariuszy i parametrów związanych z prawdziwym życiem. Ostatecznie, jak zauważył Mark Twain: "Są trzy rodzaje kłamstw: kłamstwa, bezczelne kłamstwa i statystyki".

Więcej o informatycznych algorytmach i ich odniesieniu do codziennego życia można przeczytać w książce Algorytmy. Kiedy mniej myśleć autorstwa Toma Griffithsa i Briana Christiana.