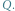Trzy spojrzenia na teorię gier

W dniach 9-21 września 2018 r. odbyła się trzecia edycja międzynarodowego obozu Maths Beyond Limits . 60 uczestników z Białorusi, Belgii, Czech, Danii, Estonii, Norwegii, Polski, Rumunii, Słowacji, Szwecji, Ukrainy i Węgier wzięło udział w warsztatach matematycznych prowadzonych przez studentów i pracowników naukowych polskich i zagranicznych uczelni. Mieli oni także okazję do zaprezentowania własnych referatów oraz do uczestnictwa w ogólnorozwojowych zajęciach wieczornych. Ponadto, w czasie obozu odbyły się: mecz matematyczny, zawody Relays (oparte na konkursie Náboj), Puzzle Hunt, a także zajęcia sportowe i integracyjne.

Spojrzenie I - opisowe

Gry, którymi będziemy się zajmować, z pozoru wydają się dosyć nietypowe - nie ma w nich wygranych ani przegranych, a wszyscy gracze wykonują swoje ruchy jednocześnie. Okazuje się jednak, że nawet bardzo uproszczone gry tego rodzaju mogą przedstawiać sytuacje praktyczne - a co dopiero ich bardziej skomplikowane wersje.

Przez grę rozumiemy sytuację, w której istnieje pewna skończona liczba graczy i jedynym celem każdego z nich jest zmaksymalizowanie swojej wypłaty (wyrażonej np. w zarobionych pieniądzach, zaoszczędzonym czasie itd.). Rozgrywka polega na jednoczesnym wybraniu przez każdego gracza strategii (każdy gracz ma swój własny, być może zupełnie unikalny, zestaw możliwych strategii). Następnie gracze otrzymują wypłaty, których wielkość zależy tylko od strategii wybranych przez poszczególnych graczy (zależność wysokości wypłat od strategii jest znana jeszcze przed rozgrywką).

Tabela przedstawia wypłaty graczy. Wiersze to strategie gracza 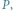$P, |$ a kolumny to strategie gracza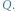 $|Q.$

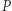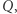Przykładem takiej gry może być następująca uproszczona sytuacja: dwie firmy, $|P$ i $Q,$ sprzedają ten sam produkt. Każda z nich ma do wyboru 2 strategie reklamowe: A i B. Jeśli obie zdecydują się na A, zarobią po 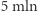$5 | mln$ złotych, jeśli obie wybiorą strategię B - po 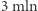$3 mln$ złotych. Jeśli jedna z nich wybierze strategię A, a druga B, to firma, która wybrała strategię B zarobi 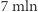$|7 mln$ złotych, podczas gdy ta druga - tylko 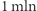$|1 mln$ złotych. Możemy wytłumaczyć taki rozkład w ten sposób, że strategia B jest nieco bardziej kontrowersyjna od A - jeśli tylko jedna firma ją zastosuje, wyróżni się, zdobywając klientów. Natomiast jeśli obie ją zastosują, konsumenci poczują się przytłoczeni i nie będą skłonni skorzystać z usług żadnej firmy.

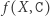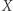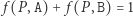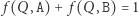Jednak w rzeczywistości gracze zwykle nie muszą ograniczać się tylko do tych dwóch opcji. Każda z firm mogłaby przecież przeznaczyć pewną część swoich środków na realizację strategii A, zaś część na realizację strategii B. Jeśli przez $,C) | f(X$ oznaczymy nieujemną część środków przeznaczoną przez gracza $X$ na realizację strategii C (oczywiście zachodzi $| f(P,A) + f(P,B) = 1$ i $,A)+ f(Q,B)=1 | f(Q$ ), to wtedy firma 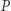$P$ dostałaby wypłatę wynoszącą

$,A)+1 f(P,A) f(Q,B)+ 5 f(P,A) f (Q ,A)+3 f(P,B) f(Q,B). +7 f(P ,B) f(Q$

Powyższe przybliża nas do sensu pojęcia strategii mieszanej. Dla danego gracza, mającego możliwość zagrania jednej z

d

strategii, strategią mieszaną nazywamy ciąg liczb

|x1,...,xd,

z których każda wyraża, jaką część swoich środków ten gracz przeznacza na zagranie odpowiedniej strategii. Liczby te muszą być nieujemne i sumować się do

|1

(w sumie należy przeznaczyć całość środków). W takim przypadku, jeśli

|wi

oznacza, jak dużą wypłatę otrzyma nasz gracz, zużywając wszystkie swoje środki na

i |

-tą strategię (przyjmujemy, że pozostali gracze już wybrali strategie), to jego wypłata w przypadku zagrania strategii mieszanej wyniesie:

d |P i 1xiwi.

W rzeczywistości firmy mają swoje strategie i raczej nie zdarza się, by co chwilę zmieniały długoletni plan działania. Po wielu analizach i eksperymentach dochodzą do wniosku, że ich system jest optymalny przy aktualnej koniunkturze na rynku i raczej nie warto odstępować od pierwotnych założeń. Spojrzenie matematyczne pozwoli nam zrozumieć, dlaczego tak jest.

Spojrzenie II - matematyczne

Równowagą Nasha nazwiemy takie przyporządkowanie strategii (być może mieszanych) każdemu graczowi, że żaden z nich, jeśli jako jedyny zmieni swoją strategię, nie zwiększy swojej wypłaty. Okazuje się, że potrafimy udowodnić istnienie takiej równowagi we wspomnianych grach.

Twierdzenie (o istnieniu równowagi Nasha). W każdej grze, w której liczba graczy jest skończona i każdy gracz ma skończoną liczbę czystych strategii, istnieje równowaga Nasha (być może złożona ze strategii mieszanych).

Dowód. Niech 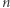$n |$ oznacza liczbę graczy, 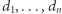$d1,...,dn$ liczbę czystych strategii dla poszczególnych graczy oraz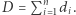 $=Pni1di. D$

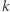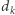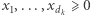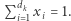Krok 1. Przekształćmy twierdzenie do postaci geometrycznej. Możliwe ruchy $|k$ -tego gracza można przedstawić jako zbiór takich punktów przestrzeni $|d k$ -wymiarowej, że: $x ,...,x ⩾ 0 1 dk$ oraz $| dk x = 1. P i 1 i$ Oznaczmy otrzymaną figurę przez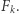 $Fk.$

Połączmy figury 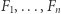$F ,...,F 1 n$ w jedną, aby móc geometrycznie przedstawiać kombinacje ruchów wszystkich graczy. Potrzebujemy do tego przestrzeni 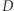$|D$ -wymiarowej. Punkt o współrzędnych 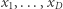$x1,...,xD$ należy odczytywać po kolei - tj. pierwszych 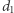$d1$ współrzędnych mówi, jaką strategię mieszaną wybrał pierwszy z graczy, kolejne 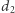$d 2$ współrzędnych mówi o decyzji drugiego gracza itd. 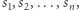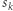W skrócie będziemy zapisywać $s1,s2,...,sn,$ gdzie $sk$ oznacza strategię (być może mieszaną) gracza 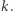$k.$ Oznaczmy figurę złożoną z takich punktów przez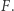 $|F.$

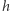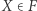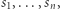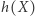Zastanówmy się, czym w tym nowym wyobrażeniu jest poszukiwany punkt równowagi. Zdefiniujemy funkcję zmiany zdania $|h$ : jeśli $∈F |X$ odpowiada wyborowi przez graczy strategii mieszanych $s1,...,sn,$ to $) h(X$ jest zbiorem kombinacji takich strategii mieszanych 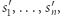$s′1,...,s′n,$ że dla gracza 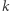$|k$ optymalną reakcją (tj. maksymalizującą jego wypłatę) na wybranie przez innych graczy strategii 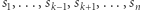$s ,...,s ,s ,...,s 1 k−1 k+1 n$ jest zagranie strategii 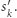$s′. k$ Z tej definicji funkcji 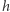$|h$ wynika, że punkt 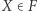$∈F |X$ jest punktem równowagi Nasha wtedy, gdy 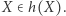$∈h(X).X$ Dla funkcji, której wartościami są podzbiory dziedziny, warunek ten jest definicją punktu stałego.

Krok 2. Zbadajmy własności figury 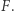$F.$ Okazuje się, że jest ona ograniczona, wypukła i domknięta. Udowodnienie tych trzech własności pozostawiamy Czytelnikowi Dociekliwemu. Podpowiemy, że wystarczy udowodnić te własności dla składników figury 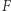$|F$ - tj. figur 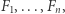$|F1,...,Fn,$ obrazujących możliwe strategie mieszane poszczególnych graczy.

Krok 3. Przypomnijmy twierdzenie Brouwera:

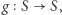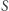Twierdzenie. Każda funkcja ciągła $g S S,$ gdzie $|S$ jest figurą wypukłą i zwartą (tj. ograniczoną i domkniętą) ma punkt stały.

Chciałoby się zastosować to twierdzenie do funkcji 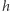$h$ ; niestety, nie jest to możliwe, gdyż jej wartościami są podzbiory (nie elementy) dziedziny. Szczęśliwie, dla takich wyszukanych funkcji istnieje odpowiednik twierdzenia Brouwera - jest to twierdzenie Kakutaniego, a jego założenia (których tu nie przytoczymy) są w naszym przypadku spełnione. Zastosowanie tego twierdzenia kończy dowód - wspomnieliśmy już, że szukany punkt stały jest punktem równowagi Nasha w rozpatrywanej grze.

Zachęcamy Czytelnika do spróbowania swoich sił z następującymi zadaniami:

(1): Znaleźć równowagi Nasha dla gry wspomnianej na początku artykułu.
(2): Rozważyć, czy zawsze istnieje równowaga Nasha składająca się wyłącznie ze strategii czystych.

Spojrzenie III - praktyczne

Noblista w dziedzinie ekonomii, Robert Aumann powiedział, że "Wszystko, co się dzieje na świecie, jest grą. Od ewolucji po wojny". Każda podjęta przez nas decyzja czyni nas graczem: wybór firmy, której produkt kupimy, przejście przez pasy na czerwonym lub zielonym świetle lub nawet wybór sposobu i towarzystwa do spędzenia wolnego czasu.

Dobrym tego przykładem jest działanie kartelu naftowego - OPEC. Członkowie OPEC stają przed dylematem: ograniczyć wydobycie ropy lub wydobywać jej tyle, ile są w stanie. Najlepszą opcją dla wszystkich jest ograniczenie nieco wydobycia, aby ceny wzrosły. W wyniku tego wszyscy członkowie zwiększą swoje zyski w porównaniu do nieograniczonego wydobycia i sprzedawania ropy za niższą cenę. Jednak z drugiej strony, każdemu członkowi opłaca się sprzedawać jak najwięcej swoich zapasów ropy naftowej, zyskując na dodatkowej sprzedaży. W takim razie: czy zmniejszyć wydobycie, trzymając się ustaleń, czy też tego nie robić? Odejście od współpracy zawsze wydaje się lepszą opcją, ponieważ wtedy gracz, który odstąpił sprzedaje więcej ropy po tej samej cenie. Z drugiej jednak strony, jeśli większość członków wybierze tę opcję, ceny spadną i finalnie wszyscy członkowie kartelu zarobią mniej, niż w przypadku trzymania się ograniczeń przez wszystkich.

Kolejnym przykładem gry, w której gracze postawili na indywidualne korzyści zamiast współpracy, jest zimna wojna. Podczas niej NATO i Układ Warszawski miały do wyboru zbrojenie się lub zaprzestanie tego. Z punktu widzenia każdej ze stron, zaprzestanie zbrojenia, podczas gdy przeciwnik nadal się zbroi, doprowadziłoby do militarnej niższości i możliwej zagłady. Odwrotnie, zbrojenie się, podczas gdy przeciwnik tego nie robił, dawało militarną przewagę. Jeśli obie strony ciągle by się zbroiły, obie ponosiłyby wysokie koszty produkcji i utrzymania arsenału nuklearnego - z drugiej strony ze względu na brak znaczącej przewagi militarnej nie powinny się atakować. Gdyby obie strony zdecydowały się rozbroić, nie byłoby takich kosztów. Na tym polega paradoksalność równowagi Nasha - chociaż obie strony ekonomicznie najlepiej wychodzą na rozwiązaniu pokojowym, to jednak najlepszym dla nich wyborem jest zbrojenie się, właśnie tak, jak miało to miejsce podczas zimnej wojny. Obie strony wkładały ogromne pieniądze w badania wojskowe, budowę i utrzymanie arsenału przez 30 lat, aż do momentu, kiedy gospodarka Związku Radzieckiego była już zbyt niewydolna, aby kontynuować ten proces.