Problem samotnego kolarza
Na torze w kształcie okręgu o obwodzie jednostkowym ściga się 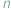 kolarzy. Każdy pędzi z inną, ale stałą prędkością. Wystartowali z tego samego punktu, jadą w tym samym kierunku. Jest ciemno, nic nie widać, choć oko wykol...
kolarzy. Każdy pędzi z inną, ale stałą prędkością. Wystartowali z tego samego punktu, jadą w tym samym kierunku. Jest ciemno, nic nie widać, choć oko wykol...
Każdy kolarz ma w rowerze włączoną lampę przednią, która oświetla otwarty łuk toru długości 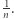 Kolarz jest samotny, jeżeli w pewnej chwili nie widzi przed sobą nikogo ani nikt inny nie oświetla go z tyłu.
Kolarz jest samotny, jeżeli w pewnej chwili nie widzi przed sobą nikogo ani nikt inny nie oświetla go z tyłu.
Tę melancholijną hipotezę postawił Jörg Michael Wills w roku 1967, w kontekście aproksymacji diofantycznych. Dla 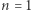 jest ona trywialnie prawdziwa. Dla
jest ona trywialnie prawdziwa. Dla 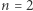 jest niemal oczywista: w pewnym momencie dwaj kolarze pędzący z różnymi prędkościami muszą znaleźć się na końcach średnicy toru, wtedy obydwaj staną się samotni. Ale dla
jest niemal oczywista: w pewnym momencie dwaj kolarze pędzący z różnymi prędkościami muszą znaleźć się na końcach średnicy toru, wtedy obydwaj staną się samotni. Ale dla 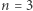 zadanie nie jest już całkiem banalne (zachęcamy Czytelnika do przeprowadzenia ścisłego dowodu hipotezy). Do dzisiaj hipoteza została potwierdzona jeszcze dla
zadanie nie jest już całkiem banalne (zachęcamy Czytelnika do przeprowadzenia ścisłego dowodu hipotezy). Do dzisiaj hipoteza została potwierdzona jeszcze dla 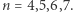 Stopień komplikacji w kolejnych przypadkach rośnie, np. dowód hipotezy dla sześciu kolarzy rozciąga się na niemal pięćdziesięciu stronach wydruku.
Stopień komplikacji w kolejnych przypadkach rośnie, np. dowód hipotezy dla sześciu kolarzy rozciąga się na niemal pięćdziesięciu stronach wydruku.
Co tedy robić? George Pólya radzi:
Dla każdego problemu, którego nie potrafisz rozwiązać, istnieje łatwiejszy problem, którego też nie będziesz potrafił rozwiązać. Znajdź go.
Może osłabić lampy w rowerach? Nietrudno dowieść, że przy lampach o zasięgu dwukrotnie mniejszym hipoteza jest prawdziwa. Najpierw zauważmy, że nie tracimy ogólności przy zmniejszeniu lub zwiększeniu wszystkich prędkości o tę samą wartość. Możemy zatem przyjąć, że jeden z kolarzy, dowolnie wybrany, pędzi z prędkością zero, czyli właściwie stoi w punkcie startu. Po wyzerowaniu wybranego kolarza mogą się pojawić kolarze z ujemnymi prędkościami, czyli jadący do tyłu. Tych należy zastąpić jadącymi w tym samym tempie do przodu. Zabieg ten nie ma znaczenia dla samotności stojącego kolarza.
To rozumowanie prowadzi do nieco innego, acz równoważnego sformułowania wyjściowego problemu. Przypuśćmy, że w punkcie startu kolarzy stoi lampa oświetlająca łuk otwarty o rozpiętości 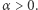 Kolarze jadą z prędkościami dodatnimi w tym samym kierunku. Lampy w rowerach są wygaszone. Czekamy na moment, w którym żadnego kolarza nie będzie w oświetlonym łuku. Przy założeniu, że ściga się
Kolarze jadą z prędkościami dodatnimi w tym samym kierunku. Lampy w rowerach są wygaszone. Czekamy na moment, w którym żadnego kolarza nie będzie w oświetlonym łuku. Przy założeniu, że ściga się 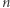 kolarzy i
kolarzy i 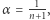 Hipoteza 1 może być sformułowana w jeszcze bardziej posępny, ale równoważny, sposób.
Hipoteza 1 może być sformułowana w jeszcze bardziej posępny, ale równoważny, sposób.

Obliczymy teraz, jak długo pojedynczy kolarz przebywa w oświetlonym łuku podczas całego wyścigu. Niech  będzie liczbą całkowitą dodatnią wyrażającą prędkość kolarza (nietrudno uzasadnić, że ograniczenie do liczb całkowitych nie zmniejsza ogólności zagadnienia). Przyjmijmy zatem, że kolarz pokonuje
będzie liczbą całkowitą dodatnią wyrażającą prędkość kolarza (nietrudno uzasadnić, że ograniczenie do liczb całkowitych nie zmniejsza ogólności zagadnienia). Przyjmijmy zatem, że kolarz pokonuje 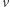 okrążeń toru w jednostce czasu. Po jej upływie wszyscy kolarze znajdą się ponownie razem w punkcie startu. Możemy więc przyjąć, że wyścig kończy się w tym momencie, gdyż nic nowego na torze już się nie wydarzy. Zgodnie ze wzorem na drogę w ruchu jednostajnym czas przejazdu kolarza przez łuk długości
okrążeń toru w jednostce czasu. Po jej upływie wszyscy kolarze znajdą się ponownie razem w punkcie startu. Możemy więc przyjąć, że wyścig kończy się w tym momencie, gdyż nic nowego na torze już się nie wydarzy. Zgodnie ze wzorem na drogę w ruchu jednostajnym czas przejazdu kolarza przez łuk długości 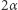 wynosi
wynosi 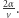 W ciągu całego wyścigu takich przejazdów jest dokładnie
W ciągu całego wyścigu takich przejazdów jest dokładnie 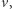 przy czym na jeden z nich składa się pierwszy i ostatni przejazd przez połowę świetlnego łuku. Stąd łączny czas przejazdu kolarza przez rejon światła to
przy czym na jeden z nich składa się pierwszy i ostatni przejazd przez połowę świetlnego łuku. Stąd łączny czas przejazdu kolarza przez rejon światła to 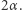 Wielkość ta jest niezależna od
Wielkość ta jest niezależna od 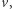 co nie jest chyba zaskakujące: szybszy kolarz szybciej mknie przez rejon światła, ale za to częściej weń wpada. Jeżeli przyjmiemy teraz, że
co nie jest chyba zaskakujące: szybszy kolarz szybciej mknie przez rejon światła, ale za to częściej weń wpada. Jeżeli przyjmiemy teraz, że 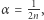 to widzimy, że całkowity czas, w którym przynajmniej jeden kolarz był w łuku świetlnym, wynosi co najwyżej
to widzimy, że całkowity czas, w którym przynajmniej jeden kolarz był w łuku świetlnym, wynosi co najwyżej 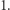 W rzeczywistości nie może być on równy
W rzeczywistości nie może być on równy 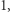 gdyż początkowo wszyscy kolarze są w pobliżu lampy. Musi zatem istnieć moment, w którym cały peleton zginie w gęstym mroku.
gdyż początkowo wszyscy kolarze są w pobliżu lampy. Musi zatem istnieć moment, w którym cały peleton zginie w gęstym mroku.
Wyobraźmy sobie teraz, że możemy regulować moc lampy, zwiększając stopniowo jej zasięg, począwszy od rozpiętości 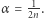 Zjawisko znikania peletonu w mroku będzie zapewne zachodzić przy delikatnym zwiększeniu mocy, ale pytanie jak długo? Hipoteza 2 mówi, że aż do
Zjawisko znikania peletonu w mroku będzie zapewne zachodzić przy delikatnym zwiększeniu mocy, ale pytanie jak długo? Hipoteza 2 mówi, że aż do 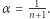 Tej ostatniej granicy nie da się już przekroczyć, co widać na przykładzie
Tej ostatniej granicy nie da się już przekroczyć, co widać na przykładzie 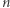 kolarzy jadących z prędkościami
kolarzy jadących z prędkościami 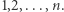 Jak dotąd, nikomu nie tylko nie udało się zbliżyć do hipotetycznej granicy, ale wręcz znacząco oddalić się od początkowej rozpiętości
Jak dotąd, nikomu nie tylko nie udało się zbliżyć do hipotetycznej granicy, ale wręcz znacząco oddalić się od początkowej rozpiętości 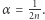 Nie wiadomo nawet tego, czy Hipoteza 2 zachodzi przy
Nie wiadomo nawet tego, czy Hipoteza 2 zachodzi przy 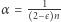 dla jakiegokolwiek
dla jakiegokolwiek 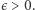 Najlepszy obecnie rezultat, należący do Terrenca Tao, potwierdza ją jedynie dla dostatecznie dużych
Najlepszy obecnie rezultat, należący do Terrenca Tao, potwierdza ją jedynie dla dostatecznie dużych  przy
przy 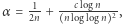 gdzie
gdzie  jest stałą dodatnią.
jest stałą dodatnią.
Inną prostą konsekwencją powyższych dywagacji jest taki oto dziwny fakt. Jak wykazaliśmy, całkowity czas pobytu każdego kolarza w rejonie światła wynosi 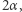 niezależnie od jego prędkości. Składa się on z rozłącznych odcinków czasowych. Jeżeli
niezależnie od jego prędkości. Składa się on z rozłącznych odcinków czasowych. Jeżeli 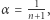 to suma długości wszystkich tych odcinków wynosi
to suma długości wszystkich tych odcinków wynosi 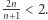 Co to znaczy? Pokolorujmy odcinki czasowe każdego kolarza innym kolorem, powiedzmy, kolorem jego koszulki. Mamy więc kolekcję odcinków w
Co to znaczy? Pokolorujmy odcinki czasowe każdego kolarza innym kolorem, powiedzmy, kolorem jego koszulki. Mamy więc kolekcję odcinków w  kolorach pokrywających jakoś jednostkowy przedział czasu. Całkowita suma ich długości jest mniejsza od
kolorach pokrywających jakoś jednostkowy przedział czasu. Całkowita suma ich długości jest mniejsza od 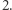 Musi zatem istnieć punkt pokryty co najwyżej jednym kolorem. Jest to punkt w czasie, w którym co najwyżej jeden kolarz znajduje się w rejonie światła. Udowodniliśmy w ten sposób następujące twierdzenie.
Musi zatem istnieć punkt pokryty co najwyżej jednym kolorem. Jest to punkt w czasie, w którym co najwyżej jeden kolarz znajduje się w rejonie światła. Udowodniliśmy w ten sposób następujące twierdzenie.

Twierdzenie 1. W każdym peletonie istnieje kolarz, którego dyskwalifikacja gwarantuje zniknięcie pozostałych kolarzy w mroku.
Niestety, nie wiemy, który to kolarz. Gdyby teza twierdzenia zachodziła dla dowolnie wybranego kolarza, oznaczałoby to, że Hipoteza 2 jest prawdziwa przy 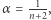 co w porównaniu ze wspomnianym rezultatem Tao byłoby zaiste rewelacją. Powyższe twierdzenie skłania do następującego osłabienia Hipotezy 1, o które zapytał Joel Spencer.
co w porównaniu ze wspomnianym rezultatem Tao byłoby zaiste rewelacją. Powyższe twierdzenie skłania do następującego osłabienia Hipotezy 1, o które zapytał Joel Spencer.
Jest rzeczą zadziwiającą, że mimo tak znacznego osłabienia tezy, wszak zamieniliśmy kwantyfikator ogólny na egzystencjalny, niczego istotnego nie udało się udowodnić.
Na koniec przedstawimy jednak pewien nieprawdopodobny wynik, który budzi nadzieję na ostateczne zwycięstwo. Rozważmy sytuację, w której prędkości kolarzy wybieramy losowo ze zbioru 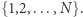 Niech
Niech 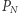 oznacza prawdopodobieństwo, że taki losowy peleton spełnia Hipotezę 2.
oznacza prawdopodobieństwo, że taki losowy peleton spełnia Hipotezę 2.
Jeżeli jest ona prawdziwa, to, oczywiście, 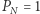 dla każdego
dla każdego 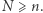 Powiemy, że Hipoteza 2 jest prawie na pewno prawdziwa, jeżeli
Powiemy, że Hipoteza 2 jest prawie na pewno prawdziwa, jeżeli 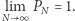 Poniższe twierdzenie, udowodnione przez Sebastiana Czerwińskiego, pokazuje, że dużo silniejsza wersja Hipotezy 2 jest prawie na pewno prawdziwa.
Poniższe twierdzenie, udowodnione przez Sebastiana Czerwińskiego, pokazuje, że dużo silniejsza wersja Hipotezy 2 jest prawie na pewno prawdziwa.
Twierdzenie 2. Losowy peleton prawie na pewno zniknie w ciemności, nawet jeżeli prawie cały tor jest oświetlony.
Mamy tu na myśli, że Hipoteza 2 jest prawie na pewno prawdziwa przy 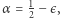 dla każdego
dla każdego 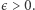 Twierdzenie to wzmocnił i uogólnił Noga Alon, upraszczając przy okazji dowód Czerwińskiego. Udowodnił on, że dowolnie wybrani kolarze losowego peletonu znajdą się w pewnej chwili dowolnie blisko dowolnie wybranych punktów toru.
Twierdzenie to wzmocnił i uogólnił Noga Alon, upraszczając przy okazji dowód Czerwińskiego. Udowodnił on, że dowolnie wybrani kolarze losowego peletonu znajdą się w pewnej chwili dowolnie blisko dowolnie wybranych punktów toru.