Perkolacje
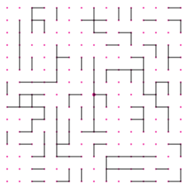
Rys. 1. Woda płynie wzdłuż czarnych linii.
Wyobraźmy sobie porowaty materiał, może to być gleba, a może to być... ubita kawa w kawiarce. Czy przez ten materiał można przesączyć wodę? Intuicyjnie wiemy, że jest to możliwe w przypadku kawy, ale już w przypadku gleby zależy od jej rodzaju, a dokładniej - od struktury "porów wolnej przestrzeni". W roku 1957 matematycy angielscy, Simon Broadbent i John Hammersley, zaproponowali probabilistyczny model opisujący materiały porowate. Pomimo prostoty definicji model ten (zwany perkolacjami) okazał się fascynującym tematem badań. Wspomnijmy, że, między innymi, za wyniki dotyczące perkolacji Stanisław Smirnow został nagrodzony w 2010 roku najwyższym matematycznym wyróżnieniem, Medalem Fieldsa.
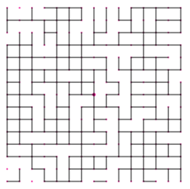
Rys. 2
Czym jest perkolacja? Wyobraźmy sobie stronę zeszytu w kratkę. Każda jej krawędź może być otwarta ( "przepuszczająca wodę") lub zamknięta ( "nieprzepuszczająca wody"). O otwarciu krawędzi decydujemy w sposób losowy, rzucając kostką sześcienną. Rozważmy dwa przypadki. W pierwszym z nich otwieramy krawędź, gdy na kostce wypadnie 1 lub 2. Rysunek 1 przedstawia przykładowy rezultat takiego losowego doświadczenia - jak widać, nie istnieje otwarta ścieżka z góry na dół, którą woda mogłaby przepłynąć. W drugim przypadku otwieramy krawędź, gdy na kostce wypadnie jedna z liczb 1, 2, 3, 4. Intuicyjnie łatwo stwierdzić, że szansa przepłynięcia wody gwałtownie rośnie, co ilustruje drugi rysunek. Wspomniani już Broadbent i Hammersley przekuli powyższe intuicje w abstrakcyjny model matematyczny. Rozważmy nieskończony graf regularny (może to być nieskończona kartka w kratkę, czyli graf 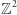 ). Każdą z jego krawędzi otwieramy niezależnie z pewnym prawdopodobieństwem
). Każdą z jego krawędzi otwieramy niezależnie z pewnym prawdopodobieństwem 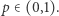 Kluczowe w teorii perkolacji jest pytanie "jakie jest prawdopodobieństwo, że krawędzie otwarte łączą się w nieskończony zbiór?". Intuicyjnie jest oczywiste, że szansa ta zwiększa się wraz ze wzrostem
Kluczowe w teorii perkolacji jest pytanie "jakie jest prawdopodobieństwo, że krawędzie otwarte łączą się w nieskończony zbiór?". Intuicyjnie jest oczywiste, że szansa ta zwiększa się wraz ze wzrostem 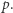 Sugeruje to istnienie takiego prawdopodobieństwa krytycznego
Sugeruje to istnienie takiego prawdopodobieństwa krytycznego 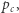 że dla
że dla 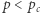 nie ma nieskończonego zbioru otwartego (woda nie może przepływać), a dla
nie ma nieskończonego zbioru otwartego (woda nie może przepływać), a dla 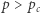 taki zbiór ma szansę powstać. Jednym z pierwszych osiągnięć teorii perkolacji było pokazanie, że prawdopodobieństwo krytyczne dla
taki zbiór ma szansę powstać. Jednym z pierwszych osiągnięć teorii perkolacji było pokazanie, że prawdopodobieństwo krytyczne dla 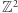 jest nietrywialne, mianowicie, że
jest nietrywialne, mianowicie, że 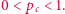
Pokażemy teraz szkic argumentu pokazującego, że dla 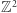 mamy
mamy 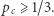 Rozważmy kwadrat na kartce papieru o boku
Rozważmy kwadrat na kartce papieru o boku 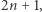 czyli zbiór
czyli zbiór 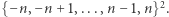 Zastanówmy się, czy środek tego kwadratu jest połączony za pomocą krawędzi otwartych z jakimś punktem brzegu. Jeśli tak, to istnieje ścieżka o długości
Zastanówmy się, czy środek tego kwadratu jest połączony za pomocą krawędzi otwartych z jakimś punktem brzegu. Jeśli tak, to istnieje ścieżka o długości 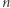 złożona z krawędzi otwartych, zaczynająca się w
złożona z krawędzi otwartych, zaczynająca się w 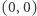 (np. będąca częścią ścieżki otwartej do brzegu). Zauważmy, że liczbę wszystkich ścieżek o długości
(np. będąca częścią ścieżki otwartej do brzegu). Zauważmy, że liczbę wszystkich ścieżek o długości  możemy oszacować przez
możemy oszacować przez 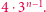 Szansa na to, że każda z krawędzi takiej ścieżki jest otwarta, wynosi
Szansa na to, że każda z krawędzi takiej ścieżki jest otwarta, wynosi 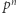 (korzystamy z założenia o niezależności). Jeden z podstawowych wyników teorii prawdopodobieństwa mówi, że szansa na otwarcie przynajmniej jednej ścieżki jest mniejsza niż suma prawdopodobieństw otwarcia poszczególnych ścieżek, co w naszym przypadku wynosi
(korzystamy z założenia o niezależności). Jeden z podstawowych wyników teorii prawdopodobieństwa mówi, że szansa na otwarcie przynajmniej jednej ścieżki jest mniejsza niż suma prawdopodobieństw otwarcia poszczególnych ścieżek, co w naszym przypadku wynosi 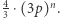 W ostatnim kroku obserwujemy, że liczba ta jest bardzo mała, gdy
W ostatnim kroku obserwujemy, że liczba ta jest bardzo mała, gdy 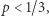 a
a  jest duże. W związku z tym łatwo uwierzyć (a także matematycznie wykazać), że każdy z połączonych zbiorów krawędzi otwartych będzie wtedy skończony. Nasze rozważania pokazują zatem, że
jest duże. W związku z tym łatwo uwierzyć (a także matematycznie wykazać), że każdy z połączonych zbiorów krawędzi otwartych będzie wtedy skończony. Nasze rozważania pokazują zatem, że 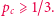
Podobny, choć trudniejszy, argument pokazuje, że dla 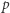 bliskich jedynki nieskończony zbiór otwarty zawierający
bliskich jedynki nieskończony zbiór otwarty zawierający 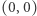 ma szansę powstać. Zachęcamy Czytelnika do próby uzasadnienia tego faktu. Kluczową obserwacją jest to, że jeśli zbiór jest skończony, to istnieje "pętla" otaczająca
ma szansę powstać. Zachęcamy Czytelnika do próby uzasadnienia tego faktu. Kluczową obserwacją jest to, że jeśli zbiór jest skończony, to istnieje "pętla" otaczająca 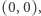 przecinająca jedynie zamknięte krawędzie.
przecinająca jedynie zamknięte krawędzie.

Przykład perkolacji na plastrze miodu. Woda płynie przez pola ciemne.
Główną trudnością w analizie perkolacji są nietrywialne zależności geometryczne. Jednocześnie są one źródłem wielu ciekawych fenomenów sprawiających, że perkolacje są interesującym modelem. W naszej analizie badaliśmy "oddzielnie" ścieżki długości 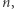 tymczasem wiele z nich się pokrywa. Mimo że przedstawione argumenty można poprawić, uzyskanie wartości
tymczasem wiele z nich się pokrywa. Mimo że przedstawione argumenty można poprawić, uzyskanie wartości 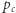 wymagało znacznie bardziej zaawansowanych metod, których opracowanie trwało 20 lat i zostało uwieńczone dowodem Harrego Kestena pokazującym, że
wymagało znacznie bardziej zaawansowanych metod, których opracowanie trwało 20 lat i zostało uwieńczone dowodem Harrego Kestena pokazującym, że 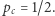
Uzyskanie dokładnych wartości prawdopodobieństwa krytycznego dla innych grafów często jest niemożliwe. Zaskakująco nie przeszkadza to w badaniu zachowania perkolacji w punkcie krytycznym. Jest to najbardziej aktywne pole rozwoju teorii (te zagadnienia były badane przez Smirnowa). Mimo że wykazano to ściśle w małej ilości przypadków, spodziewamy się, że zachowanie w dużej skali w tym punkcie zależy głównie od wymiaru grafu (na przykład zachowanie perkolacji na "kartce w kratkę" będzie podobne jak na "plastrze miodu"). Fenomen ten, zwany uniwersalnością, jest przedmiotem intensywnych badań, poprzez swoje związki z innymi dziedzinami matematyki. Zapewne w najbliższych latach doprowadzi do nowych fascynujących wyników.
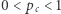 dla dowolnej kraty
dla dowolnej kraty 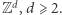 Dla małych
Dla małych 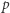 zbiory krawędzi otwartych są skończone, a dla
zbiory krawędzi otwartych są skończone, a dla 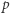 bliskich 1 istnieje (jeden) zbiór nieskończony.
bliskich 1 istnieje (jeden) zbiór nieskończony.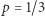 to rozumowanie daje trywialne szacowanie 4/3 na szansę połączenia środka z brzegiem. Symulacja komputerowa pokazuje, że dla
to rozumowanie daje trywialne szacowanie 4/3 na szansę połączenia środka z brzegiem. Symulacja komputerowa pokazuje, że dla 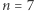 szansa ta wynosi około 8% (przykładowy rezultat takiej symulacji pokazany jest na pierwszym rysunku).
szansa ta wynosi około 8% (przykładowy rezultat takiej symulacji pokazany jest na pierwszym rysunku).