Mathematica i fraktale

Wolfram Mathematica to popularny, nie tylko wśród studentów matematyki, system obliczeniowy, który umożliwia rozwiązywanie zadań z dziedzin, takich jak matematyka, fizyka czy ekonomia. Mamy tu oczywiście rachunek różniczkowy i całkowy, algebrę i statystykę, lecz także najróżniejsze metody z zakresu od matematyki czysto teoretycznej aż po zastosowania w data science, biznesie, inżynierii czy medycynie. Łącznie mamy prawie 5000 wzajemnie zintegrowanych, wbudowanych funkcji. Mathematica używa własnego języka programowania Wolfram Language, który cechuje się wydajnym operowaniem na listach. Zaletą systemu Mathematica jest także przyjazny interfejs z rozbudowaną dokumentacją każdej z funkcji, a także szerokie możliwości interaktywnej wizualizacji obliczeń.
Choć zastosowania Mathematici są bardzo szerokie, tutaj skupię się na tych czysto teoretycznych. Pokażę bowiem, jak Mathematicę zastosować do elementarnej teorii fraktali. Opiszę założenia teoretyczne oraz pokażę funkcje, dzięki którym użytkownik może sprawdzać poprawność danych wejściowych, obliczać analitycznie i numerycznie wymiar Hausdorffa i wreszcie generować piękne wizualizacje fraktali!

Rys. 1 Wizualizacja kolejnych iteracji fraktala, stworzona w Mathematice
Fraktale na kartce
Zanim zaczniemy programować, przybliżmy nieco temat fraktali. Różne są definicje fraktali. Mówiąc o fraktalach, mamy zwykle na myśli zbiory w przestrzeni 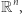 które są samopodobne, a więc składają się z wielu przeskalowanych kopii samych siebie.
które są samopodobne, a więc składają się z wielu przeskalowanych kopii samych siebie.
Matematyk zwykle powie, że fraktal to zbiór, którego wymiar Hausdorffa jest większy od jego wymiaru topologicznego. O wymiarze Hausdorffa można myśleć jako o uogólnieniu wymiaru topologicznego dla zbiorów, których nie da się łatwo sparametryzować. O fraktalach możemy myśleć jako o zbiorach (zwykle) niecałkowitego wymiaru!
Formalnie, dla zbioru 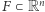 i
i 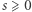 definiujemy
definiujemy  -wymiarową miarę Hausdorffa:
-wymiarową miarę Hausdorffa:

gdzie 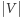 oznacza średnicę zbioru
oznacza średnicę zbioru 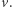 Mówiąc prościej, ustalamy
Mówiąc prościej, ustalamy 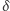 i
i  i pokrywamy zbiór
i pokrywamy zbiór 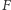 zbiorami o średnicy nie większej niż
zbiorami o średnicy nie większej niż 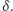 Ze wszystkich takich pokryć wybieramy to, które minimalizuje wyrażenie
Ze wszystkich takich pokryć wybieramy to, które minimalizuje wyrażenie 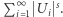 Następnie zmniejszamy
Następnie zmniejszamy  Klasa możliwych pokryć zbioru będzie się zmniejszać, zatem infimum będzie rosnąć. Okazuje się, że zbiegając z
Klasa możliwych pokryć zbioru będzie się zmniejszać, zatem infimum będzie rosnąć. Okazuje się, że zbiegając z  do zera, otrzymamy konkretną granicę
do zera, otrzymamy konkretną granicę 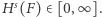 O mierze tej wiemy, że przyjmuje stale wartość
O mierze tej wiemy, że przyjmuje stale wartość  aż do pewnego
aż do pewnego 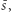 powyżej którego jest stale równa 0. Właśnie to
powyżej którego jest stale równa 0. Właśnie to 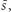 dla którego następuje swoista "nieciągłość" miary, to nasz wymiar Hausdorffa:
dla którego następuje swoista "nieciągłość" miary, to nasz wymiar Hausdorffa:

Wyznaczanie wymiaru Hausdorffa z tej definicji jest zwykle bardzo trudne. W naszym programie rozpatrywać będziemy jednak tylko szczególną klasę fraktali, dla których szczęśliwie zachodzi pewne dogodne twierdzenie.
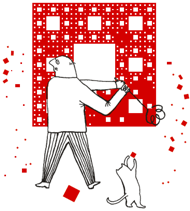
Fraktale powstawać będą rekurencyjnie wewnątrz kwadratu podzielonego na równą siatkę. W pierwszym kroku wczytywana jest lista współrzędnych i wielkości kwadratów, które zaznaczane są na siatce. Kwadraty mogą mieć wspólną co najwyżej krawędź lub wierzchołek i nie mogą wystawać poza linie siatki. Cały obraz jest następnie skalowany i rysowany w każdym z zaznaczonych kwadratów. Procedurę tę powtarza się kilka razy, aż do określonej liczby rekurencji. Mamy więc funkcje podobieństw 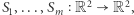 które przekształcają cały zbiór na jeden z mniejszych kwadratów, ze skalami podobieństw
które przekształcają cały zbiór na jeden z mniejszych kwadratów, ze skalami podobieństw 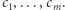 Formalnie nasz fraktal jest tzw. atraktorem układu iterowanych odwzorowań. Zachodzi wówczas następujące twierdzenie:
Formalnie nasz fraktal jest tzw. atraktorem układu iterowanych odwzorowań. Zachodzi wówczas następujące twierdzenie:
Twierdzenie. Załóżmy, że podobieństwa 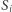 ze skalami
ze skalami 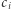 (dla
(dla 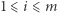 ) spełniają warunek otwartego zbioru. Wówczas, jeśli
) spełniają warunek otwartego zbioru. Wówczas, jeśli 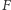 jest zbiorem niezmienniczym ze względu na
jest zbiorem niezmienniczym ze względu na 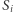 (tzn. spełniającym
(tzn. spełniającym 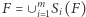 ), to wymiar Hausdorffa
), to wymiar Hausdorffa 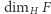 jest skończony i zadany rozwiązaniem równania
jest skończony i zadany rozwiązaniem równania 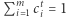 ze względu na parametr
ze względu na parametr 
Fraktale w Mathematice
Mając już zaplecze teoretyczne, przejdźmy do Mathematici. Na rysunku 2 widzimy trzy przykładowe okna końcowego wyniku programu, który napisałem w Mathematice.

Rys. 2 Interaktywne okna programu
Mamy tutaj okno z interaktywnym interfejsem oraz parametrami (po lewej) i wizualizacją (po prawej). Z rozwijanej listy preset możemy wybrać domyślny zbiór początkowy, taki jak sierpinski triangle, lub wybrać custom i wpisać własny. Robimy to, ustalając parametr division (rozdzielczość kwadratu) i wpisując współrzędne i wielkości kwadratów w listę w obszarze initial set. Kolejne iteracje zbioru możemy potem generować, zwiększając parametr iteration. Za pomocą przycisku grid możemy wyświetlić siatkę, a za pomocą zoomed square i zoom value uruchomić animację przybliżania wybranego fragmentu fraktala. Poniżej znajduje się przycisk inverse do inwersji kolorów i suwaki kolorów: fractal i background. Dalej mamy pokazane parametry fraktala: długość danych wejściowych input length i limit iteracji iterations (obliczany za pomocą prostej funkcji ze względów wydajnościowych). Wreszcie, na samym dole mamy wyświetlony wymiar Hausdorffa: dokładny - exact (o ile analityczne wyznaczenie jest możliwe) oraz przybliżony - approx.
Widać, że oprócz obszaru wyświetlania mamy tu kontrole najróżniejszych typów: listy rozwijane, pola wyboru, pola tekstowe, suwaki i palety kolorów. W Mathematice taki interfejs można łatwo stworzyć za pomocą funkcji Manipulate, która opisuje dynamiczne środowisko do obliczeń. Pierwszym argumentem funkcji jest wyrażenie, które ma być dynamicznie aktualizowane. W naszym przypadku są to wszystkie niezbędne obliczenia i rekurencyjna formuła generująca grafikę. Drugim argumentem jest lista kontrolowalnych parametrów i ich ustawienia. Oprócz tego możemy też podać opcje, które pomogą nam dostosować zachowanie i wygląd środowiska. Wszystkie te trzy elementy występują na schemacie 1.

Schemat 1 Fragment głównej funkcji programu.
Omówimy teraz funkcję obliczającą współrzędne kwadratów do wyświetlenia przedstawioną na schemacie 2. Funkcja ta podzielona jest na cztery mniejsze funkcje. Pierwsza z nich, nazwana shift, bierze listę kwadratów i numer jednego z nich. Za pomocą obliczeń algebraicznych zwraca listę kwadratów o współrzędnych zaczepionych w danym kwadracie. Następna funkcja to scor, która zwraca współrzędne wszystkich kwadratów w następnej iteracji, a więc zwraca długą listę kwadratów potraktowanych funkcją shift. Korzystamy tutaj ze wbudowanej instrukcji Table tworzącej listę oraz wbudowanej funkcji Flatten, która listę list spłaszcza do jednej długiej listy. Ostatnia z naszych funkcji to fscor, która zagnieżdża funkcję scor aż do limitu iteracji. Zagnieżdżanie funkcji robimy za pomocą wbudowanej funkcji Nest. Otrzymujemy więc bardzo długą listę współrzędnych małych kwadratów. Na koniec zamieniamy ją na obiekty graficzne typu Rectangle za pomocą funkcji square. Ostatecznie przykładamy funkcję square do wszystkich elementów listy, za pomocą operatora /@. Na wyjściu mamy więc listę kwadratów, które wyświetlamy potem w głównej funkcji wewnątrz środowiska Graphics.

Schemat 2 Funkcja licząca współrzędne kwadratów.
Mamy już wizualizację, omówmy zatem funkcje obliczające wymiar Hausdorffa przedstawione na schemacie 3. Są to funkcje dimension oraz ndimension, które obliczają odpowiednio dokładny i przybliżony wymiar. Pierwsza z nich korzysta ze wbudowanej funkcji Solve, która w analityczny sposób próbuje rozwiązać układ równań. Funkcja ta nie zawsze prowadzi do rozwiązania. W takim przypadku za pomocą instrukcji If powodujemy, aby zwróciła odpowiedni napis. Druga funkcja używa bardzo podobnej wbudowanej funkcji NSolve. Różnica jest taka, że wynik wyznaczony jest numerycznie z odpowiednią precyzją. Zawsze otrzymamy wynik jako przybliżoną liczbę wymierną w zapisie dziesiętnym. W Mathematice występuje wiele funkcji z dodaną w nazwie literą N. W szczególności sama funkcja N zwraca zaokrągloną wartość w systemie dziesiętnym. Takie funkcje są szczególnie przydatne, gdy nie mamy pewności, że rozwiązanie analityczne nie istnieje, tak jak w naszym przypadku.
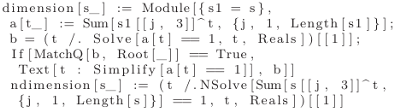
Schemat 3 Funkcje liczące wymiar Hausdorffa.
W programie mamy także kilka funkcji sprawdzających poprawność danych wprowadzonych przez użytkownika (aby zapobiec nieprzewidzianym zachowaniom programu). Jedną z nich jest funkcja checkPattern, która sprawdza, czy wejście spełnia podstawowe założenia, tzn. jest listą trójek złożonych z liczb całkowitych. W funkcji tej wykorzystywane są tzw. wzorce, czyli zapytania dotyczące liczby i rodzaju argumentów. Przykładowo wzorzec List[__] oznacza listę z dowolną liczbą argumentów, a List[_Integer, _Integer, _Integer] oznacza listę złożoną z trzech liczb całkowitych. Wzorce są sprawdzane za pomocą wbudowanej funkcji MatchQ. U nas sprawdzamy najpierw, czy na wejściu otrzymaliśmy listę (jeśli nie, to zwracamy domyślny zbiór). Następnie, za pomocą pętli For, przechodzimy po całej liście, sprawdzając, czy są to trójki liczb całkowitych. Elementy niepasujące do tego wzorca są usuwane za pomocą wbudowanej funkcji Delete.

Schemat 4 Jedna z funkcji sprawdzająca poprawność danych wejściowych.
Program składa się jeszcze z kilku elementów, których nie pokazaliśmy. Przedstawione tu funkcje pokazują jednak główną ideę działania programu w Mathematice. Wykorzystaliśmy wbudowane funkcjonalności Mathematici, takie jak środowisko Dynamic (funkcja Manipulate), funkcje operujące na listach (Flatten, Table, operatory), zagnieżdżanie funkcji (funkcja Nest), analityczne i numeryczne obliczanie równań (funkcje Solve i NSolve) oraz różne funkcje operujące na wzorcach. Użyliśmy także konstrukcji typowych dla języków programowania, takich jak If czy For. Za pomocą kilku średniej długości funkcji stworzyliśmy rozbudowane narzędzie do wizualizacji fraktali i obliczenia wymiaru Hausdorffa, co jest przecież zadaniem dość nietrywialnym.
 nie pokrywają się zanadto. Dokładnie mówi on, że istnieje taki niepusty ograniczony zbiór otwarty
nie pokrywają się zanadto. Dokładnie mówi on, że istnieje taki niepusty ograniczony zbiór otwarty 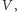 że
że 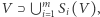 przy czym suma ta jest rozłączna. U nas jako
przy czym suma ta jest rozłączna. U nas jako 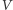 wystarczy wziąć wnętrze dużego kwadratu. Obrazy podobieństw zbioru początkowego leżą wówczas we wnętrzach małych kwadratów, które są rozłączne i zawierają się we wnętrzu dużego kwadratu.
wystarczy wziąć wnętrze dużego kwadratu. Obrazy podobieństw zbioru początkowego leżą wówczas we wnętrzach małych kwadratów, które są rozłączne i zawierają się we wnętrzu dużego kwadratu.