Równanie z dreszczykiem
Jakiś czas temu Marek Bodnar z sąsiedniego Zakładu Biomatematyki pokazał mi niepozornie wyglądające równanie różniczkowe, które pojawiło się w pewnym modelu przebiegu choroby zakaźnej...
Oto ono
 |
(1) |
Liczby 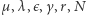 są stałymi, dodatnimi parametrami modelu (zob.
są stałymi, dodatnimi parametrami modelu (zob. ![|[1,2]](/math/temat/matematyka/zastosowania/2018/04/24/Rownanie_z_dreszczykiem/3x-027fdb17e0843de5316dacd8f36df04e4a1f7863-im-33,33,33-FF,FF,FF.gif) ). Niewiadomą jest funkcja
). Niewiadomą jest funkcja 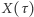 odpowiadająca liczbie chorych przypadających na jednostkę powierzchni. Zmienna niezależna
odpowiadająca liczbie chorych przypadających na jednostkę powierzchni. Zmienna niezależna 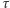 to czas. Odpowiednio skalując zmienne występujące w równaniu, możemy sprowadzić je do prostszej, równoważnej postaci
to czas. Odpowiednio skalując zmienne występujące w równaniu, możemy sprowadzić je do prostszej, równoważnej postaci
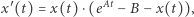 |
(2) |
przy czym 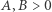 zależą od parametrów oryginalnego zadania. Dodatkowo na rozwiązanie nakładamy warunek
zależą od parametrów oryginalnego zadania. Dodatkowo na rozwiązanie nakładamy warunek 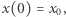 gdzie
gdzie 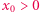 jest kolejnym parametrem zadania.
jest kolejnym parametrem zadania.
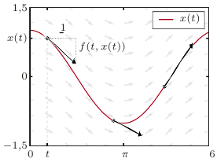
Rys. 1 Wykres rozwiązania 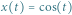 równania
równania  w każdym swoim punkcie
w każdym swoim punkcie  jest styczny do wektora
jest styczny do wektora 
Jest to równanie różniczkowe Bernoulliego drugiego stopnia. Czytelnikom nie w pełni zaznajomionym z teorią równań różniczkowych wyjaśnijmy, że wykres poszukiwanej przez nas funkcji 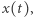 spełniającej równanie różniczkowe zapisane w ogólnej postaci
spełniającej równanie różniczkowe zapisane w ogólnej postaci
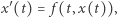 |
(3) |
ma taką własność, że jest on styczny w każdym swoim punkcie 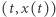 do wektora o kierunku
do wektora o kierunku ![|[1, f (t,x(t))],](/math/temat/matematyka/zastosowania/2018/04/24/Rownanie_z_dreszczykiem/4x-9157b4b2277220612d635fb313cd7ed76bdee326-im-33,33,33-FF,FF,FF.gif) zob. przykład na rysunku 1 dla
zob. przykład na rysunku 1 dla 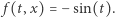 W przypadku równania (2), oczywiście,
W przypadku równania (2), oczywiście,  jest inne, równe
jest inne, równe 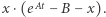
Równanie różniczkowe? Ależ to proste!
W dzisiejszych czasach zdawać by się mogło, że nie musimy rozumieć, czym jest równanie różniczkowe - wystarczy tylko wiedzieć, z jakiej biblioteki numerycznej skorzystać na swoim laptopie… Rzeczywiście: jedna z najlepszych (LSODE) jest wbudowana w darmowy pakiet obliczeń komputerowych GNU Octave; inne, równie znakomite, są używane przez MATLAB-a, Scipy, Mathematicę, itd. Dlatego codziennie naukowcy i inżynierowie z całego świata wykorzystują je do rutynowego numerycznego rozwiązywania równań różniczkowych na komputerze, ufając ich technicznej doskonałości i wbudowanej wiedzy, obejmującej kilkanaście (lub więcej) lat użytkowania w najróżniejszych warunkach.

Rys. 2 Metoda Eulera, wymyślona przez króla matematyków podobno na potrzeby przybliżonego rozwiązania zadania z hydrauliki fontann dla króla Prus. Tutaj zastosowana do zadania z rysunku 1, dla 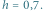
Jak działa taka biblioteka? Najprostszą strategią numerycznej aproksymacji rozwiązania równania (3) jest przyjęcie, że na krótkich odcinkach czasu długości 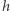 funkcja
funkcja 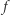 jest stała (innymi słowy, że rozwiązanie jest funkcją liniową), co prowadzi do tzw. metody Eulera:
jest stała (innymi słowy, że rozwiązanie jest funkcją liniową), co prowadzi do tzw. metody Eulera:

gdzie 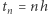 oraz (można udowodnić, że)
oraz (można udowodnić, że) 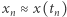 (zob. rys. 2). Nietrudno zgadnąć, że oprócz tej prościutkiej metody są też bardziej zaawansowane, np. schematy wielokrokowe lub metody Rungego-Kutty - również w wersjach, które dodatkowo automatycznie dopasowują długość
(zob. rys. 2). Nietrudno zgadnąć, że oprócz tej prościutkiej metody są też bardziej zaawansowane, np. schematy wielokrokowe lub metody Rungego-Kutty - również w wersjach, które dodatkowo automatycznie dopasowują długość  do rzeczywistego przebiegu rozwiązania tak, by zagwarantować spełnienie określonych przez użytkownika kryteriów tolerancji. Wspomniany powyżej LSODE używa właśnie schematów wielokrokowych z adaptacją długości kroku.
do rzeczywistego przebiegu rozwiązania tak, by zagwarantować spełnienie określonych przez użytkownika kryteriów tolerancji. Wspomniany powyżej LSODE używa właśnie schematów wielokrokowych z adaptacją długości kroku.
Febra wykresu: rozpoznanie, diagnoza i kuracja

Rys. 3 U góry: rozwiązania dla różnych wartości parametru 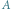 modelu (2) tylko z pozoru wyglądają sensownie. Na dole: rozwiązania wyznaczone dla tej samej wartości
modelu (2) tylko z pozoru wyglądają sensownie. Na dole: rozwiązania wyznaczone dla tej samej wartości  ale przy różnych tolerancjach (atol, rtol) pracy LSODE znacznie się różnią (jedno wygląda wręcz na zerowe), co jest bardzo podejrzane.
ale przy różnych tolerancjach (atol, rtol) pracy LSODE znacznie się różnią (jedno wygląda wręcz na zerowe), co jest bardzo podejrzane.
Używając wbudowanej w pakiet Octave biblioteki LSODE do rozwiązania (2) dla parametrów  i kilku wybranych wartości
i kilku wybranych wartości 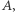 odpowiednich dla modelowanego zjawiska, dostaniemy ładne wykresy, takie jak na rysunku 3 na górze.
odpowiednich dla modelowanego zjawiska, dostaniemy ładne wykresy, takie jak na rysunku 3 na górze.
Jak zauważył Marek Bodnar (i dlatego pokazał mi to równanie, bo wie, że lubię takie smaczki), gdy ustalimy zestaw parametrów zadania, ale za to będziemy bawić się tolerancjami pracy LSODE, otrzymamy podobne, lecz jednak zdecydowanie różne rozwiązania (rys. 3 na dole). (Zobacz też uwagi J. Banasiaka w [2, str. 36]. Analogiczne zjawisko pojawi się także w MATLAB-ie i in.)
Jak to rozsądzić? Kto przeszedł kurs Równań różniczkowych zwyczajnych, ten zauważy, że (2) tylko troszkę różni się od klasycznego równania logistycznego

dla którego znamy jawny wzór na rozwiązanie:

Gdyby więc - podobnie jak w metodzie Eulera - przyjąć chwilowo, że człon 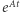 jest stałą wynoszącą, powiedzmy,
jest stałą wynoszącą, powiedzmy,  to wtedy (2) zamienia się w równanie logistyczne z
to wtedy (2) zamienia się w równanie logistyczne z 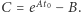
Ta wiedza pozwoli nam rozstrzygnąć, które z uzyskanych przez nas rozwiązań jest akceptowalne. Wykorzystamy następujące twierdzenie porównawcze:
Twierdzenie (Peano). Jeśli funkcje ![x,y [0,T] R](/math/temat/matematyka/zastosowania/2018/04/24/Rownanie_z_dreszczykiem/1x-21de1fc977efe441217697dc99d71c4f7568e838-im-33,33,33-FF,FF,FF.gif) są różniczkowalne i spełniają dla
są różniczkowalne i spełniają dla 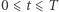 warunki:
warunki:

to  dla
dla 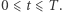
Z tego, co powiedzieliśmy wcześniej, wynika, że jako 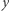 wystarczy wziąć rozwiązanie równania logistycznego z
wystarczy wziąć rozwiązanie równania logistycznego z 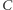 ciut mniejszym niż
ciut mniejszym niż 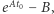 gdyż w naszym zadaniu
gdyż w naszym zadaniu 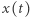 jest zawsze dodatnie. Łatwo też uzupełnić treść powyższego twierdzenia tak, aby otrzymać analogiczne dolne oszacowanie
jest zawsze dodatnie. Łatwo też uzupełnić treść powyższego twierdzenia tak, aby otrzymać analogiczne dolne oszacowanie 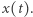 Ponadto nic nie stoi na przeszkodzie, byśmy zastosowali je - podobnie jak w metodzie Eulera - nie od razu dla wszystkich
Ponadto nic nie stoi na przeszkodzie, byśmy zastosowali je - podobnie jak w metodzie Eulera - nie od razu dla wszystkich 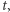 ale wielokrotnie na krótkich odcinkach długości, powiedzmy,
ale wielokrotnie na krótkich odcinkach długości, powiedzmy,  W ten sposób dostajemy dwie - jak się okazuje, całkiem bliskie - krzywe, będące ścisłymi oszacowaniami z góry i z dołu dla prawdziwego (wciąż nieznanego!) rozwiązania (2): obie zostały naszkicowane na rysunku 4.
W ten sposób dostajemy dwie - jak się okazuje, całkiem bliskie - krzywe, będące ścisłymi oszacowaniami z góry i z dołu dla prawdziwego (wciąż nieznanego!) rozwiązania (2): obie zostały naszkicowane na rysunku 4.
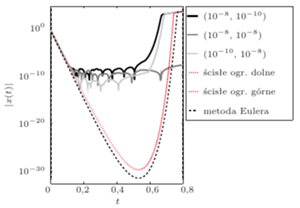
Rys. 4 Wykresy rozwiązań LSODE w skali logarytmicznej ukazują podejrzane zachowanie dla małych wartości 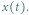 Górne i dolne oszacowanie na bazie twierdzenia Peano są tak bliskie, że na rysunku wyglądają jak jedna krzywa.
Górne i dolne oszacowanie na bazie twierdzenia Peano są tak bliskie, że na rysunku wyglądają jak jedna krzywa.
Podobnemu wykresowi, z MATLAB-a, przyglądaliśmy się w poprzednim numerze Delty.
Mt 20,16 Niestety, na rysunku 4 widzimy także, iż żaden wcześniej otrzymany wykres LSODE nie mieści się w wyznaczonym przez nas korytarzu, w którym musi przebiegać rozwiązanie. I, niczym w biblijnej przypowieści, prymitywna metoda Eulera ostatecznie wygrywa z wyrafinowanym LSODE: rozwiązania wyznaczone przez jedną z najlepszych numerycznych bibliotek okazują się bowiem dramatycznie kiepskie tam, gdzie wartości są bardzo małe: wykres trzęsie się jak w febrze, choć z teorii wiadomo, że powinien być gładki.
Patrząc na rysunek 4, zaczynamy rozumieć, o co chodzi. Schemat taki, jak LSODE ma wbudowany mechanizm sterowania długością kroku (w zamyśle służący polepszeniu jakości rozwiązania!), który jednak najwyraźniej gubi się, gdy rozwiązanie staje się w specyficzny sposób czułe na niewielkie odchylenia od dokładnej wartości, a tak dzieje się, gdy rozwiązanie przybliża się do zera.
LSODE (w końcu) też daje radę! W takiej sytuacji - gdy zadanie staje się zbyt trudne dla używanej metody - numeryk często proponuje: Może więc zmieńmy… zadanie?! Faktycznie, wprowadzając w (2) nową niewiadomą  dostaniemy kolejne równoważne równanie:
dostaniemy kolejne równoważne równanie:
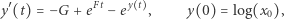 |
(4) |
gdzie parametry 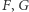 zależą od
zależą od  i
i  Rozwiązania tego równania mają znacznie spokojniejszy przebieg niż (2). LSODE rozwiązuje je bez trudu, więc kładąc następnie
Rozwiązania tego równania mają znacznie spokojniejszy przebieg niż (2). LSODE rozwiązuje je bez trudu, więc kładąc następnie  wyznaczamy znakomity wykres, nareszcie idealnie wpasowujący się pomiędzy górne i dolne ograniczenie. Nie pokazujemy tego wykresu, bo i tak w używanej przez nas skali będzie nieodróżnialny od krzywych ograniczających z rysunku 4.
wyznaczamy znakomity wykres, nareszcie idealnie wpasowujący się pomiędzy górne i dolne ograniczenie. Nie pokazujemy tego wykresu, bo i tak w używanej przez nas skali będzie nieodróżnialny od krzywych ograniczających z rysunku 4.
Walka nie jest jeszcze wygrana
Ale w życiu takie rzeczy nie zdarzają się, prawda? - chciałoby się zapytać, mając w pamięci, że cała technologiczna nowoczesność wokół nas była zapewne wcześniej testowana w modelach komputerowych, które - jak przekonuje nas codzienne doświadczenie - najwyraźniej musiały dać się numerycznie rozwiązać w wystarczająco dokładny sposób. Generalnie, metody numeryczne rzeczywiście działają zdumiewająco dobrze; jednak trafiają się spektakularne niepowodzenia - takie, jak zatonięcie 26 lat temu pływającej platformy wiertniczej Sleipner (zakończone wstrząsem tektonicznym o mocy 3 stopni w skali Richtera i stratą rzędu 700 mln dolarów) - spowodowane tylko jednym czynnikiem: zlekceważeniem naturalnych ograniczeń standardowych pakietów obliczeniowych.
Warto o tym pamiętać, naciskając klawisz Enter... i nie tylko.
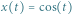 równania
równania 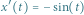 w każdym swoim punkcie
w każdym swoim punkcie  jest styczny do wektora
jest styczny do wektora 
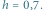
 modelu
modelu 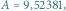 ale przy różnych tolerancjach (atol, rtol) pracy LSODE znacznie się różnią (jedno wygląda wręcz na zerowe), co jest bardzo podejrzane.
ale przy różnych tolerancjach (atol, rtol) pracy LSODE znacznie się różnią (jedno wygląda wręcz na zerowe), co jest bardzo podejrzane.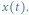 Górne i dolne oszacowanie na bazie twierdzenia Peano są tak bliskie, że na rysunku wyglądają jak jedna krzywa.
Górne i dolne oszacowanie na bazie twierdzenia Peano są tak bliskie, że na rysunku wyglądają jak jedna krzywa. odpowiada liczbie zarażonych w chwili
odpowiada liczbie zarażonych w chwili 