Wyznaczamy środek Polski
Według niezliczonych źródeł internetowych (w tym polskiej Wikipedii) geometryczny środek Polski znajduje się w miejscowości Piątek. Zastosowana do uzyskania tego wyniku metoda opiera się na wyznaczeniu figury sferycznej złożonej z fragmentów południków i równoleżników przechodzących przez najbardziej wysunięte w czterech kierunkach świata punkty naszego kraju, a następnie wyznaczeniu przecięcia ortodrom (są to "linie proste" na sferze, czyli fragmenty okręgów wielkich) łączących przekątniowo te cztery punkty.

Rys. 1 Środek Polski wyznaczony popularną metodą.
Warto zauważyć, że choć w przypadku Polski wynik (Rys. 1) nie budzi wyraźnych wątpliwości (choć konia z rzędem temu, komu w wyniku precyzyjnego zastosowania tej metody uda się otrzymać miejscowość Piątek), to wykorzystanie tej samej metody do dużo bardziej niesymetrycznego obszaru Stanów Zjednoczonych wraz z Alaską da w wyniku środek USA położony... w Kanadzie! Wpływ odległej Alaski okazuje się tutaj decydujący, pomimo że jej powierzchnia stanowi jedynie 18% powierzchni całego kraju. Ten sam problem, tylko z większym natężeniem, napotykamy w przypadku Rosji - dla tego kraju wyznaczony środek leży niemal na północnym biegunie geograficznym (Rys. 2).


Rys. 2 Środki Stanów Zjednoczonych i Rosji wyznaczone popularną metodą.
Czy można lepiej?
Podstawowy problem z powyższą metodą polega na zależności wyniku od wyboru układu współrzędnych. Przykładowo, gdybyśmy wykreślili mapę nie względem bieguna geograficznego, lecz np. magnetycznego, położenia południków i równoleżników zmieniłyby się. Inne byłyby zatem punkty skrajne we wszystkich kierunkach i w zupełnie innym punkcie otrzymalibyśmy przecięcie ortodrom, pomimo że zastosowaliśmy jedynie inny układ współrzędnych. Intuicyjnie zdajemy sobie natomiast sprawę, że w przypadku każdego rzeczywistego przedmiotu względne położenie jego "środka" (jakkolwiek zdefiniowanego) nie powinno zależeć od jego obrotu lub przesunięcia. Oczekiwalibyśmy więc tej samej prawidłowości również dla metody wyznaczania środka rozległego obszaru na kuli ziemskiej.
Analogia do rzeczywistych, trójwymiarowych obiektów kieruje naszą uwagę na pojęcie "środka masy" (środka ciężkości), które jest dobrze zdefiniowane dla obiektów o dowolnym kształcie i strukturze. W przypadku obiektów o stałej gęstości możemy mówić o pojęciu centroidu, zdefiniowanego jako średnia z położenia wszystkich punktów wchodzących w skład bryły lub figury geometrycznej. Warto zauważyć, że wyznaczony w ten sposób "środek" jest niezależny od wyboru układu współrzędnych.

Musimy, oczywiście, przyjąć pewne założenia: jako obszar Polski rozumiemy wielokąt sferyczny lub elipsoidalny o ustalonych wierzchołkach. Położenia tych wierzchołków możemy pobrać ze strony internetowej Centralnego Ośrodka Dokumentacji Geodezyjnej i Kartograficznej (www.codgik.gov.pl). Będziemy przy tym opierać nasze obliczenia o tzw. obszar administracyjny Polski, zawierający, poza obszarem lądowym, również polską część Zalewu Szczecińskiego, ale niezawierający polskiej części Zalewu Gdańskiego i Wiślanego.
Metoda
W przypadku figury płaskiej 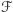 o
o 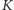 wierzchołkach
wierzchołkach 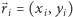 i polu powierzchni równym
i polu powierzchni równym  położenie środka masy
położenie środka masy 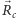 możemy obliczyć przy użyciu wzoru
możemy obliczyć przy użyciu wzoru
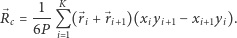 |
(1) |
Powyższa równość zachodzi wyłącznie dla figur płaskich, więc aby była dla nas użyteczna, musimy najpierw skorzystać z rzutowania (odwzorowania kartograficznego). Oznaczmy jako  obszar administracyjny Polski wyrażony we współrzędnych wybranego odwzorowania. Wykorzystując wprost powyższy wzór do całej figury
obszar administracyjny Polski wyrażony we współrzędnych wybranego odwzorowania. Wykorzystując wprost powyższy wzór do całej figury  wprowadzilibyśmy znaczący błąd związany z wyborem konkretnego odwzorowania oraz utracilibyśmy możliwość wykonywania dokładnych obliczeń w trzech wymiarach. Aby zminimalizować wpływ tego kroku, możemy podzielić figurę
wprowadzilibyśmy znaczący błąd związany z wyborem konkretnego odwzorowania oraz utracilibyśmy możliwość wykonywania dokładnych obliczeń w trzech wymiarach. Aby zminimalizować wpływ tego kroku, możemy podzielić figurę 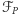 na
na 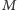 rozłącznych "komórek"
rozłącznych "komórek" 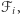 takich że
takich że 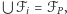 i skorzystać z następującej tożsamości dla środka masy:
i skorzystać z następującej tożsamości dla środka masy:
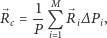 |
(2) |
gdzie 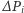 jest polem powierzchni komórki
jest polem powierzchni komórki 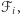 a
a 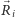 jest trójwymiarowym wektorem położenia jej środka masy.
jest trójwymiarowym wektorem położenia jej środka masy.
Środki masy 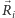 poszczególnych komórek możemy teraz obliczyć, korzystając ze wzoru (1) we współrzędnych odwzorowania, a następnie przeliczyć z powrotem do trójwymiarowych współrzędnych kartezjańskich. Z uwagi na dowolność wyboru odwzorowania skorzystanie z odwzorowania wiernopowierzchniowego (np. odwzorowania Albersa) pozwoli nam na dokładne wyznaczenie pól powierzchni komórek niezależnie od ich rozmiaru i kształtu. Dodatkowo, jeśli rozmiary komórek będą odpowiednio małe (czyli przy odpowiednio dużym
poszczególnych komórek możemy teraz obliczyć, korzystając ze wzoru (1) we współrzędnych odwzorowania, a następnie przeliczyć z powrotem do trójwymiarowych współrzędnych kartezjańskich. Z uwagi na dowolność wyboru odwzorowania skorzystanie z odwzorowania wiernopowierzchniowego (np. odwzorowania Albersa) pozwoli nam na dokładne wyznaczenie pól powierzchni komórek niezależnie od ich rozmiaru i kształtu. Dodatkowo, jeśli rozmiary komórek będą odpowiednio małe (czyli przy odpowiednio dużym 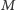 ), wpływ zastosowanego odwzorowania na wyznaczone środki masy
), wpływ zastosowanego odwzorowania na wyznaczone środki masy 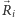 będzie zaniedbywalny, co w prosty sposób zweryfikujemy, badając, czy wyniki zmieniają się wraz ze zmianą np. punktu centralnego odwzorowania.
będzie zaniedbywalny, co w prosty sposób zweryfikujemy, badając, czy wyniki zmieniają się wraz ze zmianą np. punktu centralnego odwzorowania.

Ponieważ badany obszar 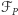 jest dość skomplikowany (jego brzeg składa się z ponad 73000 wierzchołków), nie możemy na nim w prosty sposób określić siatki numerycznej. Wprowadzimy zatem obszar
jest dość skomplikowany (jego brzeg składa się z ponad 73000 wierzchołków), nie możemy na nim w prosty sposób określić siatki numerycznej. Wprowadzimy zatem obszar 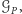 będący prostokątem we współrzędnych rzutowania
będący prostokątem we współrzędnych rzutowania 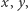 takim, że
takim, że 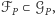 a więc zawierającym w całości projekcję badanej figury
a więc zawierającym w całości projekcję badanej figury 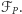 Tak zdefiniowany prostokątny obszar możemy w dowolny sposób podzielić na
Tak zdefiniowany prostokątny obszar możemy w dowolny sposób podzielić na 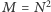 mniejszych, prostokątnych komórek
mniejszych, prostokątnych komórek 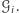
Dla każdej prostokątnej komórki 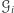 ograniczającego obszaru
ograniczającego obszaru 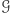 możemy wyznaczyć obszar komórki
możemy wyznaczyć obszar komórki 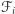 (która niekoniecznie musi być prostokątem) na płaszczyźnie jako
(która niekoniecznie musi być prostokątem) na płaszczyźnie jako 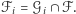 Dla każdej komórki
Dla każdej komórki 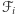 musimy następnie odpowiedzieć na dwa pytania: (a) jakie jest położenie środka masy
musimy następnie odpowiedzieć na dwa pytania: (a) jakie jest położenie środka masy 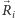 danej komórki, oraz (b) jakie jest pole powierzchni
danej komórki, oraz (b) jakie jest pole powierzchni 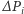 danej komórki. Następnie na podstawie wzoru (2) obliczamy położenie środka masy obszaru
danej komórki. Następnie na podstawie wzoru (2) obliczamy położenie środka masy obszaru 
Warto zauważyć, że jeśli zakładamy, że pomiędzy zdefiniowanymi punktami granica Polski biegnie po linii prostej, to chcielibyśmy, aby linie proste na elipsoidzie (geodezyjne) były również liniami prostymi w naszym wybranym odwzorowaniu. Dla zastosowanego tu odwzorowania wiernopowierzchniowego nie jest to, ściśle mówiąc, spełnione, lecz z uwagi na to, że dane CODGiK zdefiniowane są na bardzo drobnej siatce (średnia odległość pomiędzy sąsiednimi punktami granicznymi wynosi 49 m), nie ma to istotnego wpływu na wynik.
Wyniki
Do wykonania obliczeń posłużył program komputerowy napisany w C++ z użyciem biblioteki GeographicLib (do przeliczania współrzędnych) oraz biblioteki boost::geometry do obliczeń geometrycznych na płaszczyźnie. Dla zminimalizowania wpływu błędów numerycznych przyjęto przekształconą postać wzoru (2):
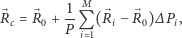 |
(3) |
gdzie za  wybrano arbitralny punkt leżący wewnątrz obszaru
wybrano arbitralny punkt leżący wewnątrz obszaru 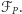 Można łatwo sprawdzić, że wybór tego punktu, jak również wybór punktu centralnego dla odwzorowania Albersa, nie ma istotnego wpływu na wynik.
Można łatwo sprawdzić, że wybór tego punktu, jak również wybór punktu centralnego dla odwzorowania Albersa, nie ma istotnego wpływu na wynik.
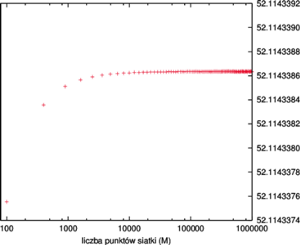
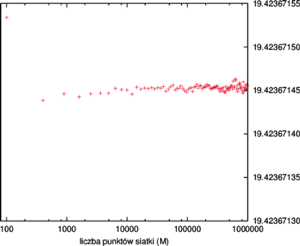
W celu oszacowania niepewności otrzymanego wyniku wykonamy szereg obliczeń dla wzrastającej wartości 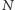 aż do 1000 (co odpowiada
aż do 1000 (co odpowiada 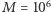 komórek siatki).
komórek siatki).
|
|
Wyniki przedstawiają wykresy na rysunku 3 Z dokładnością rzędu 1 metra środek (masy) obszaru administracyjnego Polski znajduje się we współrzędnych

Powyższy punkt znajduje się w pasie nieużytków nad rzeką Bzurą, na granicy gminy Piątek (powiat łęczycki) i gminy Krzyżanów (powiat kutnowski). Wspomniana uprzednio miejscowość Piątek znajduje się około 6 kilometrów na południowy wschód od wyznaczonego punktu, co i tak jest wyjątkowo dobrym wynikiem, biorąc pod uwagę stopień uproszczenia początkowej metody.
Niejako efektem ubocznym obliczeń jest uzyskanie całkowitego pola powierzchni badanego obszaru, czyli 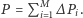 Z uwagi na to, że zastosowano odwzorowanie wiernopowierzchniowe, otrzymana wartość
Z uwagi na to, że zastosowano odwzorowanie wiernopowierzchniowe, otrzymana wartość  jest niezależna od wybranego
jest niezależna od wybranego  i w pełni zgodna z oficjalnie publikowaną wartością (wedle Małego Rocznika Statystycznego Polski 2017).
i w pełni zgodna z oficjalnie publikowaną wartością (wedle Małego Rocznika Statystycznego Polski 2017).
Co dalej?
Co jakiś czas zdarzają się drobne korekty granic, wywołane zarówno przyczynami naturalnymi (np. zmiana biegu rzek), jak i urzędowymi (np. planowana korekta granic z Czechami o 3, 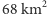 ). Spróbujmy oszacować, jaki wpływ mają takie niewielkie korekty na położenie wyznaczonego przez nas środka. Załóżmy, że do obszaru
). Spróbujmy oszacować, jaki wpływ mają takie niewielkie korekty na położenie wyznaczonego przez nas środka. Załóżmy, że do obszaru 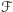 o polu powierzchni
o polu powierzchni 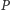 został dołączony fragment
został dołączony fragment 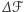 o polu powierzchni
o polu powierzchni 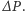 Wychodząc ze wzoru (2), wzór na zmodyfikowane położenie środka
Wychodząc ze wzoru (2), wzór na zmodyfikowane położenie środka 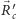 obszaru
obszaru 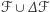 możemy zapisać jako
możemy zapisać jako
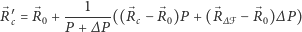 |
co poprzez przyjęcie 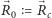 (gdzie
(gdzie 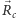 jest środkiem masy obszaru
jest środkiem masy obszaru  ) przyjmuje postać
) przyjmuje postać
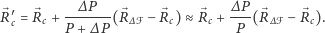 |
Zmiana położenia środka jest zatem proporcjonalna do odległości pomiędzy dotychczasowym położeniem środka a obszarem dołączanym, a także proporcjonalna do stosunku powierzchni obu obszarów. Dla planowanej korekty granic z Czechami 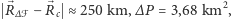 więc po takiej przykładowej korekcie położenie środka Polski przesunie się o około
więc po takiej przykładowej korekcie położenie środka Polski przesunie się o około
 |
Krótko mówiąc - nám to nevadí.
 komórek w siatce numerycznej.
komórek w siatce numerycznej.