W zasadzie wszystkie prawa fizyki można zapisać w postaci układów równań różniczkowych. Wiele modeli biologicznych także daje się przedstawić w postaci układów równań różniczkowych. W tym miejscu trzeba podkreślić, że stany obiektów mogą być tylko w najprostszych przypadkach charakteryzowane za pomocą liczb rzeczywistych. Jest tak, na przykład, gdy obiektem naszych zainteresowań jest populacja komórek znajdujących się w jakimś naczyniu w wodnym roztworze, i interesuje nas, ile komórek znajduje się w jednostce objętości, np. mililitrze wody zaczerpniętej z tego naczynia. Jeśli jednak komórki w naczyniu są rozmieszczone nieregularnie, tak że ich lokalne zagęszczenia w różnych miejscach są różne, to wtedy stan takiej populacji w danej chwili lepiej oddaje funkcja określająca rozkład przestrzenny gęstości komórek w całym naczyniu, a nie liczba, która jest średnią wartością gęstości. By opisać tego typu procesy, stosuje się równania różniczkowe cząstkowe, zawierające pochodne cząstkowe funkcji, które określają, jak bardzo funkcja zmienia się w kierunkach wyznaczonych przez osie układu współrzędnych. Bardzo wiele modeli matematycznych konstruuje się w celu wyjaśnienia powstawania różnych form i kształtów powstających z żywych organizmów tworzących grupy. Tego typu efekty uważa się za przejawy samoorganizacji, ale nie ma w tym nic metafizycznego i wiele z tych zjawisk można zrozumieć poprzez badanie nieliniowych modeli matematycznych.

Jednym z takich modeli, który od ponad 50 lat z różną intensywnością przyciąga uwagę matematyków, jest układ Patlaka-Keller-Segela opisujący zjawisko chemotaksji, powszechnie występujące w przyrodzie. Taksja to ukierunkowany ruch organizmu żywego w kierunku jakiegoś źródła sygnału. Jeśli źródłem jest światło - mówimy o fototaksji, jeśli jakiś związek chemiczny - mamy do czynienia z chemotaksją. Szczególnie interesujący jest przypadek, gdy ów sygnałowy związek chemiczny, zwany atraktantem, ukierunkowuje ruch tych samych indywiduów, które są zdolne do jego emisji. Najbardziej znanym organizmem, u którego zaobserwowano tego typu efekt, jest Dictostelium discoideum, śluzowiec, który w warunkach dostatecznej obfitości związków odżywczych żyje w postaci osobnych komórek.

Spadek poziomu związków odżywczych uruchamia, oparty o chemotaksję, proces gromadzenia się komórek i tworzenia agregatów zawierających nawet po kilkaset komórek, które po pewnym czasie różnicują się do tego stopnia, że ów agregat komórkowy nabiera cech autonomicznego organizmu przypominającego pełzającego ślimaka. Nas jednak interesuje początek tego złożonego procesu - powstawanie agregatów i tu z pomocą przychodzi model Patlaka-Keller-Segela. Jest to układ dwóch równań różniczkowych cząstkowych

gdzie 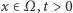to czas, 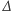to operator dyfuzji, a 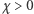parametr określający intensywność chemotaksji. Układ uzupełniamy o warunek początkowy dla 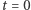oraz warunek izolacji na brzegu obszaru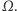

Układ ten omówimy, wskazując, co opisują poszczególne jego człony. Pierwsze równanie opisuje zmiany w czasie gęstości komórek wywołane przez swobodną dyfuzję oraz ruch w kierunku wzrastającej gęstości atraktanta. Drugie równanie opisuje dyfuzję atraktanta 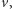jego degradację oraz, przede wszystkim, jego emisję przez komórki. Rzecz jasna tam, gdzie jest więcej komórek, tam większa emisja atraktanta, a więc silniejszy sygnał wskazujący kierunek ruchu dla pozostałych komórek.

W tym miejscu zaczyna się matematyka. Dodajmy tylko, że poszukujemy takich par funkcji 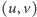określonych na tym samym obszarze 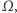które są rozwiązaniami tego układu równań oraz spełniają warunek całkowitej izolacji, tzn. przez brzeg zbioru 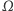nic nie wpływa ani nie wypływa. (Zatem całkowita masa komórek jest stała i równa masie początkowej.) Zgodnie z oczekiwaniami istnieją takie rozwiązania tego układu, które reprezentują wzrost gęstości komórek w otoczeniu określonych punktów zbioru 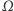- to są właśnie te agregaty, których tworzenie chcemy opisać, ale rozwiązania okazują się mieć zdumiewające własności. Jeśli obszar 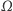jest odcinkiem, to rozwiązania określone są dla wszystkich czasów 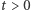i dążą do stanów równowagi. Jeśli początkowo w okolicy pewnego punktu gęstość komórek była dostatecznie duża, będzie ona wzrastać, aż do utworzenia w tym miejscu wąskiej wysokiej górki o wygładzonym szczycie. Jeśli początkowo nie było dostatecznie dużych skupisk komórek, dyfuzja wygrywa i gęstości i 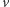dążą do funkcji stałych, niwelując po drodze wszystkie górki i dołki gęstości. Sytuacja zmienia się radykalnie, gdy zbiór 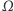jest podzbiorem płaszczyzny lub przestrzeni trójwymiarowej. Można udowodnić, że w przypadku podzbioru płaszczyzny los rozwiązania zależy od masy początkowej komórek. Jeśli jest zbyt duża, to rozwiązanie "żyje" jako funkcja o wartościach rzeczywistych do pewnej chwili wyznaczającej maksymalny czas istnienia 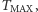zależny od danych początkowych. Co się dzieje? Formuje się taka wąska, coraz wyższa górka, ale jej szczyt, początkowo wygładzony, staje się coraz ostrzejszy, gdy czas zbliża się do 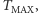aż przestaje być funkcją o wartościach rzeczywistych.

Ale czy to naprawdę koniec? Tak, w pewnym sensie doszliśmy do kresu stosowalności naszego modelu, a efekt, który tu opisujemy, nazywa się nawet wybuchem rozwiązania użytym w tytule tego artykułu. Matematyka jednak przekracza granice naszej wyobraźni, ukazując szerszą klasę rozwiązań, które wprawdzie nie są funkcjami o wartościach rzeczywistych, ale wciąż są funkcjami czasu o wartościach w szerszym zbiorze, zwanym przestrzenią miar. Ale wróćmy do naszego układu równań Patlaka-Keller-Segela. Dlaczego efekt wybuchu rozwiązań tego samego układu równań nie występuje nigdy w przypadku jednowymiarowej dziedziny, ale może występować w przypadku dwóch lub trzech wymiarów? Bez skomplikowanej analizy dostępnej dla specjalistów trudno to wyjaśnić, ale można spekulować, że jest to jakoś związane z tym, że osobliwość będąca przyczyną wybuchu w dwuwymiarowej przestrzeni ma istotnie więcej miejsca do uformowania się niż w przypadku jednowymiarowym.