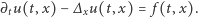Miliony niewiadomych wokół nas

Każdy wie, jak rozwiązywać układ dwóch równań liniowych z dwiema niewiadomymi, np.

Rozwiązanie układu trzech czy czterech równań również nie powinno sprawiać większego kłopotu - wszak łatwo sprowadzić go do rozwiązywania układu/układów dwóch równań. Ale jeśli musielibyśmy rozwiązać... układ miliona równań, z tyluż niewiadomymi?!

gmsh.info

Rozkład naprężeń w kadłubie samolotu poznamy tym lepiej, im gęstsza będzie siatka punktów.

Skąd biorą się tak wielkie układy?

Precyzyjna prognoza pogody, wycena niektórych egzotycznych opcji finansowych, modelowanie wzrostu komórek nowotworowych lub rozwoju epidemii, projektowanie ultranowoczesnych kosmetyków, rozwój tanich żarówek LED, czy samochodów o niskiej emisji - te przykłady można mnożyć - są uzależnione od możliwości przeprowadzenia złożonych symulacji komputerowych modeli matematycznych sformułowanych w języku równań różniczkowych cząstkowych.

Aby rozwiązywać takie równania na komputerze, zwykle przybliża się je za pomocą zestawu wartości na siatce punktów (lub, w metodzie elementu skończonego, przez zestaw prościutkich elementów). Jest intuicyjnie jasne, że jeśli chcemy mieć dokładniejszy wynik, musimy wziąć pod uwagę więcej punktów siatki, czyli wyznaczyć więcej wartości. Niestety, gdy modelowany obiekt jest trójwymiarowy, liczba potrzebnych punktów szybko rośnie: już dla zwyczajnej sześciennej kostki wzięcie zaledwie 100 punktów w każdym kierunku daje w rezultacie 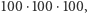czyli milion punktów, a tym samym - milion wartości do wyznaczenia!

Dziesiątki tysięcy procesorów w szafie

Trudne zadanie obliczeniowe wymaga dostatecznie silnego komputera - najlepiej: komputera równoległego - czyli takiego, który składa się z wielu jednocześnie pracujących procesorów. Współczesna technologia przenosi równoległość także na poziom samego procesora, umieszczając w jednym procesorze kilka jednocześnie pracujących rdzeni obliczeniowych.

Jednak co innego mieć potencjał obliczeniowy, a co innego móc go efektywnie wykorzystać. Sytuacja jest podobna jak w ogranym zadaniu o kopaniu studni: jeśli jeden robotnik kopie studnię w 10 godzin, to w jakim czasie wykopie ją dwóch? A stu? A dziesięć tysięcy??? No właśnie... rzecz w tym, że wcale nie jest łatwo zrównoleglić zadanie kopania wąskiej studni. Dokładnie ten sam problem mamy w obliczeniach numerycznych na wielkich komputerach: aby mogły w pełni wykorzystać swoje możliwości, metoda kopania studni musi być bardzo specyficzna - albo zadanie musi być inne.

W niektórych przypadkach faktycznie łatwo sobie wyobrazić, jak można dobrze podzielić zadanie. Na przykład, wyznaczając rozkład naprężeń w napędzie roweru, lub temperatury we wchodzącym w atmosferę statku kosmicznym, wystarczy podzielić obiekt na mniejsze części i w każdym kawałku niezależnie znaleźć rozkład temperatury. Takie podejście nazywa się w numeryce dekompozycją obszaru.

Jednak w tym rozumowaniu jest haczyk: żeby znaleźć temperaturę wewnątrz każdego kawałka, trzeba też znać temperaturę na jego brzegu... A skoro dla przecinających się kawałków przyjmuje te same wartości, to - na pierwszy rzut oka - uniemożliwia niezależne wyznaczenie temperatury na każdym z nich.

Na szczęście jest kilka sposobów ominięcia tej trudności; jeden został zaproponowany w 1869 roku (rzecz jasna, w zupełnie innym kontekście) przez niemieckiego matematyka, Hermanna Schwarza: zamiast poszukiwać rozwiązania wprost, należy do skutku je poprawiać, wielokrotnie powtarzając (czyli, mówiąc fachowo, iterując) ten sam schemat, który obecnie nazywamy naprzemienną metodą Schwarza (obok znajduje się jej opis).

Dwóch panów z ołówkami

Stosując naprzemienną metodę Schwarza i rozwiązując zadanie na kolejnym sąsiednim kawałku, należy uwzględnić świeżo wyznaczone wartości z poprzednich kawałków: tylko wtedy taka iteracja będzie zbieżna. To jednak nie pozwala szukać rozwiązań na wszystkich kawałkach jednocześnie - i tym samym poważnie psuje równoległość algorytmu...

Przełom przyszedł w 1987 roku, gdy w raporcie Courant Institute dwóch matematyków: Maksymilian Dryja z Uniwersytetu Warszawskiego i Olof Widlund z Uniwersytetu Nowojorskiego, zaproponowało zaskakujące uproszczenie metody.

Rozwiązujmy zadania we wszystkich kawałkach jednocześnie, a wartości na zakładkach bierzmy po prostu z poprzedniej iteracji! Na zakończenie każdej iteracji kawałki rozwiązania sklejamy, dodając poprawki. W ten sposób najkosztowniejsza część metody - rozwiązywanie równania na kawałkach - może wykonać się w pełni równolegle. Odwaga podejścia Dryji i Widlunda polegała na tym, że tak pomyślana iteracja nie musi być zbieżna do dokładnego rozwiązania, jednak... to nic nie szkodzi. Bo nie będzie wykorzystana wprost do rozwiązywania równania, tylko jako potężny akcelerator dla innej, prostej (i zazwyczaj bardzo wolno działającej) metody. Sprytnie łącząc ze sobą dwie metody iteracyjne: wcale nie zbieżną oraz kiepsko zbieżną, otrzymali - co zostało udowodnione w wymienionym wcześniej raporcie - metodę zbieżną, i to bardzo szybko.

Trzeba działać i lokalnie, i globalnie

W tej beczce miodu jest łyżka dziegciu, z czego już wtedy zdawali sobie sprawę Dryja i Widlund - i od razu podali sposób jej neutralizacji. Znów łatwiej będzie nam odwołać się do fizycznej intuicji.

Rozważmy długi pręt, który podgrzewamy na jednym z końców. Gdy podzielimy pręt na 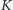małych, zachodzących na siebie kawałków i będziemy prowadzić iterację addytywnej metody Schwarza, to informacja o tym, że pierwszy kawałek jest podgrzewany, dotrze do ostatniego dopiero po 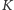iteracjach - a przecież podgrzewanie pręta z jednego końca zmienia jego temperaturę wszędzie. Dlatego można spodziewać się - i faktycznie tak jest - że nasza metoda będzie działać tym gorzej, im więcej będzie kawałków, na które podzielimy interesujący nas obiekt: bo wymiana informacji między odległymi od siebie kawałkami będzie wymagać coraz więcej czasu.

Lekarstwem jest dodanie (w końcu to metoda addytywna...) mechanizmu przyspieszającego transfer informacji - choćby mało dokładnej - o zachowaniu się rozwiązania w każdym z kawałków obiektu. Jest to konieczne, o ile chcemy zachować efektywność metody także wtedy, gdy obiekt zostaje podzielony na dziesiątki tysięcy części, z których każdą będziemy rozwiązywać na innym procesorze.

Konstrukcja tego mechanizmu nie zawsze jest oczywista i mimo że przez ostatnich 30 lat wiele w tej sprawie już zrobiono, na horyzoncie wciąż pojawiają się nowe pytania - także dlatego, że zmienia się architektura komputerów równoległych i zmieniają się zadania, jakie chcemy rozwiązywać.

Liczba niewiadomych wciąż rośnie

Choć w roku, kiedy metodę wymyślono, za masywnie równoległy uważano każdy komputer, który miał aż(!) 16 procesorów, dziś addytywna metoda Schwarza pozwala rozwiązywać jedne z najtrudniejszych problemów obliczeniowych, gdy rutynowo uruchamia się symulacje na komputerach mających tysiące procesorów.

Nieprzypadkowo nagrodę Gordona Bella za rok 2016 (zob. awards.acm.org/bell) przyznano za przeprowadzenie na największym komputerze świata, Sunway TaihuLight, symulacji na potrzeby prognozowania pogody, wymagającej rozwiązywania układów równań zawierających aż 770 miliardów niewiadomych. Jej jądrem obliczeniowym była (w wersji RAS, która dodatkowo ogranicza komunikację między procesorami) właśnie addytywna metoda Schwarza.

To oczywisty dowód na to, że nasza trzydziestolatka jest wciąż pełna wigoru!