Pierwsze cyfry
Rozważmy następujący problem: gromadzimy powierzchnie wszystkich krajów wyrażone w kilometrach kwadratowych i patrzymy tylko na pierwsze cyfry znaczące tych wartości. Otrzymamy listę liczb z zakresu od 1 do 9 włącznie; pytanie brzmi, jakie są częstości ich występowania w tym zbiorze?
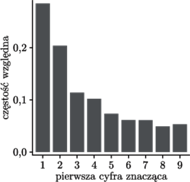
Rys. 1 Rozkład częstości pierwszych cyfr znaczących powierzchni wszystkich krajów świata
W dobie powszechnego i otwartego dostępu do informacji nietrudno sprawdzić to samemu; jeżeli umieścimy częstości na wykresie, będzie on przypominać rysunek 1.
Czy regularny kształt tego wykresu to tylko ciekawy przypadek, czy jesteśmy na tropie ogólnej zależności (którą najchętniej opisalibyśmy wzorem)? Uważny Czytelnik zapewne spostrzegł, że formułując problem, poczyniliśmy pewne założenie, mianowicie chcieliśmy, żeby powierzchnie krajów były wyrażone w kilometrach kwadratowych. Jednak nie wszystkie kraje na świecie używają systemu metrycznego - czy kształt rozkładu zmieni się, jeżeli wyrazimy je w milach kwadratowych lub stopach kwadratowych? Co będzie, jeżeli spojrzymy na ludność zamiast na powierzchnię, albo historyczne wartości ludności?
Wreszcie, czy musimy ograniczać się do danych geograficznych? Absolutnie nie! Spójrzmy więc na pierwsze 1000 wyrazów ciągu Fibonacciego, liczby (niebędące datami bądź liczbami porządkowymi, numerami stron, itd.) pojawiające się w dowolnym wydaniu Financial Timesa albo w dowolnej pracy naukowej z dużą ilością danych liczbowych.
Pozostawię to tutaj jako ćwiczenie z wyszukiwania informacji dla chętnych, ale zdradzę, że wynik (oczywiście w przybliżeniu) jest zawsze taki sam.

Rys. 2 Rozkład częstości powierzchni krajów (a) w skali liniowej, (b) w skali logarytmicznej na osi X, (c) pojedynczy rząd wielkości z (b), (d) przybliżenie, liczby w zakolorowanym obszarze zaczynają się od 1
Aby zrozumieć, co się dzieje, musimy odwołać się do rozkładu całych liczb (rysunek 2), ale zamiast mało informatywnej skali liniowej (a) na osi poziomej użyjemy skali logarytmicznej (b). Patrząc tylko na jeden rząd wielkości, tj. wartości pomiędzy dwiema kolejnymi potęgami dziesiątki (c) (liczby w kolejnych obszarach rozpoczynają się od 1, 2, i tak dalej), widzimy, że te obszary stają się coraz mniejsze.
Jeśli założymy, że wśród liczb wewnątrz jednego rzędu wielkości ten rozkład nakreślony w skali logarytmicznej na osi poziomej jest w przybliżeniu stały (d), to pole zakolorowanego obszaru będzie równe: 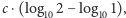 a ogólnie, dla dowolnej cyfry początkowej
a ogólnie, dla dowolnej cyfry początkowej 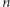 będzie to
będzie to
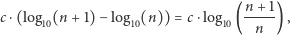
czyli względna częstość cyfry początkowej  to po prostu
to po prostu
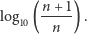
Ta sama prawidłowość zachodzi dla wielu rodzajów zbiorów liczb (m.in. tych wymienionych powyżej), jednak łatwo przywołać przykłady, dla których nie zachodzi, np. wzrost, masa ciała ludzi.
Aby wyjaśnić, co wyróżnia wymienione klasy danych liczbowych, musimy odwołać się z powrotem do rysunku 2(b). Po pierwsze, aby nasze przybliżone obliczenia były uzasadnione, dane muszą obejmować kilka kolejnych rzędów wielkości, w praktyce co najmniej 3-4, co wyklucza m.in. wzrost i masę ciała. Ponadto, ponieważ zmiana jednostki (np. z kilometrów kwadratowych na mile kwadratowe, jak w przykładzie z powierzchniami) jest niczym innym jak mnożeniem wszystkich wartości przez stałą, rozkład częstości na skali logarytmicznej zachowuje swój kształt i przesuwa się w lewo lub w prawo. Jeżeli na początku rozkład nie obejmował wystarczająco wielu rzędów wielkości bądź nie był wystarczająco "płaski" na skali logarytmicznej, przeliczenie jednostki sprawi, że proporcje wielkości zakolorowanych obszarów ulegną zmianie, tym samym zmieniając kształt rozkładu częstości pierwszych cyfr.
Opisana prawidłowość jest nazywana prawem Benforda, mimo że Frank Benford nie był pierwszą osobą, która zauważyła to zjawisko. Pierwszy był Simon Newcomb, znany również ze swojej pracy w dziedzinach fizyki, astronomii i ekonomii, który w roku 1881 zauważył, że w tablicach logarytmicznych w bibliotece strony z liczbami zaczynającymi się od 1 były bardziej zużyte od tych z liczbami zaczynającymi się od 2, itd. Odkrycie popadło w zapomnienie aż do roku 1938, kiedy Frank Benford, inżynier i fizyk pracujący dla General Electric, opublikował swoje obserwacje poparte przykładami wielu różnych zbiorów liczbowych spełniających zależność, m.in. tych wartości geograficznych, od których rozpoczęliśmy nasze rozważania.

Rys. 3 Fragment przybliżonego rozkładu częstości liczb spełniających prawo Benforda na skali logarytmicznej
Szukając możliwych uogólnień tego zjawiska, zastanówmy się, czy dla wartości liczbowych, których pierwsze cyfry zachowują się zgodnie z rozkładem Benforda, da się coś powiedzieć o drugich i kolejnych cyfrach tych liczb. Otóż tak, spójrzmy na rysunek 3, podobny do rysunku 2(d), ale z innymi zakolorowanymi obszarami.
Podobnie jak wyznaczaliśmy obszary obejmujące liczby zaczynające się od 1, możemy wyznaczyć obszary, w których znajdują się liczby zaczynające się od 12, 22, 32, itd., czyli wszystkie, w których drugą cyfrą znaczącą jest 2. Jeżeli oznaczymy dowolny ciąg cyfr jako 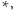 dowolną pojedynczą cyfrę jako
dowolną pojedynczą cyfrę jako 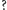 i prawdopodobieństwo tego, że liczba zaczyna się od ciągu dwóch cyfr
i prawdopodobieństwo tego, że liczba zaczyna się od ciągu dwóch cyfr 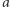 i
i 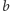 jako
jako 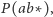 to podobnie jak poprzednio, biorąc pod uwagę powierzchnię obszaru obejmującego liczby rozpoczynające się od 12, możemy określić
to podobnie jak poprzednio, biorąc pod uwagę powierzchnię obszaru obejmującego liczby rozpoczynające się od 12, możemy określić
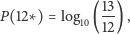
czyli - sumując po wszystkich możliwych pierwszych cyfrach - mamy
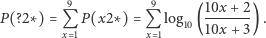
Wzór ogólny dla drugiej cyfry znaczącej 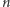 przybiera następującą formę:
przybiera następującą formę:
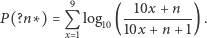
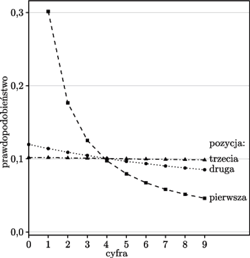
Rys. 4 Prawdopodobieństwo wystąpienia danej cyfry na kolejnych pozycjach liczby ze zbioru spełniającego prawo Benforda
Idąc dalej, możemy łatwo otrzymać wzór na prawdopodobieństwo 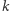 -tej cyfry równej
-tej cyfry równej  ; nietrudno zauważyć, że przy rosnącym numerze cyfry
; nietrudno zauważyć, że przy rosnącym numerze cyfry 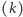 rozkład prawdopodobieństwa bardzo szybko staje się nierozróżnialny od rozkładu równomiernego (rysunek 4).
rozkład prawdopodobieństwa bardzo szybko staje się nierozróżnialny od rozkładu równomiernego (rysunek 4).
Prawo Benforda można też uogólnić na inne systemy liczbowe, we wzorach zamieniamy wtedy podstawę logarytmu i wszelkie dziesiątki na podstawę systemu liczbowego, którego używamy. Liczby spełniające zależność w jednym systemie liczbowym będą ją dalej spełniać po zamianie podstawy.
Na koniec, zainteresowanym dowodem, tudzież formalnym wyjaśnieniem tego empirycznego zjawiska, polecam serię artykułów Theodore'a P. Hilla. W tych publikacjach autor opisuje, jak generowanie liczb losowych ze zbioru wielu różnych losowych rozkładów prawdopodobieństw w naturalny sposób prowadzi do rozkładu Benforda dla ich kolejnych cyfr znaczących.