Trudne pytania

Jednym z podstawowych zadań statystyki jest estymacja wskaźnika struktury, albo mówiąc inaczej, szacowanie odsetka osób (elementów, obiektów) charakteryzujących się pewną cechą, będącą przedmiotem prowadzonego badania. Przykładowo, może nas interesować, jaki procent dorosłych obywateli naszego kraju ma prawo jazdy, jaki odsetek dzieci i młodzieży w wieku szkolnym umie pływać itd.

Zauważmy, że w obu wspomnianych przykładach mamy do czynienia z cechą o charakterze binarnym, tzn. dopuszczamy tylko dwie wykluczające się odpowiedzi: ktoś ma prawo jazdy albo go nie ma; umie pływać albo nie umie.

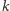Rozwiązanie tak postawionego zadania jest stosunkowo proste: ankieterzy zadają pytania losowo wybranej grupie osób i zliczają odpowiedzi twierdzące. Jeżeli symbolem $n$ oznaczymy liczbę wszystkich uzyskanych odpowiedzi, pośród których $k$ brzmiało "tak", wówczas interesujący nas odsetek osób obdarzonych badaną cechą szacujemy za pomocą ilorazu (ewentualnie mnożonego przez 100%):

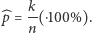k p =--(⋅100%). n

(1)

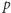Litera $p$ użyta we wzorze (1) oznacza prawdopodobieństwo tzw. sukcesu (czyli uzyskania odpowiedzi "tak" na zadane pytanie), natomiast dodanie "daszka" nad 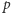$|p$ jest tradycyjnie stosowanym oznaczeniem informującym, iż mamy do czynienia z oszacowaniem 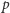$p$ (lub, mówiąc bardziej formalnie, z estymatorem wartości $p$ ).

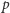Można wykazać, że ten - zdawałoby się banalny - estymator prawdopodobieństwa sukcesu ma bardzo dobre własności matematyczne: m.in. jest nieobciążony (tzn. wolny od błędu systematycznego), zgodny (tzn. dostarcza oszacowanie dowolnie bliskie prawdziwej wartości parametru, o ile tylko próbka jest dostatecznie liczna) i efektywny (ma możliwie małą wariancję, czyli jest dość precyzyjny). Tak więc, o ile tylko odpowiedzi respondentów są rzetelne, możemy oczekiwać, iż posługując się wzorem (1), uzyskamy rozsądne oszacowanie odsetka osób charakteryzujących się interesującą nas cechą - zwłaszcza jeśli badanie przeprowadzimy na odpowiednio dużej i jednorodnej grupie osób.

Założenie dotyczące rzetelności odpowiedzi bywa zasadniczo spełnione, o ile pytania dotyczą tematów w miarę neutralnych, jak choćby wspomniane wyżej (posiadanie prawa jazdy, umiejętność pływania itp.). Trudno bowiem byłoby wskazać przyczynę, dla której ankietowana osoba w obliczu tego typu pytań miałaby kłamać, zwłaszcza że respondentom zapewnia się anonimowość.

Można jednakże wskazać i takie badania, dotyczące zachowań bądź poglądów odnoszących się zwłaszcza do obyczajowości oraz przestrzegania prawa, gdy oczekiwanie szczerych odpowiedzi od respondentów wydaje się mało prawdopodobne. Są to tzw. trudne pytania typu: Czy brał/dawał pan łapówkę? Czy zażywasz narkotyki? Czy dokonała pani aborcji? Czy zatrudnia pan pracowników "na czarno"? Można spodziewać się, że na takie pytania wielu respondentów w ogóle nie będzie chciało odpowiadać - nawet w obliczu wszelkiego typu gwarancji anonimowości - a jeśli już się zgodzą, to ich wypowiedzi będą niejednokrotnie "politycznie poprawne", ale niekoniecznie prawdziwe. Tym samym, skoro mamy uzasadnione wątpliwości co do liczby uzyskanych odpowiedzi twierdzących (czyli 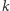$k$ ), użyteczność wzoru (1) staje pod znakiem zapytania. Czy to oznacza, że estymacja w obliczu trudnych pytań sprowadza się do przysłowiowego wróżenia z fusów? Na szczęście nie, bowiem statystycy wymyślili metodę, która z jednej strony doskonale zabezpiecza prywatność respondentów, a z drugiej umożliwia wyciąganie uzasadnionych wniosków. Jak to możliwe?

Wyobraźmy sobie następującą sytuację. Ankieter, zwracając się do respondenta z "trudnym" pytaniem, mówi:

Zdaję sobie sprawę, że wolałby pan nie odpowiadać wprost na to pytanie. Postąpmy zatem następująco: proszę rzucić monetą, ale nie pokazywać mi wyniku rzutu - jeśli wypadnie orzeł, proszę odpowiedzieć uczciwie tak/nie na zadane pytanie, natomiast jeśli wypadnie reszka, proszę odpowiedzieć tak/nie na pytanie, czy numer domu, w którym pan zamieszkuje, jest parzysty.

Zwróćmy uwagę, że w takim postępowaniu ankieter uzyskuje odpowiedź "tak" albo "nie", nie wiedząc jednocześnie, na które z pytań odpowiada respondent.

Wydaje się, że ten sposób pozyskiwania odpowiedzi jest w pełni bezpieczny dla osoby ankietowanej, która przekazuje pewien komunikat, a zarazem w sposób jawny nie odnosi się do zadanego pytania. Czy jednak uzyskane tą drogą dane mogą być istotnie użyteczne dla badacza? Okazuje się, że tak.

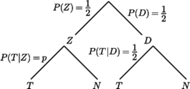
Narysujmy schemat pytań i odpowiedzi w postaci drzewa o wierzchołkach: 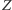$|Z$ - odpowiedź na "trudne" pytanie, 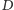$D$ - odpowiedź na pytanie o parzystość numeru domu, 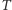$|T$ - tak, 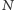$N$ - nie (por. rysunek). Liczby umieszczone nad gałęziami drzewa oznaczają prawdopodobieństwa znalezienia się w poszczególnych wierzchołkach. W szczególności, 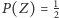$1 P (Z) = 2$ oznacza prawdopodobieństwo, iż respondent odpowiedział na "trudne" pytanie, 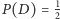$|P(D) = 12$ jest prawdopodobieństwem tego, że wypowiedział się na temat parzystości numeru domu (oba te prawdopodobieństwa są równe 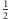$1 |2$ z uwagi na założenie, iż mamy do czynienia z monetą symetryczną), 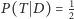$1 P(T D) = 2$ jest prawdopodobieństwem odpowiedzi twierdzącej na pytanie o parzystość numeru domu, natomiast 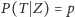$|P(T Z) = p$ oznacza poszukiwane przez nas prawdopodobieństwo odpowiedzi "tak" na interesujące nas pytanie. Jeśli przez 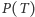$P(T )$ oznaczymy prawdopodobieństwo uzyskania odpowiedzi twierdzącej (bez względu na to, na jakie pytanie odpowiadał faktycznie respondent), to z tzw. wzoru na prawdopodobieństwo całkowite otrzymamy:

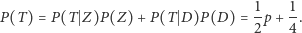1 1 P (T) = P(T Z)P (Z) + P(T D)P (D) =-p+--. 2 4

(2)

Wartość prawdopodobieństwa 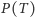$| P (T)$ nie jest, oczywiście, znana, ale prowadząc badanie na 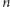$n$ -elementowej próbce respondentów, spośród których 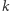$k$ wypowiedziało się twierdząco, możemy oszacować je, korzystając ze znanego nam już wzoru (1). Tym samym wzór (2) możemy zapisać w postaci

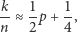k- 1- 1- n ≈ 2p + 4,

(3)

przy czym znak równości przybliżonej przypomina nam, że mamy tu do czynienia z pewnym oszacowaniem na podstawie eksperymentu.

Przekształcając wzór (3), otrzymujemy poszukiwany przez nas estymator odsetka odpowiedzi twierdzących uzyskanych na zadane "trudne" pytanie

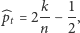p = 2k-− 1, t n 2

(4)

przy czym indeks 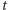$t$ dodaliśmy dla odróżnienia estymatora "trudnych" pytań od powszechnie stosowanego estymatora (1). Estymator (4) ma również przyzwoite własności statystyczne, aczkolwiek - jak można się domyślać - nie aż tak dobre, jak estymator (1), niewymagający dodatkowych zabiegów maskujących odpowiedź. Warto przy tym pamiętać, że jakość estymatora może zależeć od sposobu maskowania. Przykładowo, jeżeli zamiast monety dalibyśmy respondentowi tradycyjną kostkę do gry wraz ze wskazówką, by odpowiadał na nasze pytanie, o ile w wyniku rzutu kostką otrzyma liczbę oczek nie większą niż 4, to - rozumując analogicznie jak poprzednio - otrzymalibyśmy

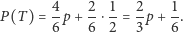
P(T ) = 4-p+-2⋅-1= 2-p+ 1-. 6 6 2 3 6

Po podstawieniu 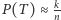$k P (T) ≈ n$ oraz elementarnym przekształceniu otrzymalibyśmy następujący estymator:

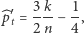
p′ = 3k-− 1, t 2n 4

którego błąd średniokwadratowy jest mniejszy niż błąd estymatora (4). Idąc tym tropem, ktoś mógłby zaproponować mechanizm losowy, który by jeszcze bardziej zwiększał szansę na to, iż respondent odpowiadałby na interesujące nas pytanie, a nie odnosił się do nieistotnej kwestii parzystości numeru domu (np. dla wyników rzutu kostką od 1 do 5 - "trudne" pytanie, 6 - pytanie o parzystość). Jednakże, wbrew pozorom, taki estymator - choć mający lepsze własności matematyczne - w praktyce mógłby okazać się mniej użyteczny niż (4), bowiem respondent mógłby nabrać podejrzeń, że zbyt łatwo da się odkryć, na jakie pytanie odpowiada, co z kolei zniweczyłoby nasze wysiłki.

Czytelnik Uważny z pewnością zwróci uwagę na możliwość manipulowania jeszcze innym parametrem - tym, który związany jest z prawdopodobieństwem udzielenia odpowiedzi twierdzącej w pytaniu obojętnym z punktu widzenia prowadzonego badania. Przykładowo, zamiast pytać o parzystość numeru domu moglibyśmy pytać, czy respondent urodził się w okresie od września do grudnia włącznie itd. (zachęcamy zainteresowanych do prześledzenia wpływu tego parametru na własności estymatora odsetka dla "trudnych" pytań).

Badając teoretyczne własności omawianych estymatorów, nie powinniśmy tracić z pola widzenia ich "praktycznej mocy", którą amerykański statystyk Churchill Eisenhart zdefiniował jako "iloczyn własności matematycznych i prawdopodobieństwa tego, że dana procedura będzie kiedykolwiek zastosowana w praktyce". Doświadczenie pokazuje bowiem, że nazbyt wyrafinowane pomysły nie zawsze spotykają się z zainteresowaniem praktyków, dla których prostota rozwiązania bywa nieraz ważniejsza od niewielkiego zysku z tytułu potencjalnej poprawy jakości. A z tego typu sytuacjami spotykamy się często w naukach społecznych i badaniach, w których istotnym elementem jest tzw. czynnik ludzki. Gdy patrzymy z tej perspektywy, wydaje się, że do szacowania odsetka odpowiedzi twierdzących na "trudne" pytania preferowany będzie właśnie najprostszy estymator (4).