1. Battlestar Galactica - wstępne informacje

By zrozumieć badane zagadnienie, potrzebnych będzie kilka podstawowych informacji o samym serialu i przedstawionym w nim świecie. Czterosezonowy Battlestar Galactica (a właściwie nowa wersja serialu o tym samym tytule z lat 70.) był emitowany w USA w latach 2003-2009 i zdobył olbrzymią popularność - zarówno wśród krytyków (czego wyrazem były najcenniejsze dla twórców seriali nagrody: Emmy i Peabody), jak i wśród publiczności, której głosom zawdzięcza drugie miejsce w rankingu najlepszych seriali science-fiction Entertainment Weekly oraz wysokie miejsca (w pierwszej dziesiątce) w różnych klasyfikacjach najlepszych seriali wszech czasów i wszystkich rodzajów.

Fot. Zdzisław Pogoda

Czy to jest Cylon? Kto wie, ale wizerunki znanych Cylonów są lepiej chronione prawem autorskim.

Sedno fabuły, rozgrywającej się zarówno w przestrzeni kosmicznej, jak i na rozmaitych planetach, nie wydaje się na pierwszy rzut oka zbyt oryginalne (przynajmniej jak na ten gatunek filmowy). Jest nim bunt robotów obdarzonych wysoce rozwiniętą sztuczną inteligencją (zwanych Cylonami) oraz ich walka przeciw ludziom. Serial rozpoczyna się od zniszczenia prawie całej ludzkiej cywilizacji w wyniku nagłego ataku Cylonów. Resztki ludzkości (ok. 50000 uratowanych z katastrofy) walczą o przetrwanie i uciekają przez kosmos przed pościgiem Cylonów, poszukując nowego domu. Floty różnorodnych statków kosmicznych strzeże jedyny ocalały okręt bojowy - tytułowy Battlestar Galactica.

Oryginalnym pomysłem i w rezultacie źródłem napięcia fabularnego, zapewniającego serialowi powodzenie, było, między innymi, "uczłowieczenie" zbuntowanych robotów - i to w sensie dosłownym. Pierwsza, skostruowana przez ludzi i doskonale im znana forma Cylonów przypomina wyglądem rozbudowany toster. Jednakże, dzięki ewoluującej sztucznej inteligencji, Cyloni potrafili przebudować i udoskonalić kolejne swoje kopie tak, by były praktycznie nieodróżnialne od ludzi.

Konsekwencje tego faktu, zarówno dla fabuły, jak i atmosfery serialu są niezwykle doniosłe. Agenci Cylonów, udający ludzi, infiltrują flotę rozbitków, powodując poważne zagrożenie: szerzą fałszywe pogłoski, zdradzają położenie floty pościgowi, dokonują aktów sabotażu i zamachów na przywódców ludzkości itp. Jednocześnie, istnienie cylońskich agentów tworzy jedyną w swoim rodzaju atmosferę podejrzliwości, gdyż każdy z bohaterów serialu może tak naprawdę okazać się wrogiem, przyczyniającym się do klęski pozostałych. Paranoja ta ma dodatkową, głębszą warstwę: ukryci na pokładzie Cyloni mogą nie tylko zachowywać się, myśleć i odczuwać jak ludzie, ale nawet sądzić, że są ludźmi! Dzieje się tak, gdyż dopóki nie zostanie uruchomiony program, według którego dany Cylon działa, nie ma on świadomości swojej natury. Prawdopodobnie ta właśnie niepewność kierująca krokami bohaterów w skrajnie wymagających sytuacjach wyróżnia ten serial wśród wielu innych o podobnej tematyce.

2. Postawienie problemu - wykrywanie agentów

Przedstawiona powyżej sytuacja jest, z perspektywy ludzkiej floty, praktycznie beznadziejna. Rozwiązaniem, jak zwykle w filmach fantastyczno-naukowych, ma być technologia na służbie dziwnie zachowującego się geniusza. W serialu Battlestar Galactica rolę genialnego dziwaka, który ma poradzić sobie z zagrożeniem, pełni Gaius Baltar - wielka osobowość medialna, polityk i playboy, ale przede wszystkim naukowiec. Baltar jest tytułowany doktorem, choć nie wiadomo jakiej nauki - zajmuje się wszelkimi sprawami związanymi z technologią: od informatyki i fizyki po biologię (choć, jak za chwilę się przekonamy, raczej nie jest to matematyk). I właśnie Gaius Baltar skonstruował tzw. detektor Cylonów, czyli urządzenie, które w próbce krwi danej osoby wykrywa substancje charakterystyczne dla Cylonów (jeśli takie istnieją). Wydawałoby się, że problem został rozwiązany, ale... Oddajmy głos samemu Baltarowi:

Plan Baltara: testujemy każdą próbkę z osobna. Przez 61 lat...

Podsumowując: ludzka flota dysponuje bardzo ograniczonymi zasobami - w szczególności tylko jednym stanowiskiem laboratoryjnym i jednym naukowcem wystarczająco kompetentnym, by prowadzić testy. W rezultacie można testować jednocześnie tylko jedną próbkę. Agentów cylońskich we flocie jest niewielu, więc nie będziemy na nich trafiać zbyt często. Baltar planuje po kolei wykonać testy na każdej z próbek, co zajmie tyle czasu, że agenci cylońscy mogliby wielokrotnie zniszczyć flotę, zanim cała procedura się zakończy (i to przy założeniu, że testy mają 100% skuteczności). Nie mówiąc już o tym, że sam Baltar lubi korzystać z uroków życia i nie ma zamiaru spędzić go w laboratorium.

Z tego powodu projekt detektora Cylonów został zakończony i stosowany był tylko do sprawdzania pojedynczych, najbardziej podejrzanych osób. Tymczasem okazuje się, że gdyby Gaius Baltar był lepszym statystykiem (lub miał jakiegoś statystyka do pomocy), mógłby znacząco poprawić oczekiwany czas trwania projektu, zmniejszając go do rozsądnych rozmiarów.

Rozwiązanie problemu Baltara znaleźć możemy w pracy Human or Cylon? Group testing on Battlestar Galactica Christophera R. Bildera, statystyka z Uniwersytetu Nebraska w Lincoln. Opiera się ono na zastosowaniu tzw. testów grupowych.

3. Testy grupowe

Pomysł jest bardzo prosty: jeśli przewidujemy, że Cylonów infiltrujących flotę jest stosunkowo niewielu (a jeśli jest inaczej, to ludzkość i tak może się w zasadzie poddać), to możemy oszczędzić wiele czasu, łącząc "podejrzanych" w grupy i zlewając część próbki krwi każdego członka grupy do jednej, wspólnej próbki. Teraz testujemy każdą z tych grup z osobna. Jeśli taki test da wynik negatywny (tj. brak oznak "cyloństwa"), wiemy, że w danej grupie nie ma Cylona i nie musimy testować każdego członka grupy z osobna (jeśli populację podzieliliśmy na grupy 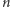-osobowe, to na każdym takim teście oszczędziliśmy sobie 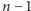testów). Jeśli zaś w jakiejś grupie wynik jest pozytywny, korzystając z niewykorzystanych reszt próbek, testujemy wszystkich członków danej grupy według wcześniejszego planu. Co prawda w tym drugim przypadku wykonujemy jeden nadmiarowy test, ale w sumie i tak to podejście będzie korzystne, gdyż większość wyników będzie negatywnych (z założenia o niewielkiej liczbie Cylonów).

Testy grupowe - pierwsza faza dla grup wielkości 4.

Pomysł ten nie jest w zastosowaniach matematyki niczym nowym. Po raz pierwszy testy grupowe zostały zaproponowane i zastosowane przez Roberta Dorfmana w 1943 r. do badania amerykańskich żołnierzy na frontach II wojny światowej pod kątem chorób zakaźnych. Do dziś metoda jest używana przez Czerwony Krzyż do sprawdzania, czy krew pobrana od krwiodawców nie jest zakażona np. wirusowym zapaleniem wątroby, czy wirusem HIV - wykorzystuje się testowanie grupowe na grupach 16-próbkowych. W ten sposób sam Amerykański Czerwony Krzyż bada 6 milionów próbek rocznie (choć, trzeba przyznać, ma do tego znacznie lepsze warunki niż Baltar). Testowanie grupowe stosuje się też w weterynarii (wykrywanie zakażonych zwierząt podczas epidemii) i tworzeniu lekarstw (eksperymentalne wykrywanie substancji czynnych).

W oczy rzuca się to, że metodę Dorfmana dość łatwo można ulepszyć, zwłaszcza jeśli chodzi o drugą fazę: testy indywidualne. Pierwsza taka poprawka pochodzi od Andrew Sterretta (1957 r.). W grupie, która otrzymała wynik pozytywny, badamy próbki tylko do momentu, gdy otrzymamy wynik pozytywny. Gdy tak się stanie, resztę tej grupy znów testujemy "zbiorowo", co oszczędza nam znowu trochę testów, o ile otrzymamy wynik negatywny, tj. w grupie był tylko jeden Cylon (znów jest to dość prawdopodobne, ze względu na "rzadkość" Cylonów).

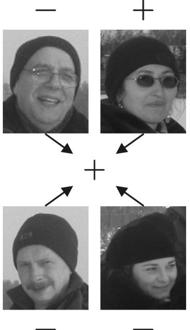
Metoda Sterretta - idea: jeśli przetestujemy najpierw osoby z górnego rzędu, otrzymamy wynik pozytywny u osoby po prawej. Wtedy osoby z dolnego rzędu możemy przetestować grupowo, co zmniejszy o jeden liczbę koniecznych testów.

Jeszcze lepsze wyniki uzyskali Eugene Litvak, Xin Tu i Marcello Pagano w 1994 roku. Zaproponowali oni tzw. metodę połowienia (halving). W każdym kroku grupę "pozytywną" dzielimy na dwie, mniej więcej równe części i każdą z tych części testujemy grupowo, a następnie wybieramy kolejną, mniejszą grupę "pozytywną", aż dojdziemy do jednej osoby. Na przykład, jeśli mamy grupę 8 próbek, które dają razem pozytywny wynik badania, dzielimy ją na dwie czwórki i je testujemy. Następnie wybieramy czwórkę, która dała wynik pozytywny, dzielimy ją na dwie dwójki i testujemy te dwójki, aż wreszcie dwójkę, która da wynik pozytywny, testujemy indywidualnie. Wartość oczekiwana liczby prób koniecznych do znalezienia wszystkich pozytywnych próbek w tym przypadku jest znacznie mniejsza niż w metodzie Sterretta, nie mówiąc o metodzie Dorfmana.

Metoda macierzowa: na czerwono zaznaczone wiersz i kolumna, których testy dały wynik pozytywny, oraz wskazana przez te testy próbka.

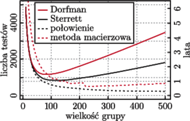
Wykres oczekiwanej liczby koniecznych do wykonania testów w zależności od wyboru wielkości grup testowych.

Istnieją również metody testowania grupowego, które nie opierają się na prostym podziale na grupy i są mniej więcej równie efektywne, jak wymienione wcześniej. Wyróżnia się spośród nich metoda macierzowa, opracowana przez Raviego Phatarfoda i Aidana Sudbury'ego w 1994 roku. Próbki układamy w postaci dużej tablicy i grupowo testujemy wszystkie jej wiersze oraz wszystkie jej kolumny. Przecięcia wierszy i kolumn, które dały wyniki pozytywne, wskazują próbki "podejrzane". Wystarczy je przetestować indywidualnie, by znaleźć te, o które chodziło.

4. Testy grupowe a wykrywanie Cylonów

Czy testy grupowe faktycznie pomogłyby Baltarowi w wykryciu Cylonów? Pamiętajmy, że opłaca się je stosować tylko w przypadku, gdy liczba próbek pozytywnych w stosunku do całej populacji jest niewielka. Z dalszych odcinków serialu można się dowiedzieć, że w momencie podjęcia badań przez Baltara we flocie przebywało 7 cylońskich agentów, a zatem ten stosunek wynosił 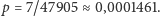Z kolei z danych Amerykańskiego Czerwonego Krzyża wynika, że częstość występowania próbek krwi zarażonych wirusem HIV wynosi 0,0000975, czyli jest mniej więcej taka sama. Na potrzeby Czerwonego Krzyża testy grupowe były idealne, więc i doktorowi Baltarowi mogłyby się przydać.

Szczegółowe oszacowania skuteczności poszczególnych metod można odczytać z wykresu na marginesie.

Jak widać, najlepsze wyniki daje metoda połowienia: tylko 221 testów (101 dni) dla grup wielkości 500 i zaledwie 172 testy (ok. 79 dni) dla grup wielkości 4080. Najprymitywniejsza metoda Dorfmana osiąga swoje optimum przy grupach wielkości 80 i wymaga wykonania 1156 testów (czyli 1,5 roku), co nadal daje istotną przewagę nad oszacowanym przez Baltara czasem 61 lat.

Oczywiście, rzeczywistość może postawić nam dodatkowe wymagania, nawet jeśli założymy, że Baltar jest geniuszem, jego urządzenie nigdy nie zawodzi i nie ma potrzeby powtórnego testowania próbek na obecność błędów. Po pierwsze - wykresy powyższe zostały utworzone przy założeniu istnienia siedmiu Cylonów we flocie. W istocie ta liczba nie była znana z góry, więc oszacowanie optymalnej wielkości grup testowych może być dość trudne. Po drugie - wyznaczona matematycznie optymalna wielkość grupy może być niepraktyczna w zastosowaniu. Na przykład "ślady cyloństwa" pojedynczej osoby w grupie wielkości 4080 (optymalnej dla metody połowienia) mogą być tak rozcieńczone, że praktycznie niewykrywalne przez aparaturę. Czytelnika zainteresowanego dokładnymi rozważaniami na te tematy, jak również analizą błędów pomiaru oraz możliwego odchylenia liczby testów od wartości oczekiwanej, odsyłam do oryginalnej pracy Ch.R. Bildera, gdzie te zagadnienia są poruszane.

Nam wystarczy informacja, że gdyby Baltar zastosował nawet najbardziej naiwną metodę testowania grupowego (Dorfmana), nawet dla mocno nieoptymalnej wielkości grup równej 16, to badania zajęłyby mu co najwyżej 4 lata - a więc skończyłby je wystarczająco wcześnie, by miało to wpływ na fabułę. Jako że wśród cylońskich agentów były osoby kluczowe dla bezpieczeństwa floty, ich wykrycie mogłoby mieć daleko idące konsekwencje, przede wszystkim dla widzów: spadek napięcia wywołanego paranoją i zapewne związany z tym spadek zainteresowania serialem. Może więc tym razem niekonsultowanie badań ze statystykiem wyszło wszystkim na dobre?