Podstawową jednostką funkcjonalną każdej sztucznej sieci neuronowej jest sztuczny neuron. Dlatego przed stworzeniem takiej sieci należy dysponować matematycznym modelem pojedynczej komórki nerwowej. Taki model jest najprostszym do analizy elementem sieci neuronowej i poznanie go może stanowić wstęp do rozważań na temat sztucznych sieci neuronowych.

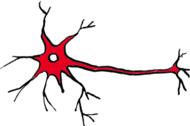
Standardowa komórka nerwowa składa się z ciała komórki (perikarionu) oraz odchodzących od niego elementów - pojedynczego aksonu (neurytu) i wielu dendrytów. Neurony pełnią funkcję odbierania, przekazywania, przetwarzania i gromadzenia informacji. Komórki nerwowe są ułożone w sieć i komunikują się ze sobą. Aktywność tych komórek manifestuje się zmianami napięcia w obrębie ich błony komórkowej. W stanie spoczynku neurony wykazują stałą różnicę potencjału elektrycznego pomiędzy wnętrzem komórki a środowiskiem zewnętrznym, której wartość wynosi średnio 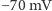. W naturze sygnały docierające do neuronów powodują zmiany napięcia błony komórkowej. Gdy wartość tych bodźców jest odpowiednio wysoka, aby spowodować wzrost potencjału błonowego do progowej wartości 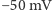, obserwuje się aktywację komórki. Następuje wtedy kaskada procesów fizjologicznych w obrębie błony komórkowej, co jest widoczne jako nagły wzrost potencjału elektrycznego, sięgającego dodatnich wartości (patrz rysunek). Droga wygenerowanego sygnału biegnie wzdłuż aksonu, który następnie łączy się z wieloma dendrytami kolejnych neuronów. Po przekazaniu informacji komórka stabilizuje różnicę potencjału elektrycznego do wartości spoczynkowej i jest gotowa na odbieranie kolejnych bodźców. Wzorując się na naturze, sztuczny neuron powinien więc odbierać wiele sygnałów wejściowych (dendryty) z różnych źródeł i generować jeden sygnał wyjściowy (akson).

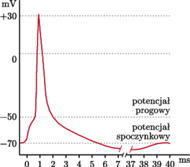
Wartość potencjału elektrycznego pobudzonego neuronu

W naturalnej sieci neuronowej informacje docierające do komórek nerwowych mają różne wartości. Od ich sumy zależy, czy docelowy neuron zostanie pobudzony, a co za tym idzie, czy sygnał zostanie przekazany dalej, czy ulegnie wygaśnięciu. Pobudzenie komórki nerwowej jest zgodne z zasadą "wszystko albo nic". Mówi ona o tym, że neuron zostanie pobudzony tylko wtedy, gdy suma wartości sygnałów docierających jest większa lub równa wartości progowej 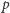pobudzającej komórkę. Mniejsze wartości nie są w stanie wywołać żadnej odpowiedzi ze strony komórki docelowej. Taką właściwość neuronów niezwykle łatwo przenieść na grunt cyfrowy i przedstawić za pomocą systemu binarnego, gdzie cyfra 1 oznaczać będzie pobudzenie komórki, a 0 - stan spoczynku.

Istotne jest, że sygnały odbierane przez komórki mogą być nasilane lub wyciszane. Pozwala to na zaistnienie sytuacji, w której pewne informacje są faworyzowane, co odbywa się poprzez wzrost wartości z podprogowej na pobudzającą. W odwrotnym przypadku informacja progowa może zostać uznana za nieistotną i przestać generować pobudzenia. Przypisywanie wag poszczególnym sygnałom odbieranym pozwala sieciom neuronowym uczyć się i samodoskonalić. Taka umiejętność jest bardzo praktyczna dla naukowców, ponieważ modele komputerowe, które uczą się na własnych błędach, nie wymagają wprowadzania tak wielu poprawek, jak modele bez tej zdolności. W naturze selekcja bodźców zewnętrznych odbywa się przez skomplikowane mechanizmy biochemiczne. Aktywność neuronów jest regulowana między innymi przez uwalnianie związków chemicznych, które ułatwiają lub hamują pobudzenie. Żywe komórki nerwowe mają zdolność kategoryzowania sygnałów, ponieważ uczenie się i dostosowywanie do zmiennego otoczenia jest cechą korzystną ewolucyjnie.

Inaczej jest w sztucznych sieciach neuronowych, w których powyższe właściwości komórek zostały zastąpione opisem matematycznym. Sztuczne neurony, pracujące nad rozwiązaniem danego problemu, rozpoczynają obliczenia, wykorzystując wartości sygnałów wejściowych oraz wybranych losowo wag. Po uzyskaniu wyniku, a z nim wielkości funkcji błędu, sieć neuronowa poszukuje takich wartości wag, dla których błąd ten jest najmniejszy. Następnie obliczenia są przeprowadzane tak długo, aż uzyskana zostanie zadowalająco mała wartość błędu. Decyzje, jak zmieniać wartości wag, sztuczna sieć neuronowa podejmuje na podstawie odpowiednich algorytmów. Jest ich wiele rodzajów i wiele modyfikacji, a o ich wyborze decyduje badacz podczas tworzenia sieci.

Sztuczne sieci neuronowe znajdują ogromne zastosowanie w wielu obszarach nauki oraz życia codziennego. Wykorzystuje się je w różnych, niejednokrotnie odległych aspektach ludzkiej działalności, jak, na przykład, finanse, medycyna. Sztuczne sieci neuronowe potrafią analizować odręcznie pismo chińskie, czuwać nad bezpieczeństwem pracy robotów czy sterować transportem w firmach przewozowych. Programy komputerowe bazujące na modelach neuronów są często stosowane do badań określanych mianem in silico. W wielu laboratoriach przed przystąpieniem do doświadczeń empirycznych stosuje się wstępne analizy z użyciem modelowania komputerowego. Takie postępowanie jest korzystne dla badaczy, ponieważ pozwala na wstępne odrzucenie tych obiektów badań, które już na tym etapie nie wykazały obiecujących właściwości. To z kolei przekłada się na skrócenie czasu i zmniejszenie kosztów eksperymentu.

Znana każdemu użytkownikowi Internetu firma Google także wykorzystuje sztuczne sieci neuronowe. Przykładem może być model, pracujący na specjalnie dla niego zbudowanym sprzęcie elektronicznym, składającym się z 16 tysięcy procesorów. Umożliwiło to stworzenie sztucznej sieci zawierającej trzy miliony neuronów i miliard połączeń. Po zleceniu sieci neuronowej analizy filmów z serwisu YouTube okazało się, że oprogramowanie to samodzielnie nauczyło się wyróżniać pewne obiekty, jak na przykład ludzkie twarze czy wizerunki kotów. Ze względu na fakt, że badane przez sieć neuronową filmy były pozbawione jakichkolwiek opisów kategoryzujących, można wnioskować, że model neuronowy wykreował na własne potrzeby koncepcje przedstawianych obiektów i na tej podstawie zaczął je wyróżniać. Można to porównać do sytuacji, w której człowiek obserwuje obcy gatunek zwierzęcia i uczy się jego zachowania. Zastosowanie sztucznych sieci neuronowych przez Google prawdopodobnie nie skończy się na powyższym przykładzie. Dalszy rozwój takich modeli może umożliwić doskonalenie poszczególnych usług internetowych. Na przykład samouczące się oprogramowanie mogłoby ulepszyć algorytmy popularnego obecnie tłumacza Google, co skutkowałoby trafnymi tłumaczeniami w zależności od użytego kontekstu. Dodatkowo opracowanie doskonalszego programu do rozpoznawania mowy zaowocowałoby dokładną analizą wypowiadanych słów i ich natychmiastowym tłumaczeniem, bez konieczności używania klawiatury. Być może w niedalekiej przyszłości każdy korzystający z wyszukiwarki internetowej będzie miał kontakt z wynikami opracowanymi przez sztuczną sieć neuronową.

Pomimo wielu zalet modelowanie wzorowane na neuronach nigdy nie daje gwarancji powodzenia i tak jak każda metoda eksperymentalna niesie za sobą więcej porażek niż sukcesów. Mnogość badań pomyślnie wykorzystujących sztuczne sieci neuronowe wynika nie tyle z ich niezawodności, co z ogromnego obszaru ich zastosowań. Warto także zwrócić uwagę na fakt, że w świecie naukowym rzadko publikowane są wyniki nieudanych eksperymentów.

W przypadku próby opisu obiektu za pomocą modelu matematycznego należy też pamiętać, że w rzeczywistości modelowaniu nie podlega sam obiekt, a jedynie nasza wiedza o nim. Dlatego im mniej mamy informacji na temat danego zjawiska, tym gorszy otrzymamy model. Zestawiając zachowanie modelu z rzeczywistym zachowaniem przedmiotu badań, po pewnym czasie (na ogół) obserwuje się rozbieżności pomiędzy tymi dwoma procesami. Wynika to właśnie z niepełnej wiedzy badacza na temat modelowanego zjawiska. Ze względu na niezwykle wysoki poziom skomplikowania procesów naturalnych modelowanie pozwala na oszacowanie wyników zawsze obarczonych pewnym błędem. Możliwości sztucznych sieci neuronowych są także zależne od wykorzystywanego sprzętu komputerowego. Jest tak, ponieważ ze wzrostem liczby modelowanych parametrów rośnie zapotrzebowanie na moc obliczeniową.