O spinach i genach
Czego można się nauczyć, studiując na Wydziale Matematyki, Informatyki i Mechaniki UW?
Odpowiedź krótka: wszystkiego tego, co można sformułować precyzyjnie w języku matematyki, czyli wszystkiego.
Odpowiedź praktyczna: tego, czym się zajmują nasi pracownicy - kilka przykładów przedstawimy w tym i następnych artykułach.
Odpowiedź konkretna: na przykład, zachowania się układów wielu oddziałujących obiektów. Ja zajmuję się tym przez całe życie, ciągle tym samym, a jednak za każdym razem czymś innym. Na początku były to oddziałujące atomy oraz cząsteczki tworzące kryształy i inne ciała stałe, potem nastał czas graczy (czasami nazywanych agentami) - czyli ludzi lub zwierząt - w teorii gier ewolucyjnych, a teraz są to głównie białka w matematycznych modelach regulacji genów.
Każdy z tych obiektów oddziałuje z innymi obiektami znajdującymi się w pewnym sąsiedztwie. Zachowanie danego obiektu zależy od jego położenia, prędkości i innych charakterystyk, zwanych stanami tej cząstki lub osobnika, ale też od stanu obiektów, z którymi oddziałuje. Ruch oddziałujących cząstek opisują równania Newtona - równania różniczkowe II zasady dynamiki znane Wam z liceum (zapewne byliście nieświadomi, że spotkaliście już wtedy na swojej drodze równania różniczkowe). Przypomnijmy: zmiana stanu danego obiektu zależy od jego stanu i od stanów wszystkich obiektów, z którymi oddziałuje, a zmiana ich stanów zależy od stanu danego obiektu itd., itd. W tym momencie być może niektórym z Was przypominają się wypowiedzi Russella Crowe'a, czyli Johna Nasha z filmu Piękny umysł. Jak chcecie się dowiedzieć, czym różnią się równowagi Nasha oddziałujących graczy od stanów równowagowych oddziałujących cząstek w fizyce statystycznej, to przyjdźcie na nasz wydział, niecierpliwym polecam notatki do wykładu Modele matematyki stosowanej [1].
W układach bardzo wielu oddziałujących obiektów niemożliwe jest śledzenie każdego z nich, niemożliwe jest analityczne rozwiązanie odpowiednich równań, a nawet gdybyśmy rozwiązali je numerycznie, to bylibyśmy przytłoczeni kosmiczną ilością danych liczbowych. Naszym celem może być obliczenie średniego zachowania, czyli - jak to mówią matematycy - wartości oczekiwanej. I to, niestety, też jest trudne zadanie.
Nadszedł czas, aby przedstawić głównego aktora naszej opowieści - pole średnie. Otóż niezwykle prosty pomysł polega na tym, aby oddziaływanie danego obiektu z innymi obiektami przedstawić jako oddziaływanie danego obiektu z (nieznanym) średnim otoczeniem wytworzonym przez pozostałe obiekty. Powtórzmy: otrzymany w ten sposób układ to jeden obiekt oddziałujący z uśrednionym otoczeniem. W tak prostym układzie względnie łatwo jest obliczyć jego średni stan. Otrzymany wzór zawiera nieznane pole średnie, a więc jest de facto równaniem na nieznaną wartość pola średniego. Możemy rozwiązać to równanie, czyli - jak mówią fizycy - samouzgodnić pole średnie, które musi być równe średniemu stanowi naszego wyjściowego obiektu.
Proste, nieprawdaż? Ale, jak powszechnie wiadomo, diabeł tkwi w konkretnych przykładach. Zobaczymy, że nie taki on straszny.
Przykład 1: Dlaczego istnieje magnes?
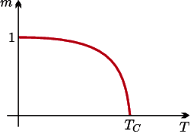
Rys. 1 Namagnesowanie jako funkcja temperatury
Fizycy wiedzą, że podgrzany magnes traci swoje własności magnetyczne. Zjawisko to stara się wyjaśnić teoria ciała stałego, dział fizyki zajmujący się własnościami ciał makroskopowych. W bardzo dużym uproszczeniu przyjmujemy, że namagnesowanie ciała jest sumą wektorową małych magnesów związanych z jego poszczególnymi atomami. Z jednej strony, siły oddziaływań pomiędzy magnesikami prowadzą do ich ułożenia wzdłuż jednego kierunku. Sąsiednie magnesiki lubią układać się w tym samym kierunku (wtedy mają najmniejszą energię i tak - od sąsiada do sąsiada - ta chęć naśladowania trafia do wszystkich). Z drugiej strony, ruchy cieplne atomów zaburzają ten idealny porządek. Wynikiem tych dwóch przeciwstawnych oddziaływań jest ustalenie się równowagowego namagnesowania ciała. Wynikałoby z tego, że namagnesowanie jest malejącą funkcją temperatury, zbiegającą do zera wraz z jej wzrostem. Okazuje się jednak, jak to widzimy na rysunku 1, że istnieje temperatura krytyczna, tak zwana temperatura Curie, powyżej której ciało całkowicie traci własności magnetyczne - mamy do czynienia z przejściem fazowym. Nasze pierwsze ćwiczenie w używaniu pola średniego pozwoli nam wyjaśnić to niezwykle ciekawe i nieintuicyjne zjawisko.
Magnes matematyczny - ferromagnetyczny model Isinga
W modelu Isinga oddziałujące obiekty - magnesiki - umieszczone są w węzłach regularnej kraty sześciennej 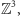 gdzie
gdzie 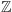 jest zbiorem liczb całkowitych. W każdym węźle
jest zbiorem liczb całkowitych. W każdym węźle 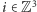 umieszczamy matematyczną reprezentację
umieszczamy matematyczną reprezentację 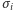 magnesiku, zmienną mogącą przyjmować dwie wartości:
magnesiku, zmienną mogącą przyjmować dwie wartości: 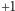 (magnesik skierowany do góry) i
(magnesik skierowany do góry) i 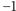 (magnesik skierowany do dołu). Zmienną
(magnesik skierowany do dołu). Zmienną 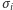 nazywamy spinem w węźle
nazywamy spinem w węźle 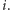 Niech
Niech 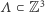 będzie skończonym podzbiorem węzłów naszej kraty.
będzie skończonym podzbiorem węzłów naszej kraty. 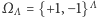 jest zbiorem konfiguracji na
jest zbiorem konfiguracji na 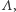 czyli zbiorem wszystkich funkcji przypisujących węzłom spin skierowany do góry lub do dołu. A teraz najważniejsza rzecz: jak oddziałują ze sobą spiny. O tym mówi hamiltonian, czyli funkcja na
czyli zbiorem wszystkich funkcji przypisujących węzłom spin skierowany do góry lub do dołu. A teraz najważniejsza rzecz: jak oddziałują ze sobą spiny. O tym mówi hamiltonian, czyli funkcja na 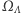 przypisująca energię konfiguracjom na
przypisująca energię konfiguracjom na 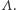 Przyjmujemy, że oddziałują ze sobą spiny, które są najbliższymi sąsiadami,
Przyjmujemy, że oddziałują ze sobą spiny, które są najbliższymi sąsiadami,

gdzie 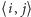 jest parą najbliższych sąsiadów, a
jest parą najbliższych sąsiadów, a 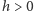 jest zewnętrznym polem magnetycznym.
jest zewnętrznym polem magnetycznym.
Hamiltonian w mechanice klasycznej oddziałujących cząstek jest sumą ich energii kinetycznych i energii potencjalnej oddziaływań między nimi. W powyższym wyrażeniu nie uwzględniamy energii kinetycznej.
Nasz układ spinowy podlega nieustannym ruchom cieplnym i w związku z tym nawet w równowadze jest układem stochastycznym. Powinniśmy więc określić prawdopodobieństwa przebywania układu w każdym z mikroskopowych stanów, czyli elementów zbioru 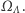 Wszelkie makroskopowe wielkości fizyczne, takie jak energia czy namagnesowanie układu, są więc zmiennymi losowymi na
Wszelkie makroskopowe wielkości fizyczne, takie jak energia czy namagnesowanie układu, są więc zmiennymi losowymi na 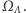 Interesować nas będą wartości oczekiwane tych zmiennych losowych. Wprowadzamy następujący rozkład prawdopodobieństwa,
Interesować nas będą wartości oczekiwane tych zmiennych losowych. Wprowadzamy następujący rozkład prawdopodobieństwa,

gdzie 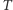 jest temperaturą układu, czyli miarą jego ruchów cieplnych, a
jest temperaturą układu, czyli miarą jego ruchów cieplnych, a
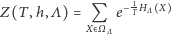
jest czynnikiem normalizującym prawdopodobieństwo. W fizyce 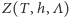 nazywane jest sumą statystyczną, natomiast
nazywane jest sumą statystyczną, natomiast 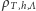 - wielkim rozkładem kanonicznym albo stanem Gibbsa. Ciekawy świata Czytelnik może znaleźć uzasadnienie wprowadzenia takiego, a nie innego rozkładu prawdopodobieństwa we wspomnianych już notatkach.
- wielkim rozkładem kanonicznym albo stanem Gibbsa. Ciekawy świata Czytelnik może znaleźć uzasadnienie wprowadzenia takiego, a nie innego rozkładu prawdopodobieństwa we wspomnianych już notatkach.

Definiujemy teraz zmienną losową namagnesowania układu:

Aby uniknąć niepotrzebnych, drugorzędnych problemów technicznych, wprowadzamy periodyczne warunki brzegowe, a więc zwijamy 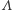 w trójwymiarowy torus. Na wartość oczekiwaną
w trójwymiarowy torus. Na wartość oczekiwaną 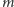 zmiennej losowej
zmiennej losowej 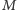 w stanie Gibbsa otrzymujemy wtedy wyrażenie
w stanie Gibbsa otrzymujemy wtedy wyrażenie

gdzie 0 jest dowolnym węzłem, 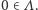
Występowanie w sumie 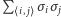 iloczynów
iloczynów 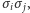 a więc oddziaływań między spinami, nie pozwala znaleźć wzoru na
a więc oddziaływań między spinami, nie pozwala znaleźć wzoru na  Na pomoc przychodzi pole średnie. Zmieniamy
Na pomoc przychodzi pole średnie. Zmieniamy 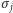 w powyższych iloczynach na (nieznaną) wartość oczekiwaną
w powyższych iloczynach na (nieznaną) wartość oczekiwaną 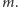 Każdy spin oddziałuje z sześcioma sąsiednimi spinami, co oznacza, że zastępujemy
Każdy spin oddziałuje z sześcioma sąsiednimi spinami, co oznacza, że zastępujemy 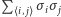 przez
przez 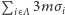 (uwaga: aby nie uwzględniać dwa razy oddziaływania pomiędzy spinami w węzłach
(uwaga: aby nie uwzględniać dwa razy oddziaływania pomiędzy spinami w węzłach 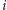 i
i 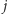 piszemy
piszemy 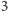 zamiast
zamiast 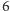 ). Czytelnik łatwo zauważy, że zarówno licznik, jak i mianownik można przedstawić za pomocą odpowiednich iloczynów, i po prostych przekształceniach otrzyma równanie
). Czytelnik łatwo zauważy, że zarówno licznik, jak i mianownik można przedstawić za pomocą odpowiednich iloczynów, i po prostych przekształceniach otrzyma równanie

gdzie 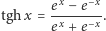 Zauważmy, że zewnętrzne pole magnetyczne
Zauważmy, że zewnętrzne pole magnetyczne 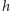 zostało zmodyfikowane przez średnie pole
zostało zmodyfikowane przez średnie pole 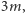 które interpretujemy jako efektywne pole pochodzące z uśrednienia oddziaływań danego spinu. Jesteśmy w szczególny sposób zainteresowani przypadkiem zerowego pola zewnętrznego,
które interpretujemy jako efektywne pole pochodzące z uśrednienia oddziaływań danego spinu. Jesteśmy w szczególny sposób zainteresowani przypadkiem zerowego pola zewnętrznego, 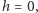 to znaczy namagnesowaniem spontanicznym. Aby dostać w takim przypadku samouzgodnioną wartość
to znaczy namagnesowaniem spontanicznym. Aby dostać w takim przypadku samouzgodnioną wartość 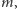 musimy rozwiązać równanie
musimy rozwiązać równanie
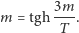 |
(1) |
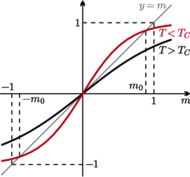
Rys. 2 Graficzne rozwiązanie równania pola średniego (1).
Możemy je rozwiązać graficznie. Znajdujemy przecięcie wykresu funkcji 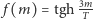 i linii prostej
i linii prostej 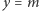 (patrz rysunek 2). Łatwo zauważyć, że dla
(patrz rysunek 2). Łatwo zauważyć, że dla 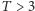 oba wykresy przecinają się tylko w jednym punkcie
oba wykresy przecinają się tylko w jednym punkcie 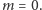 Jeśli jednak
Jeśli jednak 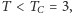 wykresy przecinają się w trzech punktach i w ten sposób dostajemy trzy rozwiązania:
wykresy przecinają się w trzech punktach i w ten sposób dostajemy trzy rozwiązania: 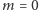 i
i 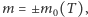 gdzie
gdzie 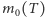 jest dodatnim namagnesowaniem.
jest dodatnim namagnesowaniem. 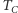 jest krytyczną temperaturą Curie, w której zachodzi przejście fazowe. Rysunek 1 to wniosek z rysunku 2; nasz cel został osiągnięty.
jest krytyczną temperaturą Curie, w której zachodzi przejście fazowe. Rysunek 1 to wniosek z rysunku 2; nasz cel został osiągnięty.
Można udowodnić, że dla 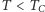 rozwiązanie
rozwiązanie 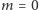 jest termodynamicznie niestabilne. Współistnienie dwóch rozwiązań
jest termodynamicznie niestabilne. Współistnienie dwóch rozwiązań 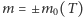 jest wynikiem symetrii hamiltonianu (w przypadku zerowego pola zewnętrznego,
jest wynikiem symetrii hamiltonianu (w przypadku zerowego pola zewnętrznego, 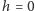 ) ze względu na odwrócenie spinów
) ze względu na odwrócenie spinów 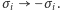 Oznacza to, że w temperaturze niższej od krytycznej współistnieją dwa makroskopowe stany równowagowe naszego magnesu.
Oznacza to, że w temperaturze niższej od krytycznej współistnieją dwa makroskopowe stany równowagowe naszego magnesu.
Przykład 2: Samoograniczający się gen
Produkcja białek w komórkach jest wynikiem różnych biochemicznych procesów. Umożliwiają one różnicowanie się komórek i ich odpowiedź na zmieniające się środowisko. O tym, jakie białko powstanie, decyduje informacja genetyczna zapisana w DNA. W najprostszym modelu produkcji białka, czyli - jak to mówią biolodzy - ekspresji genu, w każdym momencie może zajść jedno z dwóch zdarzeń: produkcja lub degradacja jednej cząsteczki białka. Opisujemy to matematycznie stochastycznymi procesami urodzin i śmierci. W procesie takim stan komórki w każdej chwili jest określony przez liczbę cząsteczek białka. Zmiany stanu w czasie zachodzą z odpowiednimi prawdopodobieństwami. Zakładamy, że jeśli w czasie 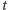 w komórce było
w komórce było 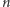 cząsteczek białka, to
cząsteczek białka, to
- Prawdopodobieństwo produkcji (urodzin) jednej cząsteczki w odcinku czasowym
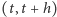 wynosi
wynosi 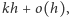
- Prawdopodobieństwo degradacji (śmierci) jednej cząsteczki w odcinku czasowym
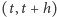 wynosi
wynosi 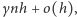
- Prawdopodobieństwo wystąpienia więcej niż jednej zmiany (reakcji) w odcinku czasowym
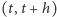 wynosi
wynosi 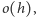
gdzie 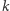 i
i 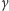 to intensywności produkcji i degradacji, a
to intensywności produkcji i degradacji, a 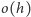 jest wielkością mniejszego rzędu niż
jest wielkością mniejszego rzędu niż 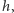 to znaczy
to znaczy 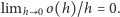
Oznaczmy przez 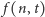 prawdopodobieństwo tego, że w komórce w chwili
prawdopodobieństwo tego, że w komórce w chwili 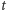 jest
jest  cząsteczek białka. Naszym celem jest znalezienie wzoru na wartość stacjonarną, czyli niezależną od czasu
cząsteczek białka. Naszym celem jest znalezienie wzoru na wartość stacjonarną, czyli niezależną od czasu 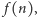 albo przynajmniej na wartość średnią liczby cząsteczek białka,
albo przynajmniej na wartość średnią liczby cząsteczek białka, 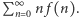 Aby coś obliczyć, trzeba na to coś ułożyć równanie i, oczywiście, potem je rozwiązać. By w komórce było
Aby coś obliczyć, trzeba na to coś ułożyć równanie i, oczywiście, potem je rozwiązać. By w komórce było  cząsteczek w chwili
cząsteczek w chwili 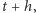 powinno być
powinno być 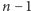 cząsteczek w chwili
cząsteczek w chwili 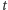 i jedna cząsteczka powinna być wyprodukowana w czasie
i jedna cząsteczka powinna być wyprodukowana w czasie 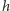 lub
lub 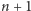 cząsteczek w chwili
cząsteczek w chwili 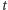 i jedna cząsteczka powinna zdegradować w czasie
i jedna cząsteczka powinna zdegradować w czasie 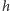 lub
lub  cząsteczek w chwili
cząsteczek w chwili 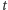 i nic nie powinno się zdarzyć w czasie
i nic nie powinno się zdarzyć w czasie 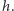
Możemy napisać wyrażenie na prawdopodobieństwo całkowite:

Przenosimy teraz 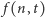 na lewą stronę, dzielimy przez
na lewą stronę, dzielimy przez 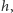 przechodzimy do granicy
przechodzimy do granicy 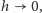 dostajemy pochodną jako granicę ilorazu różnicowego, czyli po prostu prędkość zmian prawdopodobieństwa, i ostatecznie otrzymujemy nieskończony układ równań różniczkowych zwyczajnych:
dostajemy pochodną jako granicę ilorazu różnicowego, czyli po prostu prędkość zmian prawdopodobieństwa, i ostatecznie otrzymujemy nieskończony układ równań różniczkowych zwyczajnych:
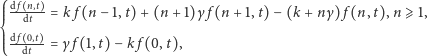 |
(2) |
powiedzmy, z warunkiem początkowym 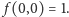 Jest to słynne równanie M.
Jest to słynne równanie M.
Nie będziemy go rozwiązywać. Interesować nas będzie stan stacjonarny 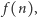 w którym wpływy i wypływy w księgowaniu prawdopodobieństw równoważą się. Funkcja
w którym wpływy i wypływy w księgowaniu prawdopodobieństw równoważą się. Funkcja 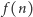 jest rozwiązaniem nieskończonego układu równań algebraicznych, opisujących równowagę globalną, uzyskanych z (2) przez przyrównanie do zera pochodnych czasowych.
jest rozwiązaniem nieskończonego układu równań algebraicznych, opisujących równowagę globalną, uzyskanych z (2) przez przyrównanie do zera pochodnych czasowych.
Rozwiążemy powyższy układ równań krok po kroku. Z równania na 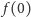 dostajemy
dostajemy 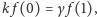 z równania na
z równania na 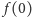 i uwzględnieniu poprzedniej relacji dostajemy
i uwzględnieniu poprzedniej relacji dostajemy 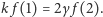 Czytelniku, proszę, sprawdź, że dla dowolnego
Czytelniku, proszę, sprawdź, że dla dowolnego 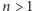 mamy
mamy 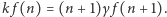 Łatwo zrozumieć, dlaczego relacje takie nazywamy warunkami równowagi szczegółowej. Teraz już szybko zdążamy do mety, czyli do wzoru na rozkład prawdopodobieństwa
Łatwo zrozumieć, dlaczego relacje takie nazywamy warunkami równowagi szczegółowej. Teraz już szybko zdążamy do mety, czyli do wzoru na rozkład prawdopodobieństwa 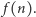 Wyznaczamy kolejno z powyższych wzorów
Wyznaczamy kolejno z powyższych wzorów 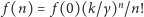 i po uwzględnieniu warunku, że suma wszystkich prawdopodobieństw musi być równa 1, otrzymujemy
i po uwzględnieniu warunku, że suma wszystkich prawdopodobieństw musi być równa 1, otrzymujemy

Jest to słynny rozkład Poissona.
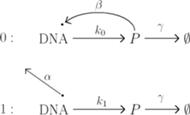
Rys. 3 Samoograniczający się gen, 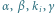 są odpowiednio intensywnościami odłączania i przyłączania białka do promotora, produkcji i degradacji białka.
są odpowiednio intensywnościami odłączania i przyłączania białka do promotora, produkcji i degradacji białka.
Ale życie, czyli biologia, nie jest takie proste. Okazuje się, że bardzo często gen sam siebie ogranicza. Dzieje się to w ten sposób, że cząsteczka białka może związać się z pewną częścią DNA zwaną promotorem i ograniczyć jego ekspresję, czyli produkcję następnych cząsteczek. W modelu matematycznym przyjmujemy, że DNA może znajdować się w dwóch stanach: stanie związanym, oznaczanym przez 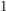 i w stanie wolnym
i w stanie wolnym 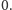 W stanie wolnym produkcja białka zachodzi z intensywnością
W stanie wolnym produkcja białka zachodzi z intensywnością 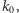 a w stanie związanym - z intensywnością
a w stanie związanym - z intensywnością 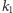 (rysunek 3).
(rysunek 3).
Stan naszej komórki jest teraz dodatkowo opisany przez 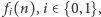 i jest łącznym prawdopodobieństwem tego, że w komórce w chwili
i jest łącznym prawdopodobieństwem tego, że w komórce w chwili 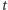 jest
jest 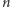 cząsteczek białka, a DNA jest w stanie
cząsteczek białka, a DNA jest w stanie 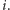 Wtedy dla
Wtedy dla 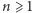 równanie M ma następującą postać:
równanie M ma następującą postać:

gdzie 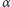 jest intensywnością odłączania białka od promotora, a
jest intensywnością odłączania białka od promotora, a 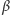 intensywnością przyłączania. Zauważmy, że zgodnie z obserwacjami biologicznymi związana cząsteczka białka nie ulega degradacji.
intensywnością przyłączania. Zauważmy, że zgodnie z obserwacjami biologicznymi związana cząsteczka białka nie ulega degradacji.

Okazuje się, że powyższego układu równań nie możemy rozwiązać nawet w stanie stacjonarnym. Łatwo sprawdzić, że nie są spełnione warunki równowagi szczegółowej. I znowu na pomoc przychodzi pole średnie. Zastępujemy 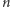 w składnikach opisujących przełączanie się genu między dwoma stanami przez jego nieznaną wartość oczekiwaną.
w składnikach opisujących przełączanie się genu między dwoma stanami przez jego nieznaną wartość oczekiwaną.
Niestety, nadal nie umiemy rozwiązać równania M w stanie stacjonarnym (brak równowagi szczegółowej nadal nam doskwiera), ale przynajmniej dostajemy - tak jak w modelu Isinga - równanie (dokładniej: układ równań) na nieznaną wartość oczekiwaną. Rozwiązujemy równania i dostajemy wzór na wartość oczekiwaną liczby cząsteczek białka w stanie stacjonarnym, a to zawsze cieszy matematyków i mamy nadzieję, że również będzie cieszyć biologów. Kończy nam się czas i przestrzeń przeznaczona na rozważania o polu średnim dla samoograniczającego się genu, zaciekawionych Czytelników odsyłamy znowu do naszych notatek i do artykułu naukowego [1, 2], a także do [3].
O innych ciekawych zastosowaniach matematyki można przeczytać w artykułach Marka Bodnara, Urszuli Foryś i Pawła Matejka w sierpniowym numerze Delty w 2014 roku oraz Witolda Sadowskiego w numerze grudniowym. I oczywiście przeczytajcie w tym numerze artykuł Tadeusza Płatkowskiego o dylematach społecznych, Wojciecha Niemiry o spacerach i polimerach oraz Piotra Dittwalda o (nie)prawdopodobnych izotopach. I do zobaczenia na Banacha (wejście od Pasteura).
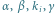 są odpowiednio intensywnościami odłączania i przyłączania białka do promotora, produkcji i degradacji białka.
są odpowiednio intensywnościami odłączania i przyłączania białka do promotora, produkcji i degradacji białka.