Demokracja i (NP-)trudne problemy
Podczas XXVII Kongresu Matematycznego, odbywającego się w Seulu między 13 a 21 sierpnia 2014 roku, prestiżową Nagrodę Nevanlinny (informatyczny odpowiednik Medalu Fieldsa) otrzymał pracujący w USA hinduski informatyk Subhash Khot. W laudacji poświęconej wynikom Khota jego mentor i współautor wielu prac, Sanjeev Arora, wspomniał o przełomowym wyniku uzyskanym przez profesora Uniwersytetu Warszawskiego, Krzysztofa Oleszkiewicza wraz z Elchananem Mosselem i Ryanem O'Donnellem...
W pracy Noise stability of functions with low influences: Invariance and optimality, opublikowanej w Annals of Mathematics w 2010 roku, udowodniona została, istotnie związana z wynikami Subhasha Khota, hipoteza Większość jest najbardziej stabilna (MiS, Majority is Stablest). Hipotezę tę można interpretować w języku teorii zajmującej się systemami głosowania. Fascynujące jest jej powiązanie z należącymi do informatyki teoretycznej wynikami Khota, które z kolei są ściśle związane z nierozstrzygniętą hipotezą 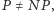 wartego milion dolarów Problemu Milenijnego. Została ona postawiona na początku lat 70. niezależnie przez Stephena Cooka i Leonida Levina. Mimo upływu przeszło 40 lat nikomu nie udało się ani jej udowodnić, ani obalić. Jak każdy wielki problem, stała się źródłem wielu cennych wyników w różnych działach matematyki i informatyki teoretycznej, szczególnie w teorii złożoności obliczeniowej.
wartego milion dolarów Problemu Milenijnego. Została ona postawiona na początku lat 70. niezależnie przez Stephena Cooka i Leonida Levina. Mimo upływu przeszło 40 lat nikomu nie udało się ani jej udowodnić, ani obalić. Jak każdy wielki problem, stała się źródłem wielu cennych wyników w różnych działach matematyki i informatyki teoretycznej, szczególnie w teorii złożoności obliczeniowej.
Problem 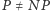 jest związany z konstrukcją efektywnych, czyli wykonywanych w realistycznym czasie, algorytmów. Czas wykonywania algorytmu zależy od wielkości użytych w nim danych. Mówimy, że jest on wielomianowy, jeśli istnieją takie stałe
jest związany z konstrukcją efektywnych, czyli wykonywanych w realistycznym czasie, algorytmów. Czas wykonywania algorytmu zależy od wielkości użytych w nim danych. Mówimy, że jest on wielomianowy, jeśli istnieją takie stałe 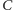 i
i 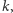 że dla danych o rozmiarze
że dla danych o rozmiarze  algorytm potrzebuje co najwyżej
algorytm potrzebuje co najwyżej 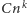 kroków. Klasę problemów, dla których istnieje algorytm rozwiązania w wielomianowym czasie, oznaczamy przez
kroków. Klasę problemów, dla których istnieje algorytm rozwiązania w wielomianowym czasie, oznaczamy przez 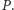 Istnieją problemy, o których nie wiadomo, czy należą do tej klasy, można jednak w czasie wielomianowym sprawdzić poprawność dowolnie zadanego rozwiązania. O takich problemach mówimy, że należą do klasy
Istnieją problemy, o których nie wiadomo, czy należą do tej klasy, można jednak w czasie wielomianowym sprawdzić poprawność dowolnie zadanego rozwiązania. O takich problemach mówimy, że należą do klasy 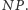 Oczywiście, gdy problem jest klasy
Oczywiście, gdy problem jest klasy 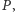 to jest również klasy
to jest również klasy 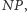 gdyż w takim przypadku możemy sprawdzić poprawność rozwiązania w czasie wielomianowym, po prostu sami je rozwiązując. Czy prawdziwe jest twierdzenie odwrotne, oznaczające, że każdy problem, którego rozwiązanie można efektywnie sprawdzić, ma efektywny algorytm jego rozwiązania? Gdyby umiejętność oceny poprawności rozwiązania pociągała zdolność do jego konstrukcji, czyli gdyby
gdyż w takim przypadku możemy sprawdzić poprawność rozwiązania w czasie wielomianowym, po prostu sami je rozwiązując. Czy prawdziwe jest twierdzenie odwrotne, oznaczające, że każdy problem, którego rozwiązanie można efektywnie sprawdzić, ma efektywny algorytm jego rozwiązania? Gdyby umiejętność oceny poprawności rozwiązania pociągała zdolność do jego konstrukcji, czyli gdyby 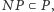 to, jak powiedział profesor MIT Scott Aaronson, każdy, kto umiałby docenić piękno symfonii, zostałby Mozartem. Każdy, kto potrafi śledzić rozumowanie krok po kroku, zostałby Gaussem.
to, jak powiedział profesor MIT Scott Aaronson, każdy, kto umiałby docenić piękno symfonii, zostałby Mozartem. Każdy, kto potrafi śledzić rozumowanie krok po kroku, zostałby Gaussem.
Przykładem zagadnienia ściśle powiązanego z tą problematyką jest próba znalezienia minimalnego pokrycia grafu niezorientowanego. W roku 1972 Richard M. Karp z Uniwersytetu Kalifornijskiego w Berkeley wykazał, że jeśli 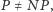 to nie istnieje efektywny (czyli działający w wielomianowym czasie) sposób rozwiązania tego zadania. Rozważmy jednak następujący, prosty algorytm:
to nie istnieje efektywny (czyli działający w wielomianowym czasie) sposób rozwiązania tego zadania. Rozważmy jednak następujący, prosty algorytm:
- 1.
- Wybierz krawędź grafu. Dołącz do pokrycia oba wierzchołki połączone tą krawędzią.
- 2.
- suń z grafu te wierzchołki i wszystkie krawędzie zawierające co najmniej jeden z tych wierzchołków.
- 3.
- Powtarzaj kroki 1-2 aż do wyczerpania krawędzi grafu.
Nietrudno zauważyć, że ten algorytm znajduje pokrycie grafu. Nie musi być ono minimalne, zawiera jednak co najwyżej dwukrotnie więcej wierzchołków niż rozwiązanie idealne (wśród każdej pary usuwanych wierzchołków musi znaleźć się co najmniej jeden należący do pokrycia minimalnego). Skonstruowaliśmy zatem przykład algorytmu przybliżonego ze współczynnikiem 2. Ogólniej:
Algorytm rozwiązania problemu minimum jest przybliżony ze współczynnikiem
jeśli znalezione za jego pomocą rozwiązanie
spełnia dla każdej instancji warunek
gdzie
jest minimalizowaną funkcją, a
rozwiązaniem optymalnym.
Analogicznie możemy zdefiniować przybliżony algorytm rozwiązania problemu maksimum ze współczynnikiem 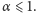 Takie rozwiązania mają wielkie znaczenie praktyczne - skoro nie można osiągnąć efektywnego rozwiązania optymalnego, sięga się po prostsze rozwiązania przybliżone. Powstaje naturalne pytanie, czy aktualnie funkcjonujące rozwiązania można jeszcze choć trochę polepszyć, a więc dla jakich
Takie rozwiązania mają wielkie znaczenie praktyczne - skoro nie można osiągnąć efektywnego rozwiązania optymalnego, sięga się po prostsze rozwiązania przybliżone. Powstaje naturalne pytanie, czy aktualnie funkcjonujące rozwiązania można jeszcze choć trochę polepszyć, a więc dla jakich 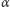 istnieją przybliżone rozwiązania efektywne o tym współczynniku. Okazuje się, że istnienie takich granic efektywności również związane jest z omawianą hipotezą. W roku 2002 Irit Dinur i Shmuel Safra pokazali, że jeśli
istnieją przybliżone rozwiązania efektywne o tym współczynniku. Okazuje się, że istnienie takich granic efektywności również związane jest z omawianą hipotezą. W roku 2002 Irit Dinur i Shmuel Safra pokazali, że jeśli 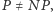 to dla problemu minimalnego pokrycia grafu nie istnieje nawet przybliżony algorytm o wielomianowym czasie działania o współczynniku mniejszym niż
to dla problemu minimalnego pokrycia grafu nie istnieje nawet przybliżony algorytm o wielomianowym czasie działania o współczynniku mniejszym niż 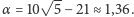
W roku 2001 pojawił się inny ciekawy problem optymalizacyjny, który przedstawił swojemu promotorowi, Sanjeevowi Arorze, 23-letni student Uniwersytetu Princeton, Subhash Khot. Zadanie jest wariantem problemu kolorowania wierzchołków grafu na 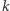 kolorów w taki sposób, aby wierzchołki połączone krawędzią miały różne kolory. Istnieje prosty i efektywny algorytm rozstrzygający, czy pokolorowanie jest możliwe dla
kolorów w taki sposób, aby wierzchołki połączone krawędzią miały różne kolory. Istnieje prosty i efektywny algorytm rozstrzygający, czy pokolorowanie jest możliwe dla 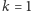 i
i 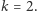 Dla
Dla 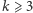 jest to problem
jest to problem 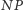 -trudny, czyli problem, do którego można w czasie wielomianowym przekształcić każdy problem
-trudny, czyli problem, do którego można w czasie wielomianowym przekształcić każdy problem 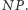 Oznacza to, że gdy
Oznacza to, że gdy 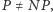 to nie istnieje efektywny algorytm kolorowania.
to nie istnieje efektywny algorytm kolorowania.
To, co odróżnia przypadek 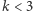 od przypadku
od przypadku 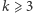 i co jest jednym z powodów tak nagłego wzrostu złożoności, to fakt, że w tym drugim przypadku kolor wierzchołka nie wyznacza jednoznacznie koloru jego sąsiadów. Khot zaproponował, by dla każdej krawędzi wyznaczony był zestaw dopuszczalnych pokolorowań końców, zwanych ograniczeniami, w którym kolor jednego końca krawędzi jednoznacznie wyznacza kolor drugiego. Czasami taki zestaw ograniczeń jest sprzeczny - nie istnieje pokolorowanie grafu spełniające wszystkie ograniczenia. I tu Khot zażądał, aby znaleźć pokolorowanie spełniające maksymalną liczbę ograniczeń. Innymi słowy, dla każdego grafu z ograniczeniami poszukuje się pokolorowania o maksymalnej wartości, czyli ułamka liczby krawędzi grafu, spełniających przypisane im ograniczenia. Ta maksymalna wartość wynosi 1 w grafie, dla którego istnieje pokolorowanie spełniające wszystkie ograniczenia, jeśli natomiast nie istnieje pokolorowanie spełniające którekolwiek z ograniczeń, wynosi 0. Maksymalna wartość w grafie z drugiego przykładu wynosi
i co jest jednym z powodów tak nagłego wzrostu złożoności, to fakt, że w tym drugim przypadku kolor wierzchołka nie wyznacza jednoznacznie koloru jego sąsiadów. Khot zaproponował, by dla każdej krawędzi wyznaczony był zestaw dopuszczalnych pokolorowań końców, zwanych ograniczeniami, w którym kolor jednego końca krawędzi jednoznacznie wyznacza kolor drugiego. Czasami taki zestaw ograniczeń jest sprzeczny - nie istnieje pokolorowanie grafu spełniające wszystkie ograniczenia. I tu Khot zażądał, aby znaleźć pokolorowanie spełniające maksymalną liczbę ograniczeń. Innymi słowy, dla każdego grafu z ograniczeniami poszukuje się pokolorowania o maksymalnej wartości, czyli ułamka liczby krawędzi grafu, spełniających przypisane im ograniczenia. Ta maksymalna wartość wynosi 1 w grafie, dla którego istnieje pokolorowanie spełniające wszystkie ograniczenia, jeśli natomiast nie istnieje pokolorowanie spełniające którekolwiek z ograniczeń, wynosi 0. Maksymalna wartość w grafie z drugiego przykładu wynosi 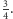
Gdy maksymalna wartość grafu jest równa 1, to szybko można znaleźć właściwe pokolorowanie. Wystarczy rozpatrzeć wszystkie przypadki pokolorowania jednego węzła, gdyż determinują one jednoznacznie pokolorowanie całego grafu. Takie grafy łatwo rozpoznać, jest to jednak znacznie trudniejsze dla grafów z maksymalną wartością nawet nieznacznie mniejszą od 1. Okazuje się bowiem, że odróżnienie dwóch skrajnych typów grafów:
- graf, dla którego najlepsze pokolorowanie ma wartość co najmniej równą
 dla danego z góry
dla danego z góry 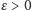 (przypadek TAK),
(przypadek TAK), - graf, dla którego najlepsze pokolorowanie ma wartość co najwyżej równą
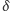 dla danego z góry
dla danego z góry 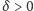 (przypadek NIE),
(przypadek NIE),
jest bardzo problematyczne, jeśli dysponujemy dużą liczbą kolorów (i tym samym dużą liczbą ograniczeń dla krawędzi). Trudność tę formalnie wyraża sformułowana przez Khota w 2002 roku hipoteza Unique Games Conjecture 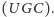
Dla każdej pary
istnieje taka liczba kolorów
że odróżnienie grafu spełniającego przypadek TAK od grafu spełniającego przypadek NIE jest
-trudne.
Hipoteza 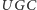 do dziś nie została rozstrzygnięta. Jej istnienie pozwala jednak spojrzeć na znane problemy z nowego punktu widzenia. Gdyby była prawdziwa, to znalezienie nawet przybliżonego rozwiązania dla wielu problemów okazałoby się niezwykle trudne. Wiemy już, na przykład, że w problemie minimalnego pokrycia grafu nie ma nawet przybliżonego efektywnego rozwiązania o współczynniku mniejszym niż
do dziś nie została rozstrzygnięta. Jej istnienie pozwala jednak spojrzeć na znane problemy z nowego punktu widzenia. Gdyby była prawdziwa, to znalezienie nawet przybliżonego rozwiązania dla wielu problemów okazałoby się niezwykle trudne. Wiemy już, na przykład, że w problemie minimalnego pokrycia grafu nie ma nawet przybliżonego efektywnego rozwiązania o współczynniku mniejszym niż 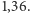 Znamy za to proste rozwiązanie o współczynniku 2.
Znamy za to proste rozwiązanie o współczynniku 2.
W 2003 roku Khot i Regev wykazali, że
gdy hipoteza
jest prawdziwa, to znalezienie przybliżonego rozwiązania o dowolnym współczynniku mniejszym od 2 jest
-trudne.
Oznacza to, że zaproponowane przez nas proste rozwiązanie przybliżone jest najlepszym nietrudnym sposobem podejścia do zadania.
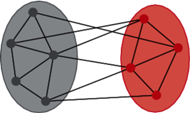
Rozmiar cięcia jest równy 6.
Kolejnym znanym problemem jest znalezienie maksymalnego cięcia w grafie (problem 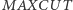 ). Polega on na podziale wierzchołków grafu na dwa podzbiory (tzn. dokonaniu cięcia). Jego rozmiarem nazwiemy liczbę krawędzi "granicznych", których wierzchołki należą do różnych podzbiorów. Należy oczywiście znaleźć cięcie o największym rozmiarze.
). Polega on na podziale wierzchołków grafu na dwa podzbiory (tzn. dokonaniu cięcia). Jego rozmiarem nazwiemy liczbę krawędzi "granicznych", których wierzchołki należą do różnych podzbiorów. Należy oczywiście znaleźć cięcie o największym rozmiarze. 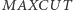 jest problemem
jest problemem 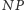 -trudnym, a więc (o ile
-trudnym, a więc (o ile 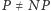 ) nie istnieje efektywny sposób znalezienia maksymalnego cięcia. Sensownym rozwiązaniem jest znalezienie algorytmu przybliżonego. Pierwszy algorytm o współczynniku
) nie istnieje efektywny sposób znalezienia maksymalnego cięcia. Sensownym rozwiązaniem jest znalezienie algorytmu przybliżonego. Pierwszy algorytm o współczynniku 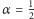 znaleziono w roku 1976. Po 18 latach Goemans i Williamson znaleźli lepszy algorytm, oparty na rozumowaniu czysto geometrycznym, co wprawiło w zdumienie znawców zagadnienia. Wyznaczony przez nich współczynnik
znaleziono w roku 1976. Po 18 latach Goemans i Williamson znaleźli lepszy algorytm, oparty na rozumowaniu czysto geometrycznym, co wprawiło w zdumienie znawców zagadnienia. Wyznaczony przez nich współczynnik 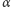 wynosi
wynosi

Podobnie, jak w przypadku minimalnego pokrycia grafu, hipoteza 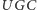 wyjaśnia sprawę do końca, to znaczy
wyjaśnia sprawę do końca, to znaczy
Jeżeli hipoteza
jest prawdziwa, to każdy przybliżony algorytm w problemie
o współczynniku większym niż
jest
-trudny.
Rezultat ten został opublikowany w 2005 roku, ale przy dodatkowym założeniu o prawdziwości wówczas jeszcze nierozstrzygniętej hipotezy MiS. Dowód jej prawdziwości ogłoszono jednak jeszcze w tym samym roku w materiałach pewnej konferencji poświęconej podstawom informatyki - jednym ze współautorów tego wyniku jest wspomniany już Krzysztof Oleszkiewicz. Najlepsze przybliżone rozwiązanie problemu 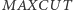 zależy więc tylko od prawdziwości hipotezy
zależy więc tylko od prawdziwości hipotezy 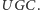
Przyjrzyjmy się bliżej hipotezie MiS. Jest ona związana z analizą harmoniczną funkcji boolowskich. Definicje i twierdzenia w tej dziedzinie zazwyczaj formułowane są w języku polityki i teorii wyboru socjalnego (np. współczynnik siły koalicji Banzhafa czy twierdzenie Arrowa o dyktaturze). Hipoteza dotyczy stabilności systemu głosowania, w którym głosuje się na jedną z alternatyw, tak jak w wyborach prezydenckich w Stanach Zjednoczonych. System wyborów w tym kraju jest pośredni: wyborcy głosują na kolegium elektorskie, a następnie elektorzy dokonują wyboru prezydenta. W wielu krajach panuje bezpośredni system większościowy, gdzie większość głosów wyborców decyduje o wyborze.
Spektakularnym przykładem występowania niestabilności systemu elektorskiego był przypadek wyborów prezydenckich w roku 2000. Rywalizowali wtedy George W. Bush i Al Gore. Języczkiem u wagi w tych wyborach okazało się głosowanie na Florydzie. Wyniki we wszystkich stanach, bez Florydy, wskazywały na wygraną Busha w większości stanów, ale Gore miał więcej głosów elektorskich. Różnica głosów na Florydzie była niewielka, a co więcej, niestarannie przygotowana karta do głosowania mogła spowodować błędne zakwalifikowanie głosu przez maszynę zliczającą. Walka toczyła się o decydujące 25 głosów elektorskich Florydy. Ostatecznie Bush otrzymał na Florydzie 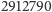 głosów, Al Gore
głosów, Al Gore 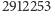 głosy. Przewaga Busha wyniosła tylko 537 głosów (przewaga
głosy. Przewaga Busha wyniosła tylko 537 głosów (przewaga 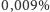 ). Gdyby w Stanach Zjednoczonych panował system większościowy bezpośredni, wybory wygrałby Gore. W obowiązującym systemie elektorskim wygrał jednak Bush.
). Gdyby w Stanach Zjednoczonych panował system większościowy bezpośredni, wybory wygrałby Gore. W obowiązującym systemie elektorskim wygrał jednak Bush.
Niestabilność systemu objawiła się zbytnią wrażliwością systemu elektorskiego na niepewne wyniki u niewielkiej liczby głosujących. W tym przypadku wady tej nie miał system bezpośredni. Spróbujmy ją opisać za pomocą matematycznego formalizmu. Niech 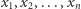 będą wynikami głosowania na jednego z dwóch kandydatów, które koduje się jako
będą wynikami głosowania na jednego z dwóch kandydatów, które koduje się jako 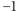 i 1. System głosowania jest funkcją
i 1. System głosowania jest funkcją 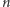 zmiennych
zmiennych 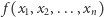 o wartościach w zbiorze
o wartościach w zbiorze 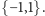 System, w którym istnieje taki wskaźnik
System, w którym istnieje taki wskaźnik 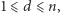 że
że 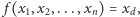 nazywa się dyktaturą, a wyborca o indeksie
nazywa się dyktaturą, a wyborca o indeksie 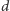 - dyktatorem. System opisany funkcją
- dyktatorem. System opisany funkcją

nazywany jest większościowym. Wpływem 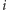 -tego wyborcy na wynik głosowania jest liczba
-tego wyborcy na wynik głosowania jest liczba

gdzie 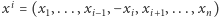 jest głosowaniem, w którym
jest głosowaniem, w którym 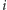 -ty wyborca zmienił swoją decyzję. Wpływ
-ty wyborca zmienił swoją decyzję. Wpływ 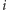 -tego wyborcy jest zatem prawdopodobieństwem zauważenia skutku zmiany decyzji tego wyborcy. Dla dyktatury
-tego wyborcy jest zatem prawdopodobieństwem zauważenia skutku zmiany decyzji tego wyborcy. Dla dyktatury 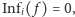 gdy
gdy 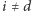 oraz
oraz 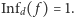 Dyktator ma absolutny wpływ na wynik wyborów, inni wyborcy nie mają żadnego. System uważa się za daleki od dyktatury, gdy dla pewnego małego
Dyktator ma absolutny wpływ na wynik wyborów, inni wyborcy nie mają żadnego. System uważa się za daleki od dyktatury, gdy dla pewnego małego 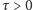 zachodzi
zachodzi 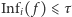 dla każdego wyborcy
dla każdego wyborcy 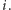 O liczbie
O liczbie  można zatem myśleć jako o poziomie niezależności od dyktatury. Dla systemu większościowego
można zatem myśleć jako o poziomie niezależności od dyktatury. Dla systemu większościowego

Wpływ każdego z wyborców jest taki sam i jest niewielki, gdy liczba wyborców jest duża - przy takiej liczbie wyborców system większościowy jest zatem daleki od dyktatury.

Badanie jakości systemu głosowania prowadzi się poprzez analizę jego własności w najbardziej nieprzewidywalnych warunkach, to znaczy wtedy, gdy wyborcy głosują niezależnie i z tym samym prawdopodobieństwem na każdego z kandydatów. Jeśli wówczas 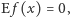 to mówimy, że system wyborczy jest zrównoważony. Aby zbadać jego podatność na zmiany, rozważymy sytuację, w której każdy z wyborców zmienił decyzję z ustalonym prawdopodobieństwem. Niech zatem
to mówimy, że system wyborczy jest zrównoważony. Aby zbadać jego podatność na zmiany, rozważymy sytuację, w której każdy z wyborców zmienił decyzję z ustalonym prawdopodobieństwem. Niech zatem 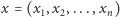 będzie wektorem wyników głosowania oraz niech
będzie wektorem wyników głosowania oraz niech 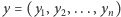 będzie wektorem, jaki powstałby z wektora
będzie wektorem, jaki powstałby z wektora 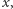 gdyby każdy z wyborców losowo i z prawdopodobieństwem
gdyby każdy z wyborców losowo i z prawdopodobieństwem 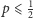 zmienił swoją decyzję. Wtedy
zmienił swoją decyzję. Wtedy 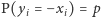 i
i 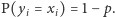 Wektory
Wektory 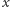 i
i 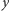 są ze sobą ściśle związane. Ich współczynnik korelacji wynosi
są ze sobą ściśle związane. Ich współczynnik korelacji wynosi 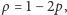 jest nieujemny i jest malejącą funkcją
jest nieujemny i jest malejącą funkcją 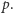 Funkcjonał
Funkcjonał

nazywa się stabilnością na poziomie 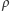 systemu
systemu 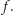 Wartości
Wartości 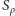 zbliżone do zera charakteryzują systemy stabilne. Dla dyktatury
zbliżone do zera charakteryzują systemy stabilne. Dla dyktatury 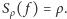 Dla systemu większościowego stabilność jest skomplikowaną funkcją
Dla systemu większościowego stabilność jest skomplikowaną funkcją 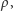 można jednak obliczyć granicę
można jednak obliczyć granicę

Teraz wreszcie można sformułować hipotezę MiS.
Zadane są: współczynnik korelacji
i mała liczba
Istnieje wtedy takie
że dla wszystkich zrównoważonych systemów wyborczych o poziomie niezależności od dyktatury
zachodzi
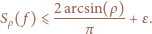
Hipoteza została udowodniona we wspomnianej pracy Mossela, O'Donnella i Oleszkiewicza. W tej samej pracy została udowodniona jeszcze jedna niezwykle interesująca hipoteza, występująca pod barokową nazwą It Ain't Over Till It's Over. Mówi ona, że dla zrównoważonych systemów wyborczych istnieje taki poziom niezależności od dyktatury, że nawet gdy ujawni się frakcję 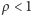 głosów losowo wybranych wyborców, to niezależnie od wartości
głosów losowo wybranych wyborców, to niezależnie od wartości 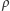 z dużym prawdopodobieństwem wynik wyborów jest jeszcze niezdecydowany. W systemach dalekich od dyktatury ujawnienie nawet dużej frakcji wyników wyborów jeszcze nie daje pewności co do ostatecznego rezultatu. Boleśnie przekonał się o tym Al Gore i zapewne niewielkim pocieszeniem byłaby dla niego świadomość, z jak doniosłym matematycznym problemem związana była jego porażka w walce o prezydencki fotel.
z dużym prawdopodobieństwem wynik wyborów jest jeszcze niezdecydowany. W systemach dalekich od dyktatury ujawnienie nawet dużej frakcji wyników wyborów jeszcze nie daje pewności co do ostatecznego rezultatu. Boleśnie przekonał się o tym Al Gore i zapewne niewielkim pocieszeniem byłaby dla niego świadomość, z jak doniosłym matematycznym problemem związana była jego porażka w walce o prezydencki fotel.
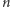 nieparzystego, co w praktyce nie jest żadnym ograniczeniem.
nieparzystego, co w praktyce nie jest żadnym ograniczeniem.