W krainie średnich
Zdarza się czasami, że kiedy po przeprowadzeniu doświadczenia analizujemy dane, niektóre liczby wyglądają dziwnie - to znaczy inaczej, niż byśmy się spodziewali. W statystyce takie obserwacje, które są zdecydowanie większe lub zdecydowanie mniejsze od ogółu obserwacji nazywa się obserwacjami odstającymi (ang. outliers).
Bardzo często pojawiają się one w próbie w wyniku błędów popełnionych w trakcie dokonywania obserwacji lub podczas późniejszego przetwarzania danych, na przykład przy wpisywaniu danych (przykładowo, wpisanie liczby 98 bądź 0,98 zamiast 9,8). Obecność takich błędnych wartości w próbce może wpływać niekorzystnie na wyniki obliczeń. W tym miejscu nasuwa się pytanie, czy nie należałoby usuwać ze zbioru danych "podejrzanych" wyników. Jeśli jesteśmy przekonani, że mamy faktycznie do czynienia z błędem, możemy to uczynić. Jednakże nie należy tego czynić pochopnie, bowiem obserwacje odstające nie zawsze są efektami błędów. Czasem są to wartości jak najbardziej prawidłowe, tyle że pojawiające się w danym doświadczeniu stosunkowo rzadko.
Mamy, na szczęście, do dyspozycji kilka prostych narzędzi statystycznych pozwalających poradzić sobie ze zniekształcaniem wyników pomiarów przez obserwacje odstające. Dla 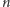 -elementowego ciągu obserwacji
-elementowego ciągu obserwacji 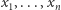 możemy obliczyć średnią ważoną, zdefiniowaną wzorem
możemy obliczyć średnią ważoną, zdefiniowaną wzorem
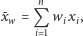 |
(1) |
gdzie ciąg nieujemnych wag 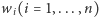 spełnia
spełnia 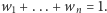 Średnie ważone mogą różnić się nie tylko wartościami wag, ale i sposobem, w jaki wagi przypisywane są obserwacjom. W tradycyjnej średniej ważonej (1)
Średnie ważone mogą różnić się nie tylko wartościami wag, ale i sposobem, w jaki wagi przypisywane są obserwacjom. W tradycyjnej średniej ważonej (1) 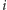 -ta waga
-ta waga 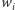 mnożona jest przez
mnożona jest przez 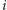 -tą obserwację
-tą obserwację 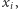 bez względu na to, jaką wartość przyjmuje
bez względu na to, jaką wartość przyjmuje 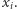 W wielu sytuacjach wielce użyteczne bywają jednak takie średnie, dla których przydział wag jest uzależniony od uporządkowania obserwacji.
W wielu sytuacjach wielce użyteczne bywają jednak takie średnie, dla których przydział wag jest uzależniony od uporządkowania obserwacji.
Uporządkowaną średnią ważoną, czyli w skrócie OWA (ang. Ordered Weighted Average), nazywamy średnią, w której 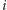 -ta waga
-ta waga 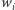 mnożona jest przez
mnożona jest przez 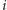 -tą co do wielkości obserwację
-tą co do wielkości obserwację 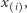 co możemy zapisać jako
co możemy zapisać jako
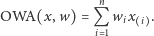 |
(2) |
W statystyce wyrażenie (2) bywa nazywane L-statystyką. Szczególnym przypadkiem OWA jest tzw. średnia ucięta, której krańcowe pod względem wielkości obserwacje otrzymują wagę równą zeru. Średnią uciętą definiujemy więc jako
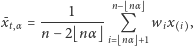 |
(3) |
gdzie 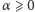 jest tzw. wskaźnikiem ucięcia. Aby wzór (3) miał sens, wskaźnik ucięcia nie może być zbyt duży, a konkretnie, musi spełniać ograniczenie
jest tzw. wskaźnikiem ucięcia. Aby wzór (3) miał sens, wskaźnik ucięcia nie może być zbyt duży, a konkretnie, musi spełniać ograniczenie 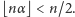 Indeks
Indeks 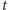 występujący w symbolu średniej uciętej (2) pochodzi od angielskiej nazwy tej średniej, trimmed mean. To właśnie średnią uciętą stosuje się w praktyce po to, by wyeliminować wpływ ekstremalnych obserwacji.
występujący w symbolu średniej uciętej (2) pochodzi od angielskiej nazwy tej średniej, trimmed mean. To właśnie średnią uciętą stosuje się w praktyce po to, by wyeliminować wpływ ekstremalnych obserwacji.
W tym kontekście średnia ucięta może być postrzegana jako narzędzie pozwalające wyznaczyć przeciętną wartość badanej cechy w taki sposób, by nie tracąc z oczu obserwacji odstających, ignorować ich wpływ na dokonywane obliczenia. O średniej uciętej mówi się, iż jest ona odporna na obecność obserwacji odstających w próbce. Tej własności nie ma natomiast zwykła średnia arytmetyczna, która przykłada taką samą wagę do wszystkich obserwacji, w tym także odstających.
Ilustracją stosowania średniej uciętej w życiu codziennym może być sposób oceny skoczków narciarskich. Jak wiadomo, skok oceniany jest przez pięciu sędziów, przy czym faktyczna ocena skoku dokonywana jest na podstawie trzech ocen pozostałych po wyeliminowaniu dwóch ocen ekstremalnych - minimalnej i maksymalnej. Celem takiego postępowania jest uniknięcie sytuacji, w której sędzia miałby faworyzować skoczka wystawiając mu notę dużo wyższą niż pozostali sędziowie, bądź też chciałby ocenić skok dużo gorzej niż inni jurorzy.
Dopuszczając maksymalny stopień ucięcia otrzymujemy średnią uciętą postaci
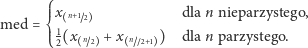 |
(4) |
Ten szczególny przypadek średniej uciętej nazywamy medianą.
Mediana w sposób oczywisty jest odporna na wartość obserwacji odstających, bowiem, jak widać ze wzoru (4), bazuje wyłącznie na obserwacjach położonych w samym środku uporządkowanej niemalejąco próbki. W pewnych sytuacjach bywa to zaletą, ale trzeba pamiętać, że stosując zbyt duże ucięcie pozbywamy się nie tylko obserwacji odstających, ale i wielu cennych informacji zawartych w próbce. Tak więc w przypadku średniej uciętej, podobnie jak w życiu codziennym, trzeba postępować rozważnie i nie popadać w skrajności.
Jeszcze innym rodzajem średniej, używanej w statystyce i odpornej na obecność obserwacji odstających, jest tzw. średnia winsorowska. Wyznacza się ją w sposób podobny do średniej uciętej, tyle że zamiast eliminowania krańcowych obserwacji z uporządkowanego ciągu, zastępuje się je odpowiednio dobranymi wartościami. Dokładniej, po uporządkowaniu zbioru obserwacji w sposób niemalejący, ucinamy ustaloną liczbę krańcowych obserwacji (od dołu i od góry), a następnie dopisujemy tyle obserwacji, ile łącznie ucięliśmy, przy czym połowa spośród dopisanych obserwacji ma być równa pierwszej, a połowa ostatniej obserwacji z podzbioru, który pozostał po ucięciu. W przypadku średniej winsorowskiej, w przeciwieństwie do średniej uciętej, mamy do czynienia nie tyle z eliminacją obserwacji odstających, co raczej z ograniczeniem ich wpływu na wyznaczaną wartość przeciętną.

Przykładowe 11 wartości wyników pomiarów oraz ich średnia arytmetyczna (A), mediana (M) i średnia ucięta z parametrem ucięcia 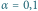 (U). Zestaw danych na rysunku po prawej stronie różni się od tego po lewej tym, że wartość pomiaru zaznaczonego pustym kółkiem została (przypadkowo?) zmniejszona dziesięciokrotnie.
(U). Zestaw danych na rysunku po prawej stronie różni się od tego po lewej tym, że wartość pomiaru zaznaczonego pustym kółkiem została (przypadkowo?) zmniejszona dziesięciokrotnie.
Jak widać, pojęcie wartości przeciętnej, czy też średniej, mimo iż tak intuicyjne, niekoniecznie musi prowadzić do średniej arytmetycznej. Jakkolwiek jest ona powszechnie i często z powodzeniem stosowana w praktyce, zdarzają się i takie sytuacje, w których jej użycie może przynieść niepożądane efekty. Pamiętajmy, że w wielu sytuacjach dobór właściwej średniej może się okazać decydujący dla poprawności uzyskiwanych wniosków.
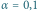 (U). Zestaw danych na rysunku po prawej stronie różni się od tego po lewej tym, że wartość pomiaru zaznaczonego pustym kółkiem została (przypadkowo?) zmniejszona dziesięciokrotnie.
(U). Zestaw danych na rysunku po prawej stronie różni się od tego po lewej tym, że wartość pomiaru zaznaczonego pustym kółkiem została (przypadkowo?) zmniejszona dziesięciokrotnie.