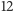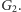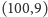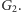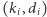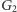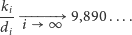O modelowaniu przydziału częstotliwości za pomocą kolorowania grafów
Teoria grafów to gałąź matematyki, do której powstania impuls dało liczące sobie już ćwierć tysiąclecia słynne zagadnienie mostów królewieckich, rozwiązane przez Leonharda Eulera. Osobiście lubię patrzeć na matematykę nie tylko jako na zbiór problemów ciekawych samych w sobie, ale również jak na model rzeczywistości, narzędzie pozwalające efektywniej radzić sobie z rzeczywistymi zmartwieniami. Obecnie teoria grafów staje się jednym z najpopularniejszych takich narzędzi, używanym chętnie przez matematyków (na rzecz innych gałęzi tej nauki), informatyków, fizyków, chemików, a nawet socjologów. Niniejszy artykuł ma na celu przedstawienie tego, jak zagadnienie kolorowania grafów służyć może za narzędzie przydatne w przydzielaniu częstotliwości nadajnikom w jednym z modeli sieci radiowej.
Problem nadajników
Nasze rozważania zaczniemy od rzeczywistego zagadnienia. Wyobraźmy sobie, że mamy sieć nadajników/odbiorników radiowych (telefonii komórkowej) - każdy nadajnik ma ograniczony zasięg bezpośredniej komunikacji z innymi nadajnikami. Urządzenia nadające na tej samej częstotliwości mają to do siebie, że mogą się wzajemnie zagłuszać, interferować - tzn. jeśli pewien nadajnik "słyszy" jednocześnie sygnały z dwóch innych, to tak naprawdę nic "nie słyszy". Zakładamy, że stacje znajdujące się w swoim zasięgu (czyli mogące "rozmawiać" bezpośrednio między sobą) szybko uzgodnią nadawanie i nie będą jednocześnie wysyłać wiadomości do wspólnego sąsiada. Problem pozostaje z takimi stacjami, które nie mogą się komunikować bezpośrednio (są poza swoim zasięgiem), ale mają inną stację w swoim wspólnym zasięgu - a zatem mogą się czasem zagłuszać.
Jak można zapobiec zagłuszaniu w takich przypadkach? Możemy przydzielić każdej stacji pewien odcinek czasu (tzw. szczelinę czasową) w taki sposób, aby nadajniki potencjalnie konfliktowe otrzymały rozłączne odcinki czasu. Ale jak to zrobić? Z pomocą przyjdzie nam teoria grafów!
Klasyczne i ułamkowe kolorowanie grafów
Przypomnijmy, że grafem nazywamy parę 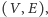 gdzie
gdzie 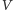 to zbiór wierzchołków, a
to zbiór wierzchołków, a 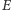 to pewien zbiór par wierzchołków z
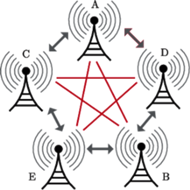
to pewien zbiór par wierzchołków z 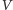 nazywanych krawędziami. W naturalny sposób przedstawimy konflikty w naszej sieci w postaci grafu: wierzchołki będą odpowiadać nadajnikom, a krawędziami połączymy te nadajniki, które mogą się zagłuszać, tzn. te, które są poza swoim zasięgiem, ale mają inny nadajnik w swoim wspólnym zasięgu. Obok mamy przykład tworzenia grafu konfliktów pewnej sieci - kolorowe linie oznaczają konflikt, czyli krawędź w grafie.
nazywanych krawędziami. W naturalny sposób przedstawimy konflikty w naszej sieci w postaci grafu: wierzchołki będą odpowiadać nadajnikom, a krawędziami połączymy te nadajniki, które mogą się zagłuszać, tzn. te, które są poza swoim zasięgiem, ale mają inny nadajnik w swoim wspólnym zasięgu. Obok mamy przykład tworzenia grafu konfliktów pewnej sieci - kolorowe linie oznaczają konflikt, czyli krawędź w grafie.
Przyjmijmy w tworzonym modelu, że wszystkie nadajniki są równie ważne, tzn. w ramach cyklu pracy każda stacja ma otrzymać pewną jednostkę czasu dostępnego do nadawania. Nasze pierwsze podejście będzie następujące: jeden cykl nadawania będzie składał się z 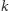 ponumerowanych liczbami
ponumerowanych liczbami 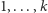 odcinków czasu jednostkowej długości i będziemy starali się tak przydzielić wierzchołkom liczby, aby wierzchołki połączone krawędzią (sąsiedzi w grafie) otrzymały różne odcinki czasu. Im mniejsze
odcinków czasu jednostkowej długości i będziemy starali się tak przydzielić wierzchołkom liczby, aby wierzchołki połączone krawędzią (sąsiedzi w grafie) otrzymały różne odcinki czasu. Im mniejsze 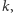 dla którego uda się to zrealizować, tym lepiej - cykl nadawania będzie krótszy przy tej samej skuteczności. To, co właśnie opisaliśmy, to tak naprawdę klasyczne zagadnienie kolorowania grafu:
dla którego uda się to zrealizować, tym lepiej - cykl nadawania będzie krótszy przy tej samej skuteczności. To, co właśnie opisaliśmy, to tak naprawdę klasyczne zagadnienie kolorowania grafu:
Definicja. 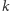 -kolorowaniem grafu
-kolorowaniem grafu 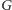 nazywamy takie przyporządkowanie wierzchołkom kolorów spośród
nazywamy takie przyporządkowanie wierzchołkom kolorów spośród 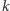 kolorów, że każde wierzchołki połączone krawędzią mają różne kolory. Liczbę chromatyczną
kolorów, że każde wierzchołki połączone krawędzią mają różne kolory. Liczbę chromatyczną 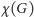 definiujemy jako minimalne
definiujemy jako minimalne 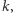 dla którego istnieje
dla którego istnieje 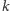 -kolorowanie grafu
-kolorowanie grafu 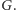
Zatem w naszym podejściu najlepszy przydział szczelin czasowych odpowiada kolorowaniu grafu 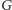 sieci na
sieci na 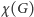 kolorów.
kolorów.
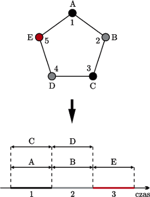
Przykład schematu nadawania długości 3
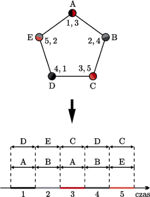
Przykład schematu nadawania długości 2,5 - wyraźna oszczędność
A gdybyśmy podzielili odcinki czasu przydzielane nadajnikom na mniejsze kawałki, powiedzmy długości 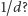 Nadal wymagamy, aby w jednym cyklu pracy każdy nadajnik otrzymał sumarycznie jedną jednostkę czasu, ale tym razem podzielmy cały cykl pracy (ponownie
Nadal wymagamy, aby w jednym cyklu pracy każdy nadajnik otrzymał sumarycznie jedną jednostkę czasu, ale tym razem podzielmy cały cykl pracy (ponownie 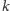 odcinków) na odcinki długości
odcinków) na odcinki długości 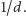 Z tego wynika, że każdy nadajnik powinien otrzymać
Z tego wynika, że każdy nadajnik powinien otrzymać 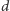 odcinków, czyli
odcinków, czyli 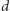 różnych liczb - sprowadza się to do tzw. ułamkowego kolorowania grafów:
różnych liczb - sprowadza się to do tzw. ułamkowego kolorowania grafów:
Definicja. 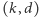 -kolorowaniem grafu
-kolorowaniem grafu 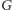 nazywamy takie przyporządkowanie wierzchołkom
nazywamy takie przyporządkowanie wierzchołkom 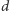 -elementowych zbiorów kolorów spośród
-elementowych zbiorów kolorów spośród 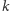 kolorów, że każde wierzchołki połączone krawędzią otrzymują rozłączne zbiory. Ułamkową liczbę chromatyczną
kolorów, że każde wierzchołki połączone krawędzią otrzymują rozłączne zbiory. Ułamkową liczbę chromatyczną 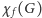 grafu
grafu 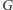 definiujemy jako kres dolny liczb
definiujemy jako kres dolny liczb 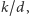 dla których istnieje
dla których istnieje 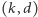 -kolorowanie grafu
-kolorowanie grafu 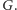
Warto zwrócić uwagę na fakt, że ułamkowa liczba chromatyczna danego grafu jest zawsze nie większa niż liczba chromatyczna - wynika to z faktu, że 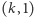 -kolorowanie jest tym samym co
-kolorowanie jest tym samym co 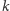 -kolorowanie. Oznacza to, że podejście ułamkowe może dać tylko oszczędność w stosunku do klasycznego kolorowania!
-kolorowanie. Oznacza to, że podejście ułamkowe może dać tylko oszczędność w stosunku do klasycznego kolorowania!
Podkreślmy, że ułamek 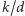 odpowiada długości jednego cyklu pracy, przy cały czas ustalonej skuteczności jednego cyklu. A zatem dążymy do cyklu pracy długości
odpowiada długości jednego cyklu pracy, przy cały czas ustalonej skuteczności jednego cyklu. A zatem dążymy do cyklu pracy długości 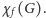
Jak znaleźć przydział czasów?
Jak więc możemy znaleźć konkretny schemat nadawania? Niestety, sprawa nie jest łatwa.
Wydaje się, że mogą być dwa podejścia:
- I
- Obliczeniowe: stosowanie algorytmów kolorowania do konkretnych sieci/grafów;
- II
- Uniwersalne: użycie narzędzi teoretycznych do uzyskania uniwersalnych rozwiązań.
W przypadku I problem polega na tym, że nie znamy szybkich algorytmów kolorowania grafów - zarówno w przypadku klasycznego kolorowania, jak i w ułamkowej wersji. Oznacza to, że dla małych grafów znajdziemy optymalne rozwiązanie, ale w przypadku większych grafów optymalne rozwiązanie ( 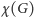 bądź
bądź 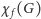 ) jest poza zasięgiem możliwości obliczeniowych dzisiejszych komputerów. Można wtedy stosować tzw. algorytmy przybliżone: takie, które działają w rozsądnym czasie, ale najpewniej nie podadzą nam najlepszego kolorowania, a jedynie jakieś "niezłe" (zazwyczaj używające o wiele większej liczby kolorów niż teoretycznie niezbędna).
) jest poza zasięgiem możliwości obliczeniowych dzisiejszych komputerów. Można wtedy stosować tzw. algorytmy przybliżone: takie, które działają w rozsądnym czasie, ale najpewniej nie podadzą nam najlepszego kolorowania, a jedynie jakieś "niezłe" (zazwyczaj używające o wiele większej liczby kolorów niż teoretycznie niezbędna).
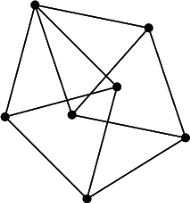
Ten graf wymaga czterech kolorów
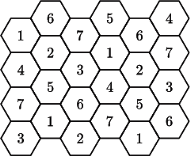
Siedem kolorów wystarczy (przekątne sześciokątów mają długość
Okazuje się, że w przypadku II można zaproponować tak naprawdę uniwersalną makietę wykorzystującą taką skończoną liczbę kolorów, która zadziała dla każdej, dowolnie skomplikowanej sieci nadajników. Nie jest to oczywiste, bowiem ogólnie dla każdego 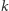 istnieje graf, który wymaga więcej niż
istnieje graf, który wymaga więcej niż 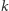 kolorów (i podobnie dla ułamkowej wersji kolorowania). Jednak geometryczne własności układu nadajników upraszczają sytuację.
kolorów (i podobnie dla ułamkowej wersji kolorowania). Jednak geometryczne własności układu nadajników upraszczają sytuację.
Kolorowanie płaszczyzny
Przed przedstawieniem wspomnianej makiety przyda się wstęp historyczny. Otóż w latach 60. XX wieku Edward Nelson zadał następujące pytanie:
Problem 2. Ile kolorów potrzeba, aby pokolorować (nieskończony) graf 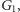 którego wierzchołkami są wszystkie punkty płaszczyzny euklidesowej
którego wierzchołkami są wszystkie punkty płaszczyzny euklidesowej 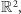 a dwa punkty/wierzchołki są połączone krawędzią, jeśli znajdują się w odległości dokładnie 1?
a dwa punkty/wierzchołki są połączone krawędzią, jeśli znajdują się w odległości dokładnie 1?
Być może w pierwszej chwili to zaskakuje, ale taki graf można pokolorować na 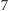 kolorów. Mimo sporego zainteresowania tym problemem nie udało się poprawić znanego od kilkudziesięciu lat oszacowania
kolorów. Mimo sporego zainteresowania tym problemem nie udało się poprawić znanego od kilkudziesięciu lat oszacowania 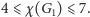
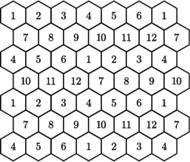
Najoszczędniejsze znane kolorowanie klasyczne (średnica sześciokątów to 1)
Dalszy tok działania będzie taki, że punkty na płaszczyźnie będą oznaczały wszelkie możliwe miejsca, gdzie może znaleźć się nadajnik. Postawmy pytanie: w jakiej odległości mogą się znajdować nadajniki konfliktowe, gdy zasięg każdego nadajnika jest równy 1? Potencjalnie konfliktowa jest każda para nadajników w odległości z przedziału 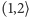 - tylko wtedy nadajniki nie mogą się kontaktować bezpośrednio, ale mogą (choć nie muszą) mieć inny nadajnik we wspólnym zasięgu. Zastąpmy więc graf
- tylko wtedy nadajniki nie mogą się kontaktować bezpośrednio, ale mogą (choć nie muszą) mieć inny nadajnik we wspólnym zasięgu. Zastąpmy więc graf 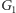 grafem
grafem 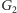 :
:
- zbiór wierzchołków to
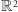 ;
; - krawędzią łączymy punkty leżące w odległości z przedziału
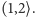
Kolorowanie tego grafu będzie stanowiło uniwersalną makietę: wystarczy położyć konkretną sieć na płaszczyźnie makiety, odczytać kolory poprawnego kolorowania tej sieci, a co za tym idzie, poprawny schemat nadawania.
Najpierw więc pokolorujmy 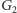 w klasyczny sposób. Oto najlepszy znany wynik.
w klasyczny sposób. Oto najlepszy znany wynik.
Takie kolorowanie daje uniwersalny cykl nadawania długości 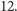

Teraz obejrzymy przykład oszczędności za pomocą ułamkowej wersji kolorowania.
Takie kolorowanie daje uniwersalny cykl nadawania długości

Rysunek wymaga objaśnienia, bo powinien być trójwymiarowy: Wyróżnione pary sześciokątów z liczbami od i do viii to fragmenty kolejnych warstw ułożonych z tych samych stu, ale oczywiście odpowiednio przesuniętych kolorów (te sześciokąty odpowiadają kolorom 1 i 2, a pozostałe są usytuowane względem nich tak, jak na dolnej warstwie) - warstw jest 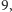 co oznacza, że każdy punkt ma
co oznacza, że każdy punkt ma 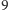 kolorów.
kolorów.
Rozwijając tę metodę, można znaleźć kolejne kolorowania, dążące do wartości 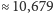 (np. dla
(np. dla 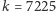 i
i 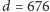 otrzymujemy jakość lepszą niż
otrzymujemy jakość lepszą niż 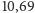 ).
).
Im większe 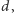 tym drobniejszy podział cyklu nadawania na kawałki - ale zbyt mocny podział może z technicznych powodów być niemożliwy do zastosowania.
tym drobniejszy podział cyklu nadawania na kawałki - ale zbyt mocny podział może z technicznych powodów być niemożliwy do zastosowania.
Dla bardziej skomplikowanych figur i naprawdę bardzo dużych 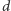 można jednak zejść nawet poniżej
można jednak zejść nawet poniżej 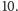
Na koniec warto zwrócić uwagę na fakt, iż zastosowanie uniwersalnej makiety nie tylko nie wymaga obliczeń dla każdej nowej sieci, ale nawet działa w przypadku nadajników ruchomych - nie trzeba niczego wyliczać na nowo, wystarczy uwzględniać przesuwanie się nadajników zgodnie z makietą. Czasem teoria ma naprawdę wielką siłę!