Niewiadomą w tym równaniu jest prędkość (a także ciśnienie) w dowolnej chwili 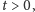 przy czym zakładamy, że prędkość płynu w chwili 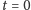jest nam dana, podobnie jak prędkość płynu na brzegu obszaru (przyjmujemy zwykle, że jest ona stale zerowa). Cały opis przepływu opiera się na założeniu, że w każdej chwili (a jest ich, oczywiście, nieskończenie wiele) i w każdym punkcie obszaru (a punktów takich jest także nieskończenie wiele) można określić wektor prędkości płynu. To, co chcielibyśmy od naszego modelu, to

1)

jednoznaczność, która zakłada, że gdy określony jest z całą dokładnością przepływ w chwili 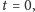 to przypisanie wektorów prędkości w każdej chwili 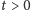można zrobić tylko na jeden sposób;

2)

brak wybuchów: jeśli początkowa prędkość jest ograniczona i zmienia się w gładki sposób od punktu do punktu (tzn. prędkość i jej pochodne są ciągłe), to w każdym momencie w przyszłości prędkość jest ograniczona.

Warunki 1) oraz 2) wydają się niezbyt restrykcyjne, a mimo to od niemal 200 lat nie udało się wykazać, że istotnie są one spełnione (wiadomo, że jest tak dla przepływów dwuwymiarowych, ale nas, oczywiście, interesuje świat trójwymiarowy).

Już z tego pobieżnego opisu widać, że w opisywanej tu dziedzinie stosunek do nieskończoności jest dość ambiwalentny. Z jednej strony chętnie akceptujemy fakt, że nasz opis przepływu opiera się na założeniu, że płyn stanowi continuum złożone z nieskończenie wielu punktów, a czas płynie w sposób ciągły. Akceptacja ta jest radosna, bo raczej nikt nie bierze na poważnie możliwości śledzenia ruchu pojedynczych cząsteczek płynu: ich liczba, choć skończona, wydaje się dużo bardziej przerażająca od nieskończoności. Z drugiej strony nerwowo reagujemy na sugestie, że przepływ mógłby wygenerować (lokalnie) nieskończoną prędkość. Ponieważ mówimy tu o podstawowym równaniu hydrodynamiki, więc nie jest zaskakujące, że niedawno ogłoszono nawet nagrodę dla tego, kto raz na zawsze wyeliminuje nieskończone wektory prędkości z równania Naviera–Stokesa (lub wykaże, że takowe jednak mogą się pojawić – wtedy cały model stanie pod znakiem zapytania).

Zanim jednak nastąpi ostateczne rozwiązanie tego problemu, warto wspomnieć o tym, jak do tej pory niechcianą nieskończoność próbowano poddać rozmaitym ograniczeniom. Po pierwsze (to stary wynik Leraya z 1934 roku), okazało się, że hipotetyczny zbiór czasów 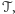 w których prędkość wybucha, nawet jeśli jest niepusty, to przynajmniej jest bardzo mały w następującym sensie:

Dla dowolnie małej liczby 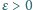 można znaleźć serię odcinków o długościach: 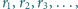 które całkowicie przykrywają zbiór 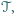 a przy tym

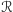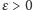Po drugie, wykazano (dużo później, bo w 1982 roku; to wynik Caffarellego, Kohna i Nirenberga), że zbiór punktów czasoprzestrzeni, w których ewentualnie dochodzi do wybuchu prędkości, też jest bardzo mały, tak że dla dowolnie małej liczby można znaleźć serię czterowymiarowych walców mających w „podstawie” kulę o promieniu 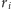oraz o „wysokości” w czasie równej 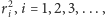które całkowicie przykrywają zbiór 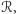 a przy tym

W ten sposób niechciana nieskończoność w równaniu Naviera–Stokesa została częściowo ograniczona w swej wolności. Czy zostanie całkiem wyeliminowana – pokaże przyszłość.