Jest to jedna z metod tak zwanego dzielenia sekretu. Na przykład jeśli prezes banku chce, by dwaj wiceprezesi mogli otworzyć sejf tylko wspólnie (żadnemu w pełni nie ufa), może każdemu dać jedną z folii szyfrujących tajny kod dostępu

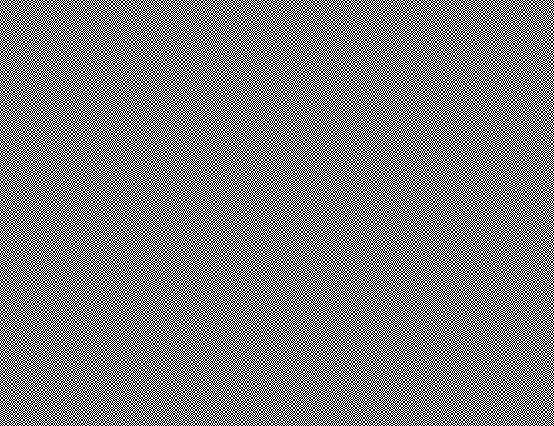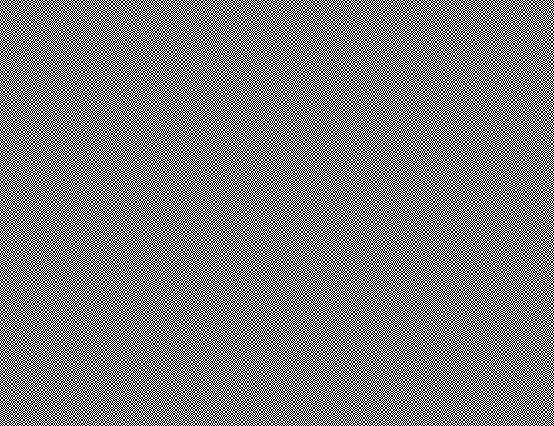
Animacja obu obrazków (w większej rozdzielczości)

Rys. 2 Cegiełki służące do tworzenia udziałów. Białe części są przezroczyste.

Jeśli cegiełki mają 2 na 2 piksele, otrzymamy udziały o bokach dwukrotnie większych niż szyfrowany obraz.

Jak szyfrować?

W najprostszej wersji szyfruje się obraz dwukolorowy, czarno-biały. Dzielimy go na maleńkie kwadraciki (piksele), z których każdy jest w całości czarny lub biały. Następnie, analizując wyjściowy obraz piksel po pikselu, tworzymy komputerowo dwa nowe obrazy, nazwijmy je udziałami. Jeśli dany piksel jest biały, w odpowiadającym mu miejscu obydwu udziałów umieszczamy takie same kwadraty (nazwijmy je cegiełkami), losowo wybierając z dwóch przedstawionych na rysunku 2. Dla czarnego piksela w odpowiednich miejscach udziałów umieszczamy różne cegiełki, losowo decydując o tym, która na którym udziale.

Dlaczego to działa?

Gdy nałożymy tak utworzone udziały, w miejscach odpowiadających czarnym pikselom będą całkowicie czarne (bo czarne części cegiełek dopełniają się), zaś zamiast białych pikseli zobaczymy kwadraty czarno-białe (bo nałożą się dwie identyczne cegiełki) i tak małe, że praktycznie szare. W rezultacie szyfrowany czarno-biały obraz odczytamy jako obraz czarno-szary.

Czy da się złamać ten szyfr?

W każdym miejscu każdego z udziałów o tym, która z cegiełek się pojawi, decydujemy losowo. Wobec tego osoba posiadająca jeden udział nie może się z niego niczego dowiedzieć. Cała informacja ukryta jest „pomiędzy” udziałami — w tym, gdzie cegiełki na nich są te same, a gdzie różne.

Dzięki temu kryptografii wizualnej można używać też do szyfrowania listów. Jeśli Bob wyrusza w podróż, przed wyjazdem generuje duży pstrokaty prostokąt, losowo wybierając cegiełki (to będzie klucz do szyfrowania i rozszyfrowywania). Zostawia go Alicji na folii, a sam ma kopię w swoim komputerze. Gdy zechce przesłać tajny list, potraktuje ten prostokąt jako pierwszy udział listu i wygeneruje odpowiedni drugi udział (podobiera takie same lub dopełniające cegiełki). Prześle go Alicji na folii, którą ona nałoży na pierwszą folię i odczyta list. Jeśli przesyłka z drugą folią wpadnie w niepowołane ręce, jest nie do odczytania.

Na zakończenie

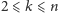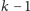Bardziej zaawansowane wersje kryptografii wizualnej pozwalają szyfrować obrazy w odcieniach szarości, a nawet kolorowe. Można też dzielić sekret na więcej niż dwie części, a także dzielić go na  części tak, by dowolnych  wystarczało do odczytania wiadomości ( ), ale żadnych   nie wystarczało. Wreszcie można ukrywać sam fakt przesyłania wiadomości, tworząc zamiast budzących podejrzenia pstrokatych udziałów dwa „zwykłe” obrazy, które po nałożeniu znikają, a oczom odbiorcy ukazuje się tajny przekaz.

Dziękuję Kubie Pochrybniakowi za wykonanie rysunku 1.