Układy iterowanych przekształceń

Solkoll / wikipedia
Kto coś słyszał o fraktalach, zwykle potrafi wymienić dwie ich cechy charakterystyczne: figury te mają skomplikowany kształt (bardziej wtajemniczeni mówią o ułamkowym wymiarze; kto chce być bardziej wtajemniczony, przeczyta artykuł Krzysztofa Barańskiego na stronie 4) i wykazują samopodobieństwo (bardziej wtajemniczeni umieją powiedzieć, jakiego rodzaju: geometryczne, afiniczne, rzutowe, a może stochastyczne). Mówiąc ogólnie, cechy te ma również wiele obiektów spotykanych w świecie, a to otwiera szerokie pole do zastosowań fraktali w grafice komputerowej. Jej celem jest przecież naśladowanie rzeczywistości.
Zajmiemy się najprostszą metodą konstruowania i obrazowania fraktali, za pomocą układów iterowanych przekształceń (ang. iterated function systems, w skrócie IFS). U podstaw tej metody leży kilka twierdzeń. Choć twierdzenia te są niebanalne, ich dowody są niezbyt trudne, a komputerowe algorytmy generowania fraktali za pomocą IFS-ów są jeszcze prostsze.
Zacznijmy od ustalenia, co uważamy za fraktal. Przyjmiemy, że jest nim
dowolny niepusty, domknięty i ograniczony zbiór punktów płaszczyzny
euklidesowej
 Zwróćmy uwagę, że w ten sposób za fraktale
uznaliśmy także bardzo „porządne” figury, takie jak wielokąty, których
wymiar nie jest ułamkiem. Odrzucenie takich figur (przez kogoś, komu
zależy tylko na „prawdziwych” fraktalach) bardzo (i niepotrzebnie)
skomplikowałoby teorię, a poza tym w grafice zwykłe wielokąty też się
przydadzą, prawda?
Zwróćmy uwagę, że w ten sposób za fraktale
uznaliśmy także bardzo „porządne” figury, takie jak wielokąty, których
wymiar nie jest ułamkiem. Odrzucenie takich figur (przez kogoś, komu
zależy tylko na „prawdziwych” fraktalach) bardzo (i niepotrzebnie)
skomplikowałoby teorię, a poza tym w grafice zwykłe wielokąty też się
przydadzą, prawda?
Niech
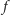 oznacza ciągłe przekształcenie płaszczyzny w siebie. Jeśli
zatem
oznacza ciągłe przekształcenie płaszczyzny w siebie. Jeśli
zatem
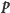 oznacza dowolny punkt płaszczyzny, to
oznacza dowolny punkt płaszczyzny, to
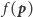 jest
również jej punktem. Od razu zauważamy, że funkcja
jest
również jej punktem. Od razu zauważamy, że funkcja
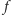 wyznacza
również przekształcenie zbioru wszystkich figur w płaszczyźnie w ten
sam zbiór; jeśli
wyznacza
również przekształcenie zbioru wszystkich figur w płaszczyźnie w ten
sam zbiór; jeśli
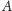 jest figurą (tj. dowolnym zbiorem punktów
płaszczyzny), to
jest figurą (tj. dowolnym zbiorem punktów
płaszczyzny), to
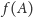 też jest figurą, która składa się z punktów
też jest figurą, która składa się z punktów
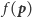 dla wszystkich punktów
dla wszystkich punktów
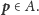 Zauważmy też, że jeśli
figura
Zauważmy też, że jeśli
figura
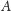 jest fraktalem (zgodnie z przyjętą definicją), to figura
jest fraktalem (zgodnie z przyjętą definicją), to figura
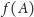 również nim jest.
również nim jest.
Oznaczymy literą
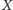 zbiór wszystkich fraktali na płaszczyźnie
i zajmiemy się problemem mierzenia odległości między fraktalami. W tym
celu określmy epsilonowe rozszerzenie figury. Niech
zbiór wszystkich fraktali na płaszczyźnie
i zajmiemy się problemem mierzenia odległości między fraktalami. W tym
celu określmy epsilonowe rozszerzenie figury. Niech
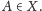 Dla
dowolnego
Dla
dowolnego
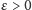 możemy każdy punkt figury
możemy każdy punkt figury
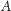 nakryć
kołem o promieniu
nakryć
kołem o promieniu
 (biorąc koło o środku w nakrywanym
punkcie). Epsilonowe rozszerzenie figury
(biorąc koło o środku w nakrywanym
punkcie). Epsilonowe rozszerzenie figury
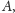 które oznaczymy
które oznaczymy
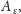 jest sumą tych wszystkich kół. Dla
jest sumą tych wszystkich kół. Dla
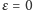 przyjmujemy
przyjmujemy
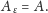 Dla dowolnych dwóch fraktali,
Dla dowolnych dwóch fraktali,
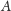 i
i
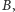 istnieje takie
nieujemne
istnieje takie
nieujemne
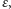 że
że
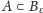 oraz
oraz
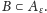 Najmniejsze takie
Najmniejsze takie
 przyjmiemy za odległość figur
przyjmiemy za odległość figur
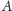 i
i
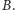 W ten
sposób w zbiorze
W ten
sposób w zbiorze
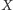 określiliśmy metrykę (tzw. metrykę
Hausdorffa), którą oznaczymy symbolem
określiliśmy metrykę (tzw. metrykę
Hausdorffa), którą oznaczymy symbolem
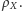 Łatwo jest zauważyć, do
czego są tu potrzebne założenia, że fraktale są niepuste i ograniczone.
Założenie, iż są one domknięte, jest potrzebne m.in. po to, aby z równości
Łatwo jest zauważyć, do
czego są tu potrzebne założenia, że fraktale są niepuste i ograniczone.
Założenie, iż są one domknięte, jest potrzebne m.in. po to, aby z równości
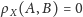 wynikało, że
wynikało, że
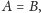 i abyśmy mieli w zbiorze
i abyśmy mieli w zbiorze
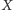 wszystkie zbiory jednopunktowe.
wszystkie zbiory jednopunktowe.
Mamy zatem dwie różne przestrzenie metryczne: płaszczyznę
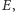 w której
odległość (punktów) mierzymy w zwykły sposób (tę metrykę oznaczymy
w której
odległość (punktów) mierzymy w zwykły sposób (tę metrykę oznaczymy
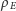 ), i przestrzeń
), i przestrzeń
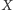 z metryką
z metryką
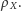 Zauważmy, że dla
dowolnych punktów
Zauważmy, że dla
dowolnych punktów
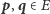 jest
jest
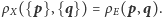 Możemy
wybrać dowolne przekształcenia ciągłe
Możemy
wybrać dowolne przekształcenia ciągłe
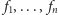 płaszczyzny
płaszczyzny
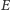 w siebie; przekształceniom tym odpowiadają przekształcenia
w siebie; przekształceniom tym odpowiadają przekształcenia
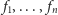 przestrzeni
przestrzeni
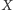 w siebie. Użyjemy ich do określenia
kolejnego przekształcenia
w siebie. Użyjemy ich do określenia
kolejnego przekształcenia
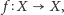 przyjmując, że dla dowolnej figury
przyjmując, że dla dowolnej figury
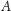 jest
jest

Definicja. Mówimy, że przekształcenie
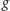 (dowolnej) przestrzeni
metrycznej (z metryką
(dowolnej) przestrzeni
metrycznej (z metryką
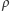 ) jest zwężające, jeśli
istnieje taka stała
) jest zwężające, jeśli
istnieje taka stała
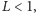 że dla dowolnych punktów
że dla dowolnych punktów
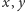 tej
przestrzeni zachodzi
tej
przestrzeni zachodzi
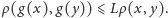
Udowodnimy
Twierdzenie (Twierdzenie Hutchinsona). Przekształcenie
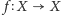 jest
zwężające, jeśli wszystkie przekształcenia
jest
zwężające, jeśli wszystkie przekształcenia
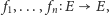 użyte
do zdefiniowania przekształcenia
użyte
do zdefiniowania przekształcenia
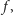 są zwężające.
są zwężające.
Dowód. Przypuśćmy, że
przekształcenia
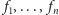 są zwężające. Zatem istnieje taka liczba
są zwężające. Zatem istnieje taka liczba
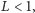 że dla dowolnych punktów
że dla dowolnych punktów
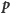 i
i
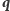 oraz dla
oraz dla
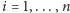 jest
jest
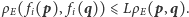 Niech
Niech
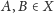 i niech
i niech
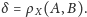 Stąd dla każdego punktu
Stąd dla każdego punktu
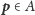 istnieje
taki punkt
istnieje
taki punkt
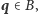 że
że
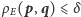 (na przykład, należący
do
(na przykład, należący
do
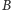 środek koła o promieniu
środek koła o promieniu
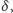 w którym leży punkt
w którym leży punkt
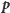 ).
Ale wtedy dla każdego
).
Ale wtedy dla każdego
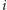 mamy
mamy
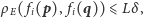 skąd
wynika, że figura
skąd
wynika, że figura
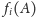 jest zawarta w epsilonowym rozszerzeniu
jest zawarta w epsilonowym rozszerzeniu
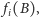 dla
dla
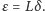 Możemy więc napisać
Możemy więc napisać

i podobnie dowodzimy, że
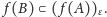 Stąd
Stąd
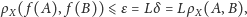
co kończy dowód.
Drugie z najważniejszych twierdzeń leżących u podstaw układów iterowanych przekształceń to
Twierdzenie (Twierdzenie Banacha o punkcie stałym). W zupełnej przestrzeni metrycznej dowolne przekształcenie zwężające ma jednoznacznie określony punkt stały.
Nie będziemy dowodzili tu tego twierdzenia, podobnie jak faktu, że zbiór
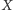 z metryką
z metryką
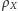 jest zupełną przestrzenią metryczną (choć nie są
to trudne dowody). Punkt stały przekształcenia
jest zupełną przestrzenią metryczną (choć nie są
to trudne dowody). Punkt stały przekształcenia
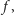 określonego zgodnie
z opisem podanym wyżej, jest fraktalem, tj. pewną figurą niepustą, domkniętą
i ograniczoną; oznaczmy ją literą
określonego zgodnie
z opisem podanym wyżej, jest fraktalem, tj. pewną figurą niepustą, domkniętą
i ograniczoną; oznaczmy ją literą
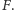 Z jakich punktów składa się ta
figura? Przekształcenia
Z jakich punktów składa się ta
figura? Przekształcenia
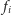 są zwężające, a zatem każde z nich ma jeden
punkt stały w płaszczyźnie
są zwężające, a zatem każde z nich ma jeden
punkt stały w płaszczyźnie
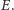 Punkty te, oczywiście, należą do figury
Punkty te, oczywiście, należą do figury
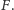 Weźmy dowolne (skończone) złożenie naszych przekształceń,
Weźmy dowolne (skończone) złożenie naszych przekształceń,
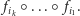 Ono też jest przekształceniem zwężającym płaszczyzny
Ono też jest przekształceniem zwężającym płaszczyzny
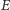 i jego punkt stały również należy do
i jego punkt stały również należy do
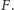 Można dowieść,
że figura
Można dowieść,
że figura
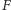 jest domknięciem zbioru punktów stałych wszystkich
takich złożeń.
jest domknięciem zbioru punktów stałych wszystkich
takich złożeń.
Poza ciągłością, a potem własnością zwężania, nie nakładaliśmy
żadnych warunków na przekształcenia
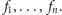 Najczęściej
w praktyce IFS-y są budowane z przekształceń afinicznych. Każde
afiniczne przekształcenie płaszczyzny może być reprezentowane za
pomocą sześciu (czyli niewielu) liczb i obliczenia z nim związane zabierają
bardzo mało czasu. Ma miejsce jeszcze jeden istotny fakt, którego ścisły
dowód jest, niestety, dosyć żmudny: figura
Najczęściej
w praktyce IFS-y są budowane z przekształceń afinicznych. Każde
afiniczne przekształcenie płaszczyzny może być reprezentowane za
pomocą sześciu (czyli niewielu) liczb i obliczenia z nim związane zabierają
bardzo mało czasu. Ma miejsce jeszcze jeden istotny fakt, którego ścisły
dowód jest, niestety, dosyć żmudny: figura
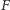 zależy od liczb
reprezentujących przekształcenia
zależy od liczb
reprezentujących przekształcenia
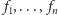 w sposób ciągły. Bardzo małe
zaburzenia tych liczb powodują zatem niewielkie zmiany otrzymanych
obrazów.
w sposób ciągły. Bardzo małe
zaburzenia tych liczb powodują zatem niewielkie zmiany otrzymanych
obrazów.
Przejdźmy do praktyki: aby określić IFS, wybieramy na płaszczyźnie jeden
duży trójkąt i
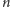 mniejszych; te mniejsze trójkąty przyjmujemy za
obrazy trójkąta dużego, co określa poszczególne przekształcenia
afiniczne.
mniejszych; te mniejsze trójkąty przyjmujemy za
obrazy trójkąta dużego, co określa poszczególne przekształcenia
afiniczne.
Istnieje kilka metod tworzenia obrazu figury
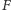 ; wszystkie one polegają na
iterowaniu przekształceń
; wszystkie one polegają na
iterowaniu przekształceń
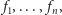 czyli stosowaniu ich do pewnej
figury, a potem do jej obrazów w przekształceniach wykonanych wcześniej.
Możemy zacząć od figury jednopunktowej. Najlepiej jest przyjąć, że składa
się ona z punktu stałego dowolnego z przekształceń
czyli stosowaniu ich do pewnej
figury, a potem do jej obrazów w przekształceniach wykonanych wcześniej.
Możemy zacząć od figury jednopunktowej. Najlepiej jest przyjąć, że składa
się ona z punktu stałego dowolnego z przekształceń
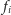 – punkt ten
łatwo jest znaleźć, rozwiązując układ dwóch równań liniowych, a jeśli
zaczniemy od niego, to wszystkie kolejno otrzymane punkty będą należeć do
figury
– punkt ten
łatwo jest znaleźć, rozwiązując układ dwóch równań liniowych, a jeśli
zaczniemy od niego, to wszystkie kolejno otrzymane punkty będą należeć do
figury
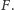
Metoda I. W każdej iteracji rysujemy bieżący punkt
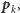 a następnie losujemy liczbę
a następnie losujemy liczbę
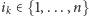 i obliczamy
i obliczamy
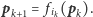 Metoda ta potrzebuje bardzo mało pamięci. Jej wadą
jest konieczność starannego dobrania rozkładu prawdopodobieństwa
do losowania. Jeśli rozkład jest dobrze dobrany, to zwykle wystarczy
wykonać od kilkunastu tysięcy do kilkuset tysięcy iteracji.
Metoda ta potrzebuje bardzo mało pamięci. Jej wadą
jest konieczność starannego dobrania rozkładu prawdopodobieństwa
do losowania. Jeśli rozkład jest dobrze dobrany, to zwykle wystarczy
wykonać od kilkunastu tysięcy do kilkuset tysięcy iteracji.
Metoda II.
Użyjemy kolejki, do której wstawimy punkt
 W każdej
iteracji wyjmujemy punkt z kolejki, obliczamy jego obrazy we wszystkich
przekształceniach
W każdej
iteracji wyjmujemy punkt z kolejki, obliczamy jego obrazy we wszystkich
przekształceniach
 każdy z nich wstawiamy do kolejki
i rysujemy. Potrzebna jest zatem kolejka mogąca pomieścić prawie tyle
punktów, ile chcemy wyznaczyć (zwykle co najmniej kilka tysięcy).
każdy z nich wstawiamy do kolejki
i rysujemy. Potrzebna jest zatem kolejka mogąca pomieścić prawie tyle
punktów, ile chcemy wyznaczyć (zwykle co najmniej kilka tysięcy).
Metoda III. Podobnie jak w metodzie drugiej, użyjemy kolejki;
nowością jest to, że wcześniej ustalamy wielkość (w pikselach)
obrazu, który chcemy uzyskać. Obliczenia prowadzimy w układzie
współrzędnych obrazu i po obliczeniu każdego punktu zaokrąglamy
jego współrzędne do liczb całkowitych. Do kolejki wstawiamy tylko
te piksele, które nie były zamalowane wcześniej. W tej metodzie
wykonamy skończenie wiele iteracji – algorytm zakończy działanie po
opróżnieniu kolejki. Otrzymany rysunek jest najlepszym przybliżeniem
figury
 przy ustalonej rozdzielczości rastra. Stosując tę i następną
metodę, należy zadbać o to, aby cała figura
przy ustalonej rozdzielczości rastra. Stosując tę i następną
metodę, należy zadbać o to, aby cała figura
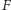 zmieściła się
na obrazie.
zmieściła się
na obrazie.
Metoda IV. Rysujemy
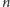 poteksturowanych
równoległoboków, będących obrazami prostokąta, w którym tworzymy
obraz, w przekształceniach
poteksturowanych
równoległoboków, będących obrazami prostokąta, w którym tworzymy
obraz, w przekształceniach
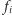 ; otrzymanego obrazu używamy
jako teksturę w następnej iteracji. W tej metodzie wystarczy wykonać
kilkanaście lub najwyżej kilkadziesiąt iteracji. Kolejka nie jest tu
potrzebna, ale bardzo się przydaje zrównoleglenie obliczeń przy użyciu
nowoczesnej karty graficznej.
; otrzymanego obrazu używamy
jako teksturę w następnej iteracji. W tej metodzie wystarczy wykonać
kilkanaście lub najwyżej kilkadziesiąt iteracji. Kolejka nie jest tu
potrzebna, ale bardzo się przydaje zrównoleglenie obliczeń przy użyciu
nowoczesnej karty graficznej.
Zobaczmy kilka przykładowych obrazków.
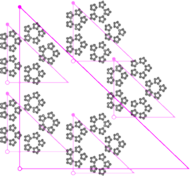
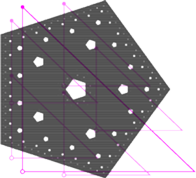
Rys. 1
Na rysunku 1 mamy dwa fraktale otrzymane za pomocą układów pięciu
przekształceń. Każde przekształcenie jest złożeniem jednokładności
o skali
 i przesunięcia, przemieszczającego pewien punkt na jeden
z pięciu punktów rozmieszczonych równomiernie na okręgu. Z lewej
strony mamy
i przesunięcia, przemieszczającego pewien punkt na jeden
z pięciu punktów rozmieszczonych równomiernie na okręgu. Z lewej
strony mamy
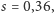 a z prawej
a z prawej
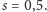 Zwiększając dalej
Zwiększając dalej
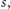 otrzymalibyśmy pięciokąt foremny.
otrzymalibyśmy pięciokąt foremny.
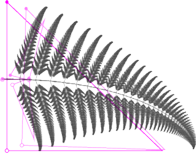
Najbardziej znanymi fraktalami, które można otrzymać, iterując
przekształcenia afiniczne, są paprocie Barnsleya, generowane przez układy
czterech przekształceń, ale można też „hodować” w ten sposób
inne rośliny; już dla
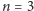 można uzyskać ciekawe efekty
(Rys. 2).
można uzyskać ciekawe efekty
(Rys. 2).
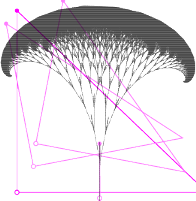
Figury o skomplikowanym kształcie można zatem reprezentować przy użyciu bardzo niewielkiej ilości danych. Obrazek na rysunku 3 przedstawia figury wygenerowane za pomocą pewnej liczby IFS-ów, których opis składa się z dwustu kilkudziesięciu liczb rzeczywistych.

Rys. 5
Rozwinięciem układów iterowanych przekształceń są algorytmy fraktalnej kompresji obrazów – są to jedne z najskuteczniejszych stosowanych obecnie technik kompresji. Umożliwiają one zapisywanie reprezentacji obrazów w małej ilości miejsca, a potem odtwarzanie tych obrazów z małym błędem. Oczywistą różnicą wobec IFS-ów jest przejście od określonych na płaszczyźnie funkcji przyjmujących tylko dwie wartości (punkt albo należy, albo nie należy do ustalonej figury) do funkcji przyjmujących wartości rzeczywiste. Tak samo, jak w przypadku fraktali generowanych przez IFS-y, gdzie krótki ciąg liczb reprezentujących poszczególne przekształcenia afiniczne umożliwia wygenerowanie obrazu figury o skomplikowanym kształcie, zapisane przez procedurę kompresji dane reprezentują pewne przekształcenie zwężające zbioru funkcji (obrazów) w siebie. Punktem stałym tego przekształcenia jest przybliżenie obrazu poddanego kompresji. Odtwarzanie obrazu polega na wykonaniu kilku lub kilkunastu iteracji tego przekształcenia.