Nagrody Nobla
Polowanie na jelenia i równowagi Nasha

wikipedia
John Forbes Nash, Jr.
W 1762 roku Jean Jacques Rousseau napisał: „Polujący na jelenia myśliwi są w pełni świadomi, że aby go upolować, muszą być lojalni wobec siebie i pozostać na swoich posterunkach. Jeżeli jednak zając przebiegnie w pobliżu jednego z nich, nie ma wątpliwości, że myśliwy ten ruszy za pewną zdobyczą, doprowadzając do fiaska polowanie na jelenia.” Przetłumaczmy to na język współczesnej teorii gier...
Aby sprecyzować model teoriogrowy, musimy określić zbiór
graczy
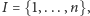 zbiór dostępnych im strategii
zbiór dostępnych im strategii
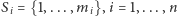 oraz funkcje wypłat
oraz funkcje wypłat
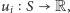 gdzie
gdzie
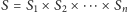 ; wypłata każdego gracza zależy nie tylko od
jego strategii, lecz również od strategii wszystkich jego oponentów, to
znaczy profilu strategii
; wypłata każdego gracza zależy nie tylko od
jego strategii, lecz również od strategii wszystkich jego oponentów, to
znaczy profilu strategii
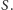 W naszym przypadku każdy z dwóch
myśliwych ma do dyspozycji dwie strategie: jelenia (J) albo zająca (Z). Aby
podać funkcję wypłat, musimy wpierw przypisać obu nieszczęsnym
zwierzętom określoną wartość. Niech jeleń będzie wart
W naszym przypadku każdy z dwóch
myśliwych ma do dyspozycji dwie strategie: jelenia (J) albo zająca (Z). Aby
podać funkcję wypłat, musimy wpierw przypisać obu nieszczęsnym
zwierzętom określoną wartość. Niech jeleń będzie wart
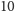 jednostek
ekonomicznej użyteczności, a zając
jednostek
ekonomicznej użyteczności, a zając
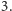 Upolowany jeleń dzielony jest
równo między dwóch graczy ze strategią J, zając przypada w całości
każdemu graczowi ze strategią Z. Funkcja wypłat przybiera wtedy postać
macierzy
Upolowany jeleń dzielony jest
równo między dwóch graczy ze strategią J, zając przypada w całości
każdemu graczowi ze strategią Z. Funkcja wypłat przybiera wtedy postać
macierzy
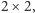 której element
której element
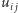 jest wypłatą gracza
pierwszego (wierszowego) grającego strategią
jest wypłatą gracza
pierwszego (wierszowego) grającego strategią
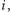 podczas gdy gracz drugi
(kolumnowy) gra strategią
podczas gdy gracz drugi
(kolumnowy) gra strategią
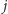 :
:

Gra jest symetryczna, co oznacza, że wypłaty gracza drugiego są dane przez macierz transponowaną do U. Gra jest rozgrywana w ten sposób, że gracze jednocześnie ogłaszają swoje strategie i dostają odpowiednie wypłaty. Macierz wypłat jest znana każdemu graczowi, który wie, że każdy z jego oponentów ją zna, wie, iż jego oponenci wiedzą, że on ją zna...
Pojawia się naglące pytanie: Jak grać? John Nash zaproponował następującą definicję równowagi. W równowadze Nasha, przy ustalonych strategiach przeciwników, żadnemu z graczy nie opłaca się zmienić swojej strategii. Formalnie:
Definicja.
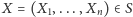 jest równowagą Nasha, jeśli dla
każdego
jest równowagą Nasha, jeśli dla
każdego
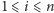 i
i
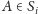
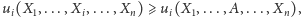 gdzie
gdzie
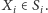
W naszym przykładzie mamy dwie równowagi Nasha:
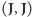 i
i
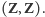 Stajemy więc przed problemem wyboru jednej z nich. Pierwsza
równowaga daje nam największe wypłaty, druga natomiast jest dominująca ze
względu na ryzyko – pojęcie zaproponowane przez Seltena i Harsanyi’ego.
Zakładamy, że przeciwnik z jednakowym prawdopodobieństwem
Stajemy więc przed problemem wyboru jednej z nich. Pierwsza
równowaga daje nam największe wypłaty, druga natomiast jest dominująca ze
względu na ryzyko – pojęcie zaproponowane przez Seltena i Harsanyi’ego.
Zakładamy, że przeciwnik z jednakowym prawdopodobieństwem
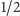 zagra jedną z dwóch strategii. Wybieramy strategię, która daje nam
większą wartość średnią. W naszym przypadku średnia wypłata dla
strategii Z wynosi
zagra jedną z dwóch strategii. Wybieramy strategię, która daje nam
większą wartość średnią. W naszym przypadku średnia wypłata dla
strategii Z wynosi
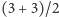 i jest większa od średniej wypłaty dla
strategii J równej
i jest większa od średniej wypłaty dla
strategii J równej
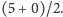 Warto wspomnieć, że za swój wkład
w teorię gier John Nash, Reinhard Selten i John Harsanyi zostali uhonorowani
w 1994 roku Nagrodą Nobla z ekonomii.
Warto wspomnieć, że za swój wkład
w teorię gier John Nash, Reinhard Selten i John Harsanyi zostali uhonorowani
w 1994 roku Nagrodą Nobla z ekonomii.
Ostatnio zostało zaproponowanych kilka modeli dynamicznych, w których tylko niektóre równowagi Nasha danej gry są stabilnymi punktami stacjonarnymi, a więc zostają wybrane. Badaniem dynamicznego dochodzenia do równowag Nasha zajmuje się ewolucyjna teoria gier, o której, być może, napiszemy w przyszłości.
Wnikliwy Czytelnik zada oczywiście pytanie, czy każda gra ma równowagę Nasha. W odpowiedzi poprosimy wnikliwego Czytelnika o skonstruowanie dwóch gier niemających równowag Nasha: symetrycznej gry z trzema strategiami oraz gry niesymetrycznej (wypłaty dla gracza wierszowego i kolumnowego dane są przez dwie niezależne macierze) z dwiema strategiami.
Aby tradycji matematycznej stało się zadość i wystąpiło twierdzenie
o istnieniu, wprowadźmy strategie mieszane. Strategia mieszana
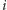 -tego
gracza to rozkład prawdopodobieństwa na zbiorze strategii czystych
-tego
gracza to rozkład prawdopodobieństwa na zbiorze strategii czystych
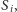 czyli
czyli
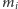 nieujemnych liczb
nieujemnych liczb
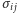 sumujących się do
sumujących się do
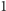 ;
;
 jest prawdopodobieństwem, z jakim
jest prawdopodobieństwem, z jakim
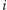 -ty gracz zagra
strategią
-ty gracz zagra
strategią
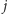 -tą. Przyjmujemy, że wypłata z profilu strategii mieszanych
dana jest przez jej wartość oczekiwaną i uogólniamy w oczywisty
sposób definicję równowagi Nasha, podstawiając w niej
-tą. Przyjmujemy, że wypłata z profilu strategii mieszanych
dana jest przez jej wartość oczekiwaną i uogólniamy w oczywisty
sposób definicję równowagi Nasha, podstawiając w niej
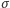 za
za
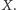 Zachodzi wtedy następujące
Zachodzi wtedy następujące
Twierdzenie. Każda gra ze skończoną liczbą graczy i strategii ma co najmniej jedną równowagę Nasha w strategiach mieszanych.
Dowód wykorzystuje jedno z twierdzeń o punkcie stałym (równowaga Nasha jest najlepszą odpowiedzią na równowagę Nasha).
Ambitnego Czytelnika poprosimy teraz o znalezienie wszystkich równowag Nasha dla dowolnej symetrycznej gry dwuosobowej z dwiema strategiami. Udowodni on w ten sposób powyższe twierdzenie dla tej klasy gier.
Przenieśmy się teraz z osiemnastowiecznego lasu do współczesnego miasta,
gdzie dwóch pracowników właśnie zasiadło do wykończenia wspólnego
projektu. Każdy z nich może albo pracować,
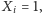 albo oszukiwać,
czyli pozorować pracę,
albo oszukiwać,
czyli pozorować pracę,
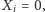
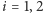 ; praca wymaga inwestycji
; praca wymaga inwestycji
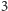 jednostek naszej użyteczności. Przychód z wykonanego projektu
jednostek naszej użyteczności. Przychód z wykonanego projektu
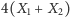 jest dzielony równo między partnerów. Powyższa gra ma
następujące przedstawienie macierzowe:
jest dzielony równo między partnerów. Powyższa gra ma
następujące przedstawienie macierzowe:

Jedyną równowagą Nasha jest profil
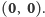 Zauważmy, że w przypadku
pracy obu partnerów ich wypłata jest większa. Profil
Zauważmy, że w przypadku
pracy obu partnerów ich wypłata jest większa. Profil
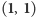 nie jest jednak
równowagą Nasha. Staramy się więc działać racjonalnie, grać strategią w
jedynej równowadze Nasha i efektem tego jest obustronny brak korzyści.
Powyższa gra znana jest pod nazwą Dylematu Więźnia. Aby zrozumieć
występowanie zachowań altruistycznych w układach rywalizujących jednostek,
zaproponowano ostatnio proste modele dynamiczne, w których stabilne punkty
równowagi nie są równowagami Nasha. Przeszliśmy więc od problemu
wyboru jednej z równowag Nasha do problemu znalezienia równowagi nie
będącej równowagą Nasha. Analiza dynamicznych strategii prowadzących do
współpracy w powtarzanej grze typu Dylemat Więźnia wymaga oddzielnego
omówienia.
nie jest jednak
równowagą Nasha. Staramy się więc działać racjonalnie, grać strategią w
jedynej równowadze Nasha i efektem tego jest obustronny brak korzyści.
Powyższa gra znana jest pod nazwą Dylematu Więźnia. Aby zrozumieć
występowanie zachowań altruistycznych w układach rywalizujących jednostek,
zaproponowano ostatnio proste modele dynamiczne, w których stabilne punkty
równowagi nie są równowagami Nasha. Przeszliśmy więc od problemu
wyboru jednej z równowag Nasha do problemu znalezienia równowagi nie
będącej równowagą Nasha. Analiza dynamicznych strategii prowadzących do
współpracy w powtarzanej grze typu Dylemat Więźnia wymaga oddzielnego
omówienia.