Obaj laureaci znakomitą większość swoich prac publikowali w okresie, w którym dwa największe światowe mocarstwa zaangażowane były w zimną wojnę i wyścig zbrojeń. Umiejętność znalezienia właściwych strategii politycznych w konfliktowych sytuacjach była więc wtedy szalenie ważna, rola naukowców w znajdowaniu najlepszych strategii zaś na tyle duża, że w latach 60. XX wieku dostęp do niektórych artykułów Aumanna był ograniczony!

My zacznijmy jednak od mniej poważnych tarć, a mianowicie od konfliktów małżeńskich. Wyobraźmy sobie sytuację, w której każdy z małżonków musi zdecydować, co będzie robił wieczorem. Oczywiście, przyjemność sprawić może tylko wspólne wyjście, ale mąż wolałby zobaczyć mecz piłkarski (M), a żona balet (B). Tę sytuację „wojny płci” można przedstawić za pomocą następującej macierzy wypłat:

Decyzja żony to wybór wiersza, a męża – kolumny; zadowolenie żony opisuje pierwsza, a męża – druga liczba w wybranym polu tabeli.

W tej grze mamy trzy równowagi Nasha:

• jeśli oboje małżonkowie zdecydują się pójść na balet (para strategii czystych (B, B)),
• jeśli oboje zdecydują się pójść na mecz (para strategii czystych (M,M)),
• albo jeśli każde w celu rozstrzygnięcia dylematu będzie rzucać niesymetryczną monetą (para strategii mieszanych)

W pierwszym przypadku faworyzowana jest żona, w drugim – mąż. W trzecim co prawda nikt, ale za to może się tak zdarzyć, że małżonkowie wylosują różne rozrywki i żadne z nich nie będzie szczęśliwe. Co robić?

Jeśli małżonkowie mogą porozmawiać przed podjęciem decyzji, to mogą np. ustalić, że pójdą na balet. Zauważmy, że jeśli się umówią, to nikt nie będzie miał motywacji do tego, żeby umowę jednostronnie zrywać – nawet mąż, któremu nie opłaca się zostawić żony samej przed budynkiem opery, choć jego wieczór nie będzie całkiem udany, bo oczywiście wolałby iść z żoną na mecz. Innym problemem jest to, w jaki sposób ustalić wspólny plan. Jedną z możliwości rozstrzygnięcia między wieloma równowagami jest odwołanie się np. do rzutu monetą. Rozszerzając wyjściową grę o ten dodatkowy ruch wykonywany (przez naturę), zanim którekolwiek z małżonków podejmie decyzję, rozszerzamy też de facto zbiory strategii graczy (mogą uzależnić swój wybór od tego, co zostanie wylosowane). Jeśli teraz zastanowimy się nad tym, jakie w grze są równowagi, to dochodzimy do wprowadzonego przez Aumanna [2] pojęcia równowagi skorelowanej. Równowaga ta podobna jest do równowagi Nasha w strategiach mieszanych, ale odpowiada sytuacji, w której losowe wybory graczy nie muszą być niezależne. W naszym przypadku równowagą Aumanna byłaby np. para strategii (B – jeśli orzeł, M – jeśli reszka; B – jeśli orzeł, M – jeśli reszka), niezależnie od tego, czy moneta jest symetryczna.

Jednak, niestety, nie zawsze jest tak, że nawet jeśli umowa została już zawarta, to opłaca się jej przestrzegać. Jeśli do wyboru wieczorem małżonkowie mają sprzątanie mieszkania (S) lub siedzenie na kanapie (K), to macierz wypłat mogłaby wyglądać następująco:

Każdy jest najszczęśliwszy, jeśli mieszkanie jest czyste, a prace zostały wykonane przez współmałżonka; trochę mniej szczęśliwy – jeśli prace porządkowe były wykonywane wspólnie; jeszcze mniej – jeśli mieszkanie jest brudne, ale na kanapie nie siedział w pojedynkę; i wcale – jeśli sam musiał sprzątać mieszkanie. Tym razem małżeństwo – jako całość – byłoby najszczęśliwsze, gdyby wybrana została para strategii (S,S). Jednak każdemu z małżonków z osobna opłaca się wybrać siedzenie na kanapie (strategia K jest dominująca: lepsza niezależnie od tego, czy współmałżonek wybiera S, czy K), więc jedynym możliwym wynikiem tej gry małżeńskiej, w sytuacji gdy nie można zawierać umów, jest (K,K).

Ale czy możliwość zawarcia umowy (każdy wybiera S) zagwarantowałaby porządek w mieszkaniu? Niestety, najprawdopodobniej nie: to, że umowa została zawarta, nie zmieniło faktu, że każdemu bardziej się opłaca niezgodna z umową strategia K. Zwłaszcza, jeśli współmałżonek miałby dotrzymać umowy. O ile więc nie ma zewnętrznych mechanizmów wymuszających przestrzeganie umów, to w tej sytuacji równie dobrze mogłoby umowy nie być – wynik gry pozostaje ten sam.

Powyżej mamy sytuację, w której jedna strategia (K) jest wyraźnie lepsza od tej, do której wybrania zmusza umowa (S). Jednak problem z respektowaniem umów może pojawić się również wtedy, kiedy nie zmuszamy nikogo do podejmowania decyzji „wbrew sobie”. Załóżmy scenariusz jak powyżej, z tym że teraz każdy czuje się najbardziej szczęśliwy, jeśli mieszkanie jest czyste, a prace wykonane zostały wspólnie (podczas siedzenia na kanapie i patrzenia na sprzątającego współmałżonka odczuwa się przecież wyrzuty sumienia):

Teraz znów możliwe są trzy równowagowe pary strategii: (S,S), (K,K) oraz rzucanie niesymetryczną monetą (   ).

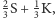
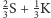Przypuśćmy, że małżonkowie umówili się, że oboje będą sprzątać (najkorzystniejsza dla wszystkich sytuacja). Jednak każde z nich może rozumować w następujący sposób:

A zatem: problem z dotrzymywaniem umowy może się pojawić także wtedy, kiedy dwie strony umawiają się na wybór korzystnej dla wszystkich kombinacji strategii, i to takich, które prowadzą do równowagi! A może jednak są jakieś warunki, w których umów opłaca się dotrzymywać?

W swoich pracach (np. [1]) Aumann zastanawiał się, między innymi, nad tym, jaki wpływ na skłonność do kooperacji będzie miał fakt, że gra między tymi samymi partnerami może być rozgrywana nie raz, lecz wiele razy; i to tak wiele, że w dowolnym momencie zostanie jeszcze „bardzo dużo” gier do rozegrania (odpowiednikiem tej sytuacji w modelu matematycznym będzie „supergra”  składająca się z nieskończenie wielu partii tej samej gry podstawowej).

Wróćmy do początkowego dylematu: mecz czy balet. Jeśli małżonkowie mają w perspektywie nie jedno wieczorne wyjście, lecz wiele, to zapewne bez problemu ustalą, że dziś wybór pada na balet, następnym razem pójdą na mecz, potem znów obejrzą balet itd. W tej sytuacji nie dość, że za każdym razem najlepiej będzie dotrzymać umowy, to jeszcze rozwiązanie wygląda sprawiedliwie.

A przy wielokrotnym wyborze między sprzątaniem a kanapą? Teraz każdy z małżonków może rozumować w ten sposób: „Umówiliśmy się, że sprzątamy. Jeśli tym razem złamię umowę, to zaufanie zostanie nadszarpnięte, i druga strona już zawsze wybierze kanapę; wiedząc to, ja też już na pewno nigdy nie zdecyduję się sprzątać. To znaczy, że już zawsze żyć będziemy w brudnym mieszkaniu. To, co ewentualnie mogę zarobić, uchylając się od umowy dziś wieczorem, stracę więc z nawiązką w przyszłości; a zatem opłaca mi się umowy dotrzymać”. Zauważmy, że to samo rozumowanie działa zarówno wtedy, kiedy para (S,S) jest równowagą pojedynczej gry, jak i wtedy, kiedy równowagą nie jest. Można udowodnić, że takie „wydłużenie horyzontu”, które w codziennym życiu może się dokonywać także np. przez zwiększenie częstotliwości interakcji, sprzyja skłonności do kooperacji.

Rozwiązaliśmy więc (częściowo przynajmniej) problem dotrzymywania umów. Jednak żeby było czego przestrzegać, umowa musi powstać. Sztuka negocjacji jest w dużej mierze domeną psychologii, ale Schelling pokazał, że i teoria gier ma tutaj coś do powiedzenia. Co zatem można zrobić, żeby polepszyć swoją sytuację podczas negocjacji umowy w przypadku konfliktu interesów?

Postawmy się w sytuacji małżonków, którzy muszą ustalić, czy wieczorem wybiorą się na Jedyny w Swoim Rodzaju Balet czy Niepowtarzalny Mecz. Deklarowanie, że „tym razem na pewno nie ustąpię”, nie podziała, gdyż druga strona wie, że jeśli zajdzie konieczność, to każdy się ugnie, bo nade wszystko nie chce zostać sam. Podpowiedź jest jednak paradoksalna: można polepszyć swoją pozycję przetargową poprzez… pogorszenie własnej sytuacji, gdyby miał nastąpić wybór innej niż postulowana strategii. Przypuśćmy, że mąż powie: „Założyłem się z kolegą, że do końca życia będę mu stawiał piwo, jeśli uda ci się namówić mnie, żebym obejrzał ten balet; mam na to niezbity dowód w postaci notarialnie potwierdzonej umowy”. Taka groźba jest wiarygodna (zadowolenie męża z ewentualnego wspólnego wieczoru w balecie zostało niezaprzeczalnie zamienione w tragedię, a strategia M stała się strategią dominującą), i żona powinna stwierdzić, że w takim razie upierać się przy balecie nie warto. Taktyka ta może być nieskuteczna jedynie w przypadku, gdyby się miało okazać, że w odpowiedzi na to żona wyciągnie dokument podobnej treści...

Przypuśćmy teraz, że mamy poważniejszy konflikt do rozwiązania: dwa kraje w trakcie wyścigu zbrojeń. Czy jeden z nich może udowodnić drugiemu poza wszelką wątpliwość, że chce uniknąć wojny? Schelling [3] argumentuje, że owszem: jeśli kraj (nawet bez umowy) wycofa się z wdrażania systemów obrony przed atakiem, daje jasny sygnał, że szkodzić drugiemu będzie tylko w ramach ewentualnej akcji odwetowej („zdolność do brania odwetu jest bardziej przydatna, niż zdolność do odpierania ataków”). Co zaś zrobić, żeby uwiarygodnić groźbę odwetu? Twierdzenie Schellinga jest następujące: odwet niepewny jest bardziej wiarygodny i efektywny niż odwet pewny. Jeśli jedno państwo upiera się przy twierdzeniu, że najbłahsza przesłanka spowoduje reakcję w postaci ataku jądrowego – jest mało wiarygodne: można przypuszczać, że ponieważ wie, do jakiej eskalacji konfliktów i zniszczeń to doprowadzi, to nie zdecyduje się na taką formę odwetu. Jeśli jednak prezydentem w kraju zostanie ktoś postrzegany przez drugą stronę jako szaleniec, który może podejmować decyzje wbrew zdrowemu rozsądkowi lub losowo (irracjonalnie, z punktu widzenia przeciwnika) – to wtedy zagrożenie odwetem staje się bardziej wiarygodne. Niektórzy uważają, że podobną strategię stosował prezydent USA Richard Nixon.

Oczywiście fakt, że Schelling i Aumann wprowadzali pewne pojęcia dopiero w drugiej połowie XX wieku, nie znaczy, że opisane mechanizmy nie były znane politykom wcześniej. Dlaczego Niemcy podczas drugiej wojny światowej nie napadły na Szwajcarię? Na pewno jednym z powodów był fakt zainstalowania przez Szwajcarów niemożliwych do wyłączenia mechanizmów destrukcji sejfów bankowych, które to mechanizmy aktywować się miały samoczynnie w przypadku wykrycia ataku. A to przecież klasyczny przypadek groźby wiarygodnej.