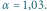Ilu mamy przodków?
Jak wiadomo, każdy człowiek ma dwoje rodziców. Skoro każdy z rodziców
też jest człowiekiem, ta rekurencyjna zależność pozwala w prosty
sposób wyznaczyć liczbę przodków dowolnej osoby w linii prostej
w kolejnych pokoleniach: czworo babć i dziadków, ośmioro prababć
i pradziadków, a zatem ogólnie
 dziadków obojga płci mamy
dziadków obojga płci mamy
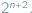

Na nieszczęście, powyższa zależność w dłuższym przedziale czasu prowadzi do paradoksu: jak bowiem możemy mieć ponad miliard przodków w trzydziestym pokoleniu, jeśli przewidywana liczba ludności świata w tym okresie (około roku 1300 n.e.) nie przekraczała 500 milionów? Aby wyjaśnić ten paradoks, wystarczy zauważyć, że w każdej ilościowo ograniczonej populacji pary zawsze tworzone są pomiędzy osobami spokrewnionymi, choćby w minimalnym stopniu. W związku z tym każdy ze wspólnych przodków tej pary będzie liczony dwukrotnie w drzewie genealogicznym każdego z jej potomków. Przy rozpatrywaniu wielu pokoleń (a więc wielkiej liczby przodków) zjawisko to zdarza się bardzo często.
Niestety, wyjaśnienie to nie zbliża nas do ilościowej odpowiedzi na zadane w tytule pytanie. Aby takiej odpowiedzi udzielić, należy dokonać pewnych założeń dotyczących przyjętego modelu populacji i dziedziczenia.
Założenia modelu
Pierwszym uproszczeniem, którego dokonamy, modelując populację, będzie podzielenie jej na pokolenia. Zakładamy, że pary czy też związki mogą być zawierane tylko przez osoby należące do tego samego pokolenia. Dzięki temu ciągłe zagadnienie modelowania liczby ludności sprowadza się do zagadnienia dyskretnego. Przyjmiemy ponadto, że tworzone pary są ściśle monogamiczne oraz niezmienne. W rozpatrywanym modelu zakładamy, że pary tworzone są w sposób losowy wewnątrz pokolenia, pomijać natomiast będziemy osoby niewchodzące w skład żadnej pary.
Dzięki przyjętym założeniom możemy za podstawową jednostkę modelu przyjąć nie pojedynczą osobę, lecz parę złożoną z dwóch osób przeciwnej płci. W tym ujęciu każda jednostka (para) pochodzi od dwóch jednostek (dwóch par rodziców) z poprzedniego pokolenia. Dzięki takiemu przedstawieniu sytuacji całkowicie unikamy problemów związanych z kategorią płci jako takiej. Od tego momentu (do odwołania) określenia „potomek” oraz „rodzic” będą dotyczyć jednostek, czyli de facto par.
„Magiczne” założenie
Dotychczasowe założenia modelu wynikały w naturalny sposób z określonych wniosków dotyczących realnego świata. Dla odmiany, ostatnie przyjęte w modelu założenie będzie jego cechą charakterystyczną. Nazywamy je „magicznym”, ponieważ mimo pozornie trywialnej treści ma znaczące konsekwencje. Oto ono:
dopasowania rodziców dla poszczególnych dzieci są od siebie niezależne.
Jak to rozumieć? Wyobraźmy sobie, że w pokoleniu dzieci wskazujemy dwie jednostki i oznaczamy je jako A i B. W tym momencie rodziców A może stanowić z równym prawdopodobieństwem każda nieuporządkowana dwójka jednostek z pokolenia rodziców. Istota założenia polega na tym, że niezależnie od wskazania rodziców dla jednostki A wybór rodziców dla jednostki B nadal jest losowy z równym prawdopodobieństwem dla każdej dwójki.
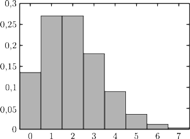
Rys. 1 Rozkład dzietności
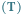 przy stałej liczebności populacji
przy stałej liczebności populacji
Okazuje się, że przy takich założeniach jedynymi parametrami modelu są
liczebności poszczególnych pokoleń. W szczególności, znając liczebność
pokolenia rodziców (
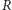 ) i liczebność pokolenia dzieci (
) i liczebność pokolenia dzieci (
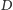 ),
można wyznaczyć strukturę dzietności, czyli rozkład zmiennej losowej
),
można wyznaczyć strukturę dzietności, czyli rozkład zmiennej losowej
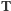 opisującej liczbę potomków wybranej jednostki z pokolenia
rodziców. Otrzymany wynik ma postać rozkładu dwumianowego z ilością
prób równą
opisującej liczbę potomków wybranej jednostki z pokolenia
rodziców. Otrzymany wynik ma postać rozkładu dwumianowego z ilością
prób równą
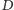 i parametrem
i parametrem
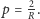 Biorąc pod uwagę, że
liczebności populacji są zwykle dość duże, dobrym przybliżeniem tego
rozkładu staje się rozkład Poissona z parametrem
Biorąc pod uwagę, że
liczebności populacji są zwykle dość duże, dobrym przybliżeniem tego
rozkładu staje się rozkład Poissona z parametrem
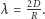 Rozkład
w szczególnym przypadku populacji o stałej liczebności (dla
Rozkład
w szczególnym przypadku populacji o stałej liczebności (dla
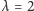 )
przedstawiony jest na wykresie.
)
przedstawiony jest na wykresie.
Funkcja przejścia
Założenia modelu mówią, że każda jednostka pochodzi od dwóch rodziców. Zastanówmy się w takim razie, od ilu rodziców pochodzą dwie jednostki? Naturalna wydaje się odpowiedź: „od czterech”, ale przecież zachodzi to tylko wtedy, gdy jednostki te nie mają wspólnych rodziców.
Rozważmy bardziej ogólną sytuację, w której spośród pokolenia dzieci
wybieramy
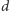 jednostek i badamy wartość
jednostek i badamy wartość
 – moc zbioru
rodziców wybranych dzieci. Rozwiązaniem tego zagadnienia dla zadanego
– moc zbioru
rodziców wybranych dzieci. Rozwiązaniem tego zagadnienia dla zadanego
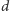 jest zmienna losowa o rozkładzie
jest zmienna losowa o rozkładzie
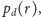 przyjmującym
niezerowe wartości jedynie dla
przyjmującym
niezerowe wartości jedynie dla
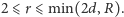
Rozkłady
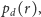 wyznaczone kombinatorycznie i zapisane w postaci
rekurencyjnej, nie wyglądają zachęcająco:
wyznaczone kombinatorycznie i zapisane w postaci
rekurencyjnej, nie wyglądają zachęcająco:
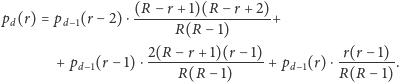 |
Jak się jednak okazuje po prostym badaniu metodami numerycznymi,
każdy z nich przyjmuje znacząco niezerowe wartości tylko w niewielkim
przedziale otaczającym maksimum. Na dodatek, szerokość tego przedziału
zmniejsza się szybko wraz ze wzrostem liczebności populacji. Wobec
tego przybliżymy poszczególne rozkłady
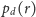 rozkładami
jednopunktowymi zlokalizowanymi w maksimach – położenia owych
maksimów oznaczmy przez
rozkładami
jednopunktowymi zlokalizowanymi w maksimach – położenia owych
maksimów oznaczmy przez
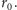 Będziemy zatem poszukiwać
wartości
Będziemy zatem poszukiwać
wartości
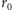 w zależności od parametru
w zależności od parametru
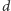 rozkładu.
Poszukiwana funkcja
rozkładu.
Poszukiwana funkcja
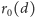 ma tutaj bardzo sensowną interpretację:
jest to oczekiwana liczba rodziców dla
ma tutaj bardzo sensowną interpretację:
jest to oczekiwana liczba rodziców dla
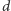 jednostek z pokolenia
dzieci.
jednostek z pokolenia
dzieci.
Wróćmy na chwilę do zmiennej losowej
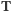 przedstawiającej
strukturę dzietności populacji. Zauważmy najpierw, że bezpośrednio
z rozkładu tej zmiennej możemy odczytać wartość
przedstawiającej
strukturę dzietności populacji. Zauważmy najpierw, że bezpośrednio
z rozkładu tej zmiennej możemy odczytać wartość
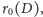 czyli
przewidywaną liczbę rodziców całego pokolenia. Wartość ta będzie
równa
czyli
przewidywaną liczbę rodziców całego pokolenia. Wartość ta będzie
równa

Następnie zauważmy, że jeśli z pokolenia dzieci wyodrębnimy
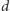 jednostek, to (na podstawie „magicznego” założenia) jakiekolwiek
przyporządkowania dokonane dla nich będą niezależne od przyporządkowań
dla pozostałych jednostek. Zatem, wynik dla
jednostek, to (na podstawie „magicznego” założenia) jakiekolwiek
przyporządkowania dokonane dla nich będą niezależne od przyporządkowań
dla pozostałych jednostek. Zatem, wynik dla
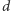 jednostek wybranych
z pokolenia o liczebności
jednostek wybranych
z pokolenia o liczebności
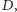 czyli
czyli
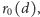 powinien być taki
sam, jak wynik dla całego pokolenia o liczebności
powinien być taki
sam, jak wynik dla całego pokolenia o liczebności
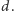 Na mocy tej
obserwacji otrzymujemy
Na mocy tej
obserwacji otrzymujemy
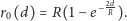 |
Można sprawdzić, że dla odpowiednio licznych populacji (
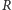 dużo
większe od
dużo
większe od
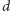 ) jest
) jest
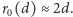
Zliczanie
Aby policzyć przodków z poszczególnych pokoleń, musimy przyjąć
określony model liczebności. Powracając do liczenia osób, a nie par,
określić należy ciąg
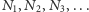 wyrażający liczebności
poszczególnych pokoleń (liczonych wstecz). Analogicznie, przez
wyrażający liczebności
poszczególnych pokoleń (liczonych wstecz). Analogicznie, przez
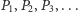 oznaczmy liczby przodków kolejnych stopni (rodziców,
dziadków, pradziadków…). Zauważmy, że dla dowolnego
oznaczmy liczby przodków kolejnych stopni (rodziców,
dziadków, pradziadków…). Zauważmy, że dla dowolnego
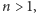 przy
rozpatrywaniu związku pomiędzy pokoleniami
przy
rozpatrywaniu związku pomiędzy pokoleniami
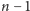 i
i
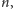 liczba par
z pokolenia dzieci równa jest
liczba par
z pokolenia dzieci równa jest
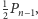 liczba zaś par rodziców
liczba zaś par rodziców
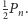 Jednocześnie, liczba wszystkich par z pokolenia rodziców, czyli
Jednocześnie, liczba wszystkich par z pokolenia rodziców, czyli
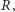 wynosi
wynosi
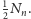 Zatem, korzystając z obliczonej poprzednio
postaci funkcji
Zatem, korzystając z obliczonej poprzednio
postaci funkcji
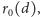 mamy
mamy
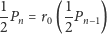 |
dla dowolnego
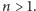
Dodatkowo, biorąc pod uwagę, że mamy dwoje rodziców (
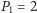 ), oraz
podstawiając do powyższego wzoru jawną postać funkcji
), oraz
podstawiając do powyższego wzoru jawną postać funkcji
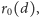 możemy
napisać następującą rekurencję:
możemy
napisać następującą rekurencję:
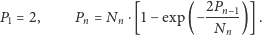 |
Jednoparametrowy model liczebności
Przyjmując prosty model liczebności opisany jednym parametrem
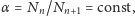 można jakościowo scharakteryzować wyniki
otrzymane przez numeryczne rozwiązanie powyższej rekurencji. Wyróżniamy
trzy fazy:
można jakościowo scharakteryzować wyniki
otrzymane przez numeryczne rozwiązanie powyższej rekurencji. Wyróżniamy
trzy fazy:
- faza wzrostu wykładniczego dla najbliższych pokoleń, w której
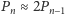 ;
;
- faza przejściowa, w której
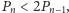 występująca
w okolicy
występująca
w okolicy
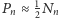 ;
;
- faza nasycenia charakteryzująca się stałym ilorazem
(współczynnikiem nasycenia)
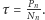
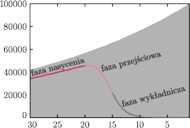
Rys. 2 Wyniki dla modelu jednoparametrowego z
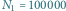 oraz
oraz
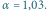
Współczynnik nasycenia w powyższym modelu można obliczyć, szukając
granicy ciągu
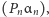 a więc rozwiązując równanie
a więc rozwiązując równanie
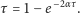 |
Przy populacji o stałej liczebności (
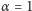 ) współczynnik ten
osiąga wartość
) współczynnik ten
osiąga wartość
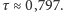 Oznacza to, że dla takiej populacji
w odległych pokoleniach przodkowie stanowią niezmiennie prawie 80% całego
pokolenia.
Oznacza to, że dla takiej populacji
w odległych pokoleniach przodkowie stanowią niezmiennie prawie 80% całego
pokolenia.
Co poza tym?
Nie da się nie zauważyć, że przedstawiony tu model obliczeń jest znacząco uproszczony. Dla rzeczywistych, dużych populacji, dobór osób w pary nie odbywa się całkowicie losowo, lecz zazwyczaj istnieje skłonność do szukania partnerów wśród bliższego otoczenia. Uzasadnione więc byłoby wyodrębnienie grup wewnątrz populacji, dopuszczając jednocześnie (z określonym prawdopodobieństwem) możliwość krzyżowania pomiędzy grupami. Ponadto, podział na pokolenia nie jest do końca naturalny, szczególnie w populacjach, w których nie obowiązują ścisłe reguły (np. kulturowe) dotyczące różnic wieku.
Bardziej złożony model, uwzględniający rzeczywiste migracje ludności i izolacje poszczególnych grup (geograficzne, językowe…), wykorzystali Rohde, Olson i Chang w swoim artykule Modelling the recent common ancestry of all living humans opublikowanym w Nature. Oszacowali oni czas pojawienia się tzw. Ostatniego Wspólnego Przodka wszystkich obecnie żyjących ludzi na Ziemi na pierwsze lub drugie tysiąclecie p.n.e. Genealodzy, do pracy!
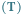 przy stałej liczebności populacji
przy stałej liczebności populacji
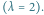
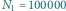 oraz
oraz