Co ciekawe, twórcy metaheurystyk w wielu przypadkach (algorytmy ewolucyjne, sieci neuronowe, systemy mrówkowe) czerpali inspirację z natury, gdyż to dla niej właśnie wydajność i łatwość dostosowania są sprawą kluczową, a prostota – częstą cechą zaproponowanych przez nią rozwiązań.

Rys. 1a) mrówki wędrują pomiędzy gniazdem a źródłem pokarmu

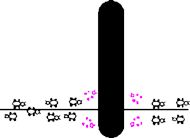
Rys. 1b) kładziemy przeszkodę; pozostały na ścieżce feromon sprawia, że mrówki z równym prawdopodobieństwem idą w obie strony

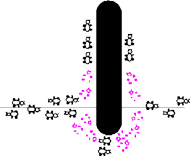
Rys. 1c) na krótszej ścieżce wkrótce pojawia się więcej feromonu

Niekiedy są to rozwiązania naprawdę niebanalnych problemów. Na przykład – jak prawie ślepe mrówki, niepotrafiące się komunikować i dysponujące mocno ograniczoną pamięcią i intelektem, mają znajdować źródła pokarmu? Przez długi czas fakt, że jednak to robią i to bardzo sprawnie (w większości przypadków znajdują nawet najkrótszą drogę pomiędzy gniazdem a pokarmem), stanowił zagadkę dla myrmekologów. Odpowiedź może być zaskakująca – zachowaniem mrówek kierują jedynie trzy proste zasady. Pierwsza – każda mrówka znaczy swoje ślady feromonem, druga – owad wybiera ścieżkę z prawdopodobieństwem proporcjonalnym do ilości feromonu na niej, trzecia – feromon z czasem stopniowo odparowuje. Dlaczego to działa? Mrówka, która znajdzie krótką drogę do pokarmu, wróci do gniazda (prawdopodobnie po własnych śladach) szybciej niż inne. Trasa, którą podążyła, będzie więc pokryta podwójną warstwą feromonu, podczas gdy inne ścieżki w okolicy gniazda otrzymały tylko pojedynczą dawkę. Spowoduje to, że wychodzące z gniazda mrówki chętniej wybiorą tę właśnie ścieżkę, co zwiększy ilość feromonu na niej, co zachęci inne owady... Odparowywanie feromonu z kolei sprawia, że mrówki nie poprzestają na znalezieniu lokalnego maksimum i umożliwia im dostosowanie się do zmian środowiska (przykład na rysunku).

Spróbujmy teraz zamienić ten sprytny pomysł Matki Natury na metaheurystykę z prawdziwego zdarzenia. Chcielibyśmy uzyskać ogólny schemat rozwiązywania szerokiej klasy problemów, zacznijmy jednak nieco skromniej – od próby rozwiązania trudnego obliczeniowo problemu komiwojażera (wybieramy akurat ten problem, gdyż wydaje się on zbliżony do oryginalnego zadania mrówek – również sprowadza się do znalezienia pewnego rodzaju najkrótszej drogi w grafie). Przedstawmy teraz schemat algorytmu znanego pod nazwą Ant Colony Optimization (ACO).

Niech 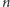będzie liczbą miast, a  – liczbą mrówek, którymi dysponujemy. Utwórzmy tablicę 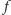o wymiarach 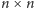reprezentującą ilość feromonu na ścieżkach pomiędzy dwoma miastami – 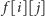oznaczać będzie ilość feromonu na ścieżce z miasta 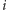do miasta 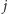(symetryczność ścieżek nie będzie nam potrzebna – równie dobrze możemy rozwiązywać asymetryczny problem komiwojażera) i zainicjujmy ją losowymi, małymi ilościami feromonu. Dalsza część algorytmu będzie się odbywała w turach, których liczbę 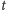zadajemy z góry w zależności od tego, jak bardzo zależy nam na szybkości uzyskania odpowiedzi. W każdej turze tworzymy podobną do tablicy 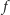tablicę 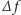, na początku tury wypełnioną zerami, reprezentującą zmiany ilości feromonu na ścieżkach zachodzące w danej turze, a następnie zaczynamy po kolei wypuszczać mrówki z miasta startowego. Każda mrówka zakreśla w grafie jakiś cykl Hamiltona, postępując następująco: będąc w 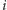 -tym mieście, przechodzi bezpośrednio do miasta 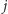-tego z prawdopodobieństwem wprost proporcjonalnym do ilości feromonu w komórce 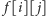i z zachowaniem warunku, że nie wolno jej powrócić do miasta, które już zdążyła odwiedzić w tej turze. Gdy mrówka kończy wędrówkę, obliczana jest długość (suma wag krawędzi) 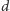przebytego przez nią cyklu, a ilość feromonu na każdej ścieżce, którą przeszła mrówka, zwiększana jest o wartość 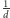(zmiany te są na razie zapisywane w tablicy ).

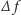Jednocześnie sprawdzamy, czy przebyty przez mrówkę cykl Hamiltona jest najlepszym z dotychczas znalezionych – w tym przypadku zapamiętujemy go. Po tym, jak wszystkie mrówki wrócą już do gniazda, do tablicy 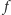dodajemy tablicę 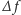, a następnie ilość feromonu w każdej komórce tablicy jest zmniejszana o 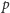procent, co reprezentuje parowanie feromonu.

Rys. 2 W Internecie można znaleźć kilka ciekawych programów służących zarówno do wizualizacji zachowania mrówek szukających pokarmu, jak też rozwiązujących problem komiwojażera. Ten zrzut ekranu pochodzi z programu AntSim.

Takie postępowanie promuje ścieżki wchodzące w skład wielu dość dobrych cykli Hamiltona, lecz pozwala się też wyróżnić ścieżce używanej rzadko, ale za to w wyjątkowo krótkich cyklach, co wydaje się rozsądne i zbliżone do rzeczywistego zachowania mrówek. Nie oznacza to jednak, że tego algorytmu nie można już udoskonalić – nasze elektroniczne mrówki nie muszą wszakże podlegać ograniczeniom nałożonym przez naturę na ich biologiczne krewniaczki. W szczególności nie muszą być ślepe – w praktycznych zastosowaniach ACO mrówki w wyborze ścieżek kierują się nie tylko ilością feromonu na nich, ale też ich długością. Najczęściej używanym wzorem na prawdopodobieństwo wyboru ścieżki. z miasta do nieodwiedzonego wcześniej miasta 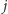jest

gdzie 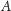 jest zbiorem miast jeszcze nieodwiedzonych, 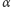i 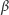 są pewnymi parametrami, a 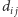jest odległością miasta 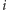od miasta 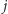(badania empiryczne wykazały, że algorytm osiąga najlepsze wyniki z 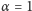 , , 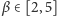współczynnikiem parowania 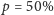i liczbą mrówek 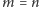). Dodatkowo nasze mrówki mogą się komunikować i zapamiętywać najlepsze do tej pory znalezione cykle – częstym udoskonaleniem algorytmu jest zwiększanie w każdej turze ilości feromonu na najlepszym cyklu, nawet jeśli w danej turze wybrało go niewiele mrówek. Poza tym elektronicznym owadom niepotrzebne jest gniazdo – mrówki nie muszą startować wszystkie z jednego miasta, mogą być rozmieszczone losowo, co daje lepsze wyniki. Tak udoskonalony algorytm może już śmiało konkurować z innymi metaheurystykami. Testy wykazały, że dla dużych ACO średnio osiąga lepsze wyniki niż najczęściej stosowane heurystyki – tzw. 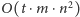symulowane wyżarzanie i algorytm ewolucyjny, a poza tym szybciej (mimo dość dużej złożoności ) znajduje dość dobre rozwiązania. Dużą zaletą jest też łatwość implementacji (w języku C++ ten algorytm można zakodować w kilkunastu linijkach). Jednym z nielicznych minusów tego podejścia jest dość duże wykorzystanie dodatkowej pamięci (potrzebujemy jej ).

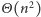ACO, jako prawdziwa metaheurystyka, może być stosowana do bardzo różnorodnych zadań. Wydaje się, że można ją przystosować do rozwiązywania bardzo wielu problemów optymalizacyjnych – wystarczy, by każde rozwiązanie naszego problemu dało się podzielić na fragmenty, lokalne „atomowe” decyzje, które razem wyznaczają rozwiązanie i które są od siebie możliwie niezależne (oczywiście, zależy nam na tym, by przestrzeń tych decyzji była możliwie mała). Potem już tylko na przestrzeni rozwiązań ustalamy funkcję celu, określającą jakość rozwiązania i ewentualnie opracowujemy jakąś pomocniczą heurystykę ułatwiającą podejmowanie lokalnych decyzji (w przypadku problemu komiwojażera była to odwrotność odległości pomiędzy miastami) – i dalszym rozwiązywaniem zadania możemy obarczyć mrówki w dobrze już nam znany sposób (wszystkie opcje, które mrówka będzie mogła wybrać w poszczególnych decyzjach, otrzymają własne zbiorniczki z feromonem, który będzie do nich dolewany po zakończeniu tury proporcjonalnie do jakości rozwiązań, w których uczestniczyły; pełniejsze zbiorniczki będą bardziej kuszące dla mrówek; feromon będzie z czasem odparowywał ze zbiorniczków). W praktyce mrówki są wykorzystywane w sterowaniu ruchem w sieciach komputerowych, w kolorowaniu grafów i znajdowaniu skojarzeń.