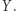Zabawa zapałkami
Jeśli czytasz ten tekst, to świetnie się składa, możesz poznać drobny fragment topologii i zmierzyć się z następującym pytaniem: Ile topologicznie różnych figur można ułożyć na płaszczyźnie z sześciu zapałek, które stykają się tylko końcami?
Dlaczego mówimy o topologicznej, a nie geometrycznej równości figur? Powód jest dość oczywisty, w geometrii euklidesowej dwie figury uznajemy za równe, gdy istnieje ruch sztywny, który przenosi jedną z nich na drugą. Z tego punktu widzenia w geometrii ilość różnych figur jest tak ogromna, że nikt nawet nie rozważa pomysłu ich katalogowania. Topologia (w odróżnieniu od bardzo bogatej w szczegóły geometrii) uwydatnia najistotniejsze cechy figur, zapominając o reszcie.
Rys. 1

Rys. 2
Figury  i
i 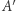 nazywamy topologicznie równymi (homeomorficznymi), gdy istnieje wzajemnie jednoznaczne przekształcenie
nazywamy topologicznie równymi (homeomorficznymi), gdy istnieje wzajemnie jednoznaczne przekształcenie 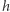 figury
figury 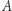 na figurę
na figurę  takie, że przekształcenia
takie, że przekształcenia 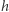 i do niego odwrotne
i do niego odwrotne  są ciągłe. Przekształcenie
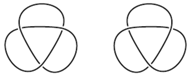
są ciągłe. Przekształcenie  o tych własnościach nazywamy homeomorfizmem. Mówiąc obrazowo, homeomorfizm to przekształcenie jednej figury na drugą, które nic nie rozrywa, nic nie skleja i dba o to, by bliskie punkty jednej figury przeprowadzić na bliskie punkty drugiej figury. Ale uwaga, nie oznacza to, że zawsze można fizycznie przekształcić jedną figurę na drugą, deformując ją stopniowo w sposób ciągły i różnowartościowy. Węzeł trójlistnik (są dwa, lewo- i prawoskrętny, Rys. 1) i okrąg są homeomorficzne, ale w przestrzeni trójwymiarowej bez użycia chirurgii (rozcinania i sklejania), przez żadne wyginanie, ściskanie, rozciąganie nie można zrobić jednego z drugiego. Banalna jest obserwacja, że okrąg i brzeg trójkąta są figurami homeomorficznymi. Gdy umieścimy brzeg trójkąta w obszarze ograniczonym okręgiem, to projekcja radialna jest homeomorfizmem przeprowadzającym jedną z tych figur na drugą (Rys. 2). Podobnie nierozróżnialne z topologicznego punktu widzenia są litery E, F, T, Y.
o tych własnościach nazywamy homeomorfizmem. Mówiąc obrazowo, homeomorfizm to przekształcenie jednej figury na drugą, które nic nie rozrywa, nic nie skleja i dba o to, by bliskie punkty jednej figury przeprowadzić na bliskie punkty drugiej figury. Ale uwaga, nie oznacza to, że zawsze można fizycznie przekształcić jedną figurę na drugą, deformując ją stopniowo w sposób ciągły i różnowartościowy. Węzeł trójlistnik (są dwa, lewo- i prawoskrętny, Rys. 1) i okrąg są homeomorficzne, ale w przestrzeni trójwymiarowej bez użycia chirurgii (rozcinania i sklejania), przez żadne wyginanie, ściskanie, rozciąganie nie można zrobić jednego z drugiego. Banalna jest obserwacja, że okrąg i brzeg trójkąta są figurami homeomorficznymi. Gdy umieścimy brzeg trójkąta w obszarze ograniczonym okręgiem, to projekcja radialna jest homeomorfizmem przeprowadzającym jedną z tych figur na drugą (Rys. 2). Podobnie nierozróżnialne z topologicznego punktu widzenia są litery E, F, T, Y.
Wykazanie topologicznej równości dwóch figur zawsze wymaga wskazania między nimi homeomorfizmu. A jak wykazać, że figury nie są homeomorficzne? Wystarczy podać własność, która nie zmienia się przy homeomorfizmach i przysługuje jednej z nich, a nie przysługuje drugiej. Skoro przekształcenia homeomorficzne nie pozwalają na rozrywanie figury ani na jej sklejanie, to najprostszymi niezmiennikami homeomorfizmów są:
- 1.
- liczba kawałków (= maksymalnych części spójnych), z których składa się figura;
- 2.
- ilość punktów rozdzielających figury, tj. ilość takich punktów figury, których usunięcie z figury powoduje jej rozpad na rozłączne kawałki;
- 3.
- indeksy punktów, tj. liczba łuków, które schodzą się w danym punkcie.

Rys. 3
Ponieważ w badaniu niehomeomorficzności figur nie wszystkie niezmienniki są tak samo skuteczne, więc bardzo pożądana jest znajomość wielu różnych niezmienników homeomorfizmów, im więcej, tym lepiej. Zobaczmy na przykładach, jak to działa. Figury z rysunku 3 są homeomorficzne (są topologicznie równe).
Gdy poszukujemy przekształcenia homeomorficznego między tymi figurami na płaszczyźnie, to... niczego takiego nie widać. Sytuacja zmienia się diametralnie, gdy te układy zapałek wyobrazimy sobie w przestrzeni trójwymiarowej i potraktujemy je jak elastyczną strukturę. Wówczas przekształcenie w przestrzeni trójwymiarowej polegające na "wywróceniu figury na drugą stronę przez wnętrze kwadratu" (lub przy nieruchomym kwadracie obrót "ogonka" w płaszczyźnie prostopadłej do płaszczyzny kwadratu) jest homeomorfizmem, który przeprowadza jedną figurę na drugą.
Tak działa wymiar, w przestrzeniach o wyższym wymiarze można wykonać operacje, które w niższych wymiarach nie istnieją i na niższe wymiary nie mają żadnego wpływu. Teraz wyobraź sobie, że trójlistnik (Rys. 1), i każdy inny węzeł, który da się zrobić z prawdziwego sznurka, można w przestrzeni czterowymiarowej rozplątać, otrzymując okrąg, oczywiście nigdzie niczego nie rozrywając. Wystarczy, korzystając z czwartego wymiaru, łuk węzła, który jest pod spodem, przenieść na wierzch lub odwrotnie (szczegóły na końcu artykułu). W przestrzeni czterowymiarowej piłkę można wywrócić na drugą stronę, nigdzie jej nie rozrywając. Prostą analogią tej sytuacji jest przekształcenie płaskiego pierścienia. Gdy dodamy trzeci wymiar, to pierścień ten tak możemy wywrócić, by jego brzeg wewnętrzny stał się brzegiem zewnętrznym. Przekształcenia te są oczywiście homeomorfizmami.

Rys. 4
Z drugiej strony, figury z rysunku 4 nie są homeomorficzne. Jedna z nich ma jeden punkt o indeksie 4, a druga takiego punktu nie ma.
Rys. 5
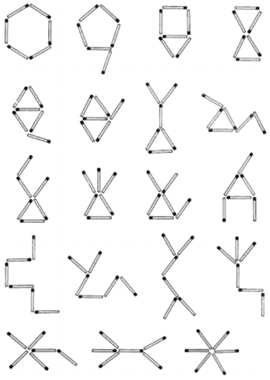
Analizując w ten sposób figury, jakie możemy utworzyć z nie więcej niż pięciu zapałek, otrzymujemy zbiory topologicznie różnych figur (Rys. 5). Naturalne jest pytanie: skąd mamy pewność, że są to wszystkie możliwe topologicznie różne figury? Warto nad tym pomyśleć. Proszę również spróbować rozwiązać postawiony problem i znaleźć wszystkie topologicznie różne figury, jakie można tak utworzyć z sześciu zapałek. Aby nie psuć zabawy, rozwiązanie podajemy tutaj. Powiemy jednak, że na płaszczyźnie z sześciu zapałek stykających się tylko końcami można utworzyć 19 topologicznie różnych figur. Jeśli ten sam problem rozpatrzymy w przestrzeni i nie ograniczymy się jedynie do płaszczyzny, to możliwa jest tylko jedna dodatkowa konfiguracja: szkielet czworościanu. Z kolei dla siedmiu zapałek można w ten sposób utworzyć na płaszczyźnie aż 39 topologicznie różnych figur.
Budując tego typu atlasy (katalogi), porządkujemy naszą wiedzę o świecie: w postaci tablicy Mendelejewa, systematyki roślin, systematyki zwierząt itp. Jednym z podstawowych zadań topologii jest klasyfikacja różnych zbiorów: węzłów, powierzchni, rozmaitości. Topologowie chcieliby z rozmaitościami dokonać tego, czego wcześniej dokonali dla powierzchni i węzłów:
- rozstrzygnąć, kiedy dwie rozmaitości są topologicznie równe,
- sklasyfikować wszystkie możliwe rozmaitości,
- znaleźć wszystkie sposoby zanurzania jednej rozmaitości w drugiej,
- rozstrzygnąć, kiedy dwa sposoby zanurzania jednej rozmaitości w drugiej są lub nie są takie same.
Ta trudna tematyka inspiruje nowe badania przyrody (i sama jest nimi inspirowana), np. w zakresie fizyki kwantowej, biologii molekularnej, teorii chaosu, ale to temat na inny artykuł.

Jak homeomorficznie przekształcić trójlistnik  na okrąg?
na okrąg?
Rozumowanie geometryczne
Węzeł  zanurzamy w przestrzeni
zanurzamy w przestrzeni 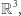 a tę w przestrzeni
a tę w przestrzeni 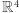 (Rys. 7). Wybieramy punkt
(Rys. 7). Wybieramy punkt 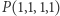 nieleżący w przestrzeni
nieleżący w przestrzeni 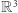 i łączymy punkt
i łączymy punkt 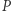 z każdym punktem węzła
z każdym punktem węzła 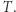 Otrzymujemy w ten sposób "stożek", którego podstawa jest w przestrzeni
Otrzymujemy w ten sposób "stożek", którego podstawa jest w przestrzeni  a jego powierzchnia boczna nie ma nic wspólnego z przestrzenią
a jego powierzchnia boczna nie ma nic wspólnego z przestrzenią 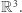 Chcemy łuk
Chcemy łuk 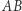 poprowadzić nad krzyżującą się z nim linią, wzdłuż linii przerywanej. Punkty łuku
poprowadzić nad krzyżującą się z nim linią, wzdłuż linii przerywanej. Punkty łuku 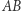 łączymy z punktem
łączymy z punktem 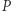 leżącym w czwartym wymiarze i po powierzchni tak utworzonego stożka, która z przestrzenią
leżącym w czwartym wymiarze i po powierzchni tak utworzonego stożka, która z przestrzenią 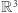 nie ma nic wspólnego, przekładamy łuk
nie ma nic wspólnego, przekładamy łuk 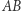 narysowany linią ciągłą na łuk
narysowany linią ciągłą na łuk 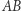 narysowany linią przerywaną. Ponieważ wszystko dzieje się poza przestrzenią
narysowany linią przerywaną. Ponieważ wszystko dzieje się poza przestrzenią 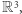 więc podczas tej operacji łuk
więc podczas tej operacji łuk 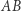 narysowany linią ciągłą w żadnym momencie nie przecina krzyżującej się z nim linii. Po usunięciu w ten sposób jednego "skrzyżowania" z figury
narysowany linią ciągłą w żadnym momencie nie przecina krzyżującej się z nim linii. Po usunięciu w ten sposób jednego "skrzyżowania" z figury 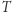 otrzymujemy krzywą zamkniętą w oczywisty sposób homeomorficzną z okręgiem.
otrzymujemy krzywą zamkniętą w oczywisty sposób homeomorficzną z okręgiem.
Rozumowanie analityczne, dla "niedowiarków"
Rozważmy przestrzeń euklidesową 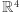 i niech
i niech 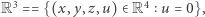
 Ponadto niech oś
Ponadto niech oś  będzie zbiorem
będzie zbiorem  (Rys. 8).
(Rys. 8).

Rozważmy łuk  Pokażemy, jak przeprowadzić łuk
Pokażemy, jak przeprowadzić łuk 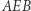 na łuk
na łuk 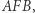 nie przecinając osi
nie przecinając osi  w przestrzeni
w przestrzeni 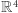 i nie ruszając z miejsca punktów
i nie ruszając z miejsca punktów  i
i 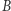 (rzecz jasna w przestrzeni
(rzecz jasna w przestrzeni  jest to niemożliwe). Oczywiście tego typu operacje pozwolą na rozplątanie trójlistnika.
jest to niemożliwe). Oczywiście tego typu operacje pozwolą na rozplątanie trójlistnika.
Etap I. Definiujemy ciągłą rodzinę ciągłych przekształceń
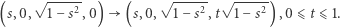 |
Wszystkie punkty łuku  poza jego końcami, "ciągniemy" w głąb przestrzeni
poza jego końcami, "ciągniemy" w głąb przestrzeni 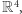 bo dla tych punktów mamy
bo dla tych punktów mamy 
Etap II. Definiujemy drugą ciągłą rodzinę ciągłych przekształceń
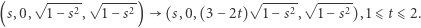 |
Efektem tych przekształceń jest "spadek" łuku wzdłuż kierunku 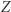 do łuku (dla
do łuku (dla 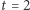 ):
):
 |
bez przecięcia osi 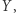 gdyż współrzędne
gdyż współrzędne 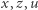 nigdy się nie zerują w tym samym czasie dla
nigdy się nie zerują w tym samym czasie dla ![| t∈ [1,2].](/math/temat/matematyka/topologia/2020/01/28/zabawa-zapalkami/7x-795ecd6bc3e09a817042128dc972eb494240f6ff-im-33,33,33-FF,FF,FF.gif)
Etap III. Opuszczamy łuk "z głębi" przestrzeni 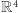 wzdłuż
wzdłuż 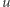 w kierunku do łuku
w kierunku do łuku  stosując ciągłą deformację
stosując ciągłą deformację
 |
Dla 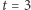 otrzymujemy łuk
otrzymujemy łuk 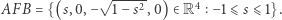 Ponieważ w czasie
Ponieważ w czasie 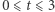 żaden punkt rozważanych łuków nie ma współrzędnych postaci
żaden punkt rozważanych łuków nie ma współrzędnych postaci 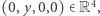 więc podczas tej deformacji następuje ciągłe przekształcenie łuku
więc podczas tej deformacji następuje ciągłe przekształcenie łuku 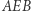 na łuk
na łuk 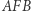 bez przecięcia osi
bez przecięcia osi