Homeomorfizm

Homeomorfizmy to przekształcenia zachowujące różne własności zbiorów (obiektów geometrycznych). Znaczy to, że pewne cechy obiektu są zachowywane przy "ściskaniu" lub "rozciąganiu", bez sklejania lub rozcinania, dziurawienia itp.

Kulę (np. zrobioną z plasteliny) można w ten sposób przekształcić w sześcian, więc kula i sześcian są homeomorficzne. Kula nie jest homeomorficzna z trójkątem (bo jest za chudy) ani preclem. Za to precel jest homeomorficzny z kubkiem:

Zbiór liczb niewymiernych (ze zwykłą metryką 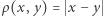$ρ(x, y) = x− y$ ) i zbiór wszystkich liczb rzeczywistych nie są homeomorficzne. Prosta to jeden "kawałek", bez żadnych dziur, w odróżnieniu od dziurawego zbioru liczb niewymiernych. Formalnie: funkcja ciągła określona na zbiorze liczb rzeczywistych, przyjmująca wartość 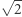$-- √ 2$ i wartość 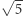$-- |√ 5$ musi też przyjąć wartość 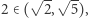$√--√ -- 2 ∈ ( 2, 5),$ która liczbą niewymierną nie jest.

Również zbiór liczb wymiernych i zbiór liczb niewymiernych nie są homeomorficzne choć oba mają nieskończenie wiele "dziur" - nie są równoliczne.

Zadanie. Przyjmijmy, że kształty obok są wykonane z dowolnie ściśliwej plasteliny. Należy znaleźć takie jej rozciąganie i ściskanie (bez rozcinania i sklejania ani zaklejania otworów), które z jednego kształtu pozwoli otrzymać drugi.

Odpowiedź można znaleźć w artykule Zabawy z plasteliną.