Twierdzenie o naszyjniku
Uczciwi złodzieje powinni umieć się dzielić. Oczywiście, dzielić się łupami z innymi uczciwymi złodziejami, którzy pomagali w dokonaniu kradzieży. Można sobie wyobrazić, że taka uczciwość powoduje czasem pewne trudności, gdyż niektóre precjoza mogą być nieskore do podziału. Dla przykładu...
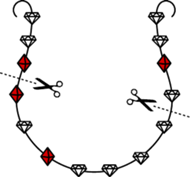
Rys. 1
...wyobraźmy sobie, że dwoje uczciwych złodziei (powiedzmy, Bonnie i Clyde) skradło naszyjnik wysadzany diamentami i rubinami i chcą między sobą po równo rozdzielić zawarte w nim szlachetne kamienie. Oczywiście, aby to było możliwe, liczba diamentów oraz liczba rubinów na naszyjniku muszą być parzyste. Załóżmy dodatkowo, że złodzieje - ceniący sztukę i misterną konstrukcję naszyjnika - chcą go przeciąć w jak najmniejszej liczbie miejsc, tak aby powstałe w ten sposób fragmenty mogli między siebie rozdzielić w sposób sprawiedliwy względem liczby diamentów oraz rubinów (zapięcie naszyjnika nie musi być zamknięte). Rysunek 1 pokazuje sposób podziału naszyjnika z 10 diamentami i 4 rubinami przy użyciu dwóch cięć w taki sposób, by każdy złodziej otrzymał 5 diamentów i 2 rubiny. Oczywiście, mniejsza liczba cięć nie jest możliwa. Może jednak istnieje inny diamentowo-rubinowy naszyjnik, którego nie da się sprawiedliwie podzielić przy użyciu dwóch cięć? Okazuje się, że nie, co nietrudno jest udowodnić.
Rozważmy naszyjnik z 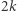 diamentami i
diamentami i 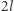 rubinami. Dla
rubinami. Dla 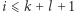 rozważmy podział
rozważmy podział 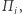 w którym kamienie o numerach
w którym kamienie o numerach 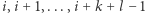 przygarnia Bonnie, a pozostałe Clyde. Oczywiście, każdy taki podział jest możliwy do zrealizowania przy użyciu dwóch cięć. Załóżmy, że przy podziale
przygarnia Bonnie, a pozostałe Clyde. Oczywiście, każdy taki podział jest możliwy do zrealizowania przy użyciu dwóch cięć. Załóżmy, że przy podziale 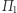 Bonnie dostał
Bonnie dostał 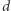 diamentów i bez straty ogólności przyjmijmy
diamentów i bez straty ogólności przyjmijmy 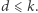 Wówczas Clyde musi mieć
Wówczas Clyde musi mieć 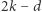 diamentów, zatem tyle samo ma Bonnie przy podziale
diamentów, zatem tyle samo ma Bonnie przy podziale 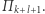 Ponadto, gdy zmieniamy podział z
Ponadto, gdy zmieniamy podział z 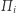 na
na 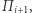 liczba diamentów przyznanych Bonniemu zmienia się o co najwyżej 1. W tej sytuacji, zmieniając się od
liczba diamentów przyznanych Bonniemu zmienia się o co najwyżej 1. W tej sytuacji, zmieniając się od 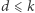 (przy
(przy 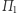 ) do
) do 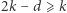 (przy
(przy 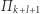 ), liczba diamentów w posiadaniu Bonniego przy pewnym podziale będzie musiała wynosić
), liczba diamentów w posiadaniu Bonniego przy pewnym podziale będzie musiała wynosić 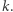 Oczywiście, wówczas będzie on mieć
Oczywiście, wówczas będzie on mieć 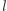 rubinów (gdyż zawsze otrzymuje
rubinów (gdyż zawsze otrzymuje 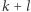 kamieni), a zatem uzasadniliśmy istnienie sprawiedliwego podziału uzyskiwanego przy użyciu dwóch cięć.
kamieni), a zatem uzasadniliśmy istnienie sprawiedliwego podziału uzyskiwanego przy użyciu dwóch cięć.
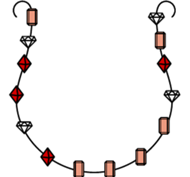
Rys. 2 Zachęcam Czytelnika do próby samodzielnego znalezienia sprawiedliwego podziału na 4 części, a także uzasadnienia, że 3 części to za mało.
Powstaje naturalne pytanie: co mogą zrobić złodzieje, jeśli rodzajów kamieni jest więcej? Rysunek 2 przedstawia naszyjnik wysadzany diamentami, rubinami i szmaragdami, którego nie da się sprawiedliwie podzielić, używając dwóch cięć, choć jest to możliwe przy użyciu trzech cięć. Czy zatem w przypadku 3 rodzajów kamieni zawsze wystarczą 3 cięcia? A jeśli tak, to czy przy naszyjniku z 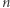 różnymi rodzajami kamieni zawsze możemy wykonać tylko
różnymi rodzajami kamieni zawsze możemy wykonać tylko  cięć, aby uzyskać sprawiedliwy podział? Twierdzącej odpowiedzi na to pytanie udzielili Noga Alon i Douglas West (The Borsuk-Ulam theorem and bisection of necklaces, Proceedings of the American Mathematical Society, 1986). Przedstawione przez nich rozumowanie jest niezwykle piękne, między innymi dlatego, że opiera się natwierdzeniu Borsuka-Ulama, kojarzonym z topologią, a nie z problemami natury tak dyskretnej, jak podział łupów. Twierdzenie to brzmi następująco.
cięć, aby uzyskać sprawiedliwy podział? Twierdzącej odpowiedzi na to pytanie udzielili Noga Alon i Douglas West (The Borsuk-Ulam theorem and bisection of necklaces, Proceedings of the American Mathematical Society, 1986). Przedstawione przez nich rozumowanie jest niezwykle piękne, między innymi dlatego, że opiera się natwierdzeniu Borsuka-Ulama, kojarzonym z topologią, a nie z problemami natury tak dyskretnej, jak podział łupów. Twierdzenie to brzmi następująco.
Twierdzenie. Niech 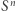 będzie
będzie 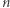 -wymiarową sferą jednostkową, tzn.
-wymiarową sferą jednostkową, tzn.

i niech 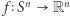 będzie dowolną funkcją ciągłą. Wówczas istnieje punkt
będzie dowolną funkcją ciągłą. Wówczas istnieje punkt 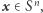 dla którego
dla którego 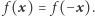
Więcej o twierdzeniu Borsuka-Ulama można przeczytać w artykule Michała Miśkiewicza w Delcie 09/2018.
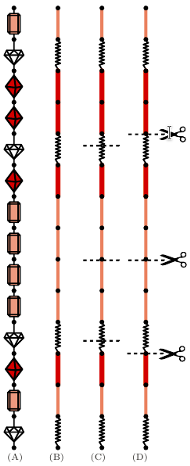
(A) rozłożony naszyjnik,
(B) "rozsmarowanie" kamieni,
(C) podział naszyjnika wynikający z twierdzenia Borsuka-Ulama,
(D) poprawka poprzedniego podziału, aby cięcia wypadły w zaznaczonych punktach
Przyjrzyjmy się, jak przedstawiony wynik "pracuje" w rozważanym zagadnieniu. Dla uproszczenia przyjmijmy, że mamy do czynienia z trzema rodzajami kamieni, dowód w ogólnym przypadku jest w pełni analogiczny. Rozważmy naszyjnik z 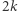 diamentami,
diamentami, 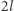 rubinami i
rubinami i 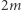 szmaragdami. Załóżmy, że naszyjnik ma długość
szmaragdami. Załóżmy, że naszyjnik ma długość 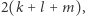 a po jego rozprostowaniu
a po jego rozprostowaniu 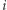 -ty kamień znajduje się w odległości
-ty kamień znajduje się w odległości 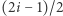 od górnego zapięcia. Dla ułatwienia opisu niech
od górnego zapięcia. Dla ułatwienia opisu niech 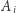 będzie punktem na naszyjniku w odległości
będzie punktem na naszyjniku w odległości 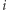 od górnego zapięcia (tzn.
od górnego zapięcia (tzn. 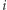 -ty kamień znajduje się w środku odcinka
-ty kamień znajduje się w środku odcinka 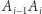 ).
).
Wyobraźmy sobie, że dla każdego 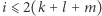 "rozsmarowujemy"
"rozsmarowujemy" 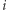 -ty kamień równomiernie po całym odcinku
-ty kamień równomiernie po całym odcinku 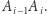 Dopuszczamy w ten sposób niecałkowitoliczbowe podziały naszych skarbów (tzn. można, na przykład, przeciąć diamentowy odcinek w połowie). Zastanówmy się, w jaki sposób można matematycznie opisać podział tego naszyjnika na cztery części, rozdzielone między dwóch złodziei. Po pierwsze, musimy określić punkty cięcia. Są one jednoznacznie wyznaczone przez długości kolejnych fragmentów naszyjnika, czyli cztery dodatnie liczby rzeczywiste, sumujące się do
Dopuszczamy w ten sposób niecałkowitoliczbowe podziały naszych skarbów (tzn. można, na przykład, przeciąć diamentowy odcinek w połowie). Zastanówmy się, w jaki sposób można matematycznie opisać podział tego naszyjnika na cztery części, rozdzielone między dwóch złodziei. Po pierwsze, musimy określić punkty cięcia. Są one jednoznacznie wyznaczone przez długości kolejnych fragmentów naszyjnika, czyli cztery dodatnie liczby rzeczywiste, sumujące się do  Dla wygody podzielmy je przez
Dla wygody podzielmy je przez 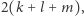 otrzymując dodatnie liczby
otrzymując dodatnie liczby 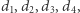 sumujące się do 1. Następnie musimy rozdzielić tak otrzymane części między złodziei. W tym celu każdej części możemy przyporządkować liczbę
sumujące się do 1. Następnie musimy rozdzielić tak otrzymane części między złodziei. W tym celu każdej części możemy przyporządkować liczbę 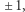 w zależności od tego, któremu rabusiowi chcemy ją wręczyć (powiedzmy, 1 dla Bonniego i
w zależności od tego, któremu rabusiowi chcemy ją wręczyć (powiedzmy, 1 dla Bonniego i 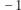 dla Clyde). Niech
dla Clyde). Niech 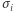 będzie znakiem przynależności
będzie znakiem przynależności 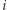 -tej części. Wówczas czwórka
-tej części. Wówczas czwórka 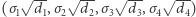 jest punktem na sferze
jest punktem na sferze 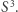 Z drugiej strony, każdy punkt
Z drugiej strony, każdy punkt 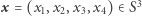 definiuje podział naszyjnika poprzez wzięcie
definiuje podział naszyjnika poprzez wzięcie 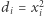 oraz
oraz 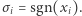
Widzimy już, że twierdzenie Borsuka-Ulama ma coraz większą szansę okazać się pomocne. Aby z niego skorzystać, musimy jeszcze określić funkcję ciągłą z 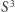 w
w 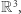 w jakiś sposób związaną z naszym podziałem łupów. Naturalnym kandydatem jest funkcja
w jakiś sposób związaną z naszym podziałem łupów. Naturalnym kandydatem jest funkcja 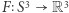 określona "wzorem"
określona "wzorem"
 |
Rozważana funkcja jest ciągła dzięki temu, że "rozsmarowaliśmy" wcześniej nasze kamienie. Na mocy twierdzenia Borsuka-Ulama istnieje zatem 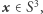 dla którego
dla którego 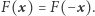 Zauważmy jednak, że
Zauważmy jednak, że 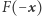 określa sumy odpowiednich fragmentów przynależnych Clyde przy podziale zdefiniowanym przez
określa sumy odpowiednich fragmentów przynależnych Clyde przy podziale zdefiniowanym przez  Istnieje zatem podział naszyjnika przy użyciu trzech cięć w taki sposób, że każde ze złodziei otrzyma taką samą sumaryczną długość fragmentów poszczególnych rodzajów.
Istnieje zatem podział naszyjnika przy użyciu trzech cięć w taki sposób, że każde ze złodziei otrzyma taką samą sumaryczną długość fragmentów poszczególnych rodzajów.
Pozostaje nam teraz wrócić z "uciąglonej" wersji problemu do twardej rzeczywistości diamentów twardych jak diamenty, niemożliwych do "rozsmarowywania" na naszyjniku. Aby zakończyć dowód, wystarczy uzasadnić, że otrzymane w poprzednim akapicie punkty cięcia możemy przesunąć (nie zmieniając sprawiedliwości podziału) tak, aby wypadły w punktach 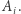 Nie jest to jednak trudne. Rozważmy wszystkie punkty cięcia, które wypadły wewnątrz pewnego diamentowego odcinka o końcach w kolejnych punktach
Nie jest to jednak trudne. Rozważmy wszystkie punkty cięcia, które wypadły wewnątrz pewnego diamentowego odcinka o końcach w kolejnych punktach 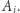 Jeśli fragmenty po obu stronach cięcia należą do jednego złodzieja, to, oczywiście, bez uszczerbku sprawiedliwości możemy przesunąć cięcie do najbliższego punktu
Jeśli fragmenty po obu stronach cięcia należą do jednego złodzieja, to, oczywiście, bez uszczerbku sprawiedliwości możemy przesunąć cięcie do najbliższego punktu 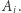 Wszystkie pozostałe spośród rozważanych punktów cięcia przesuńmy "na korzyść" Bonniego. Wówczas Bonnie zyska "diamentową" długość będącą pewną liczbą całkowitą
Wszystkie pozostałe spośród rozważanych punktów cięcia przesuńmy "na korzyść" Bonniego. Wówczas Bonnie zyska "diamentową" długość będącą pewną liczbą całkowitą 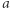 (gdyż suma "ułamkowych" diamentowych fragmentów Clyde musiała być całkowita). Wystarczy zatem, że Bonnie odda teraz
(gdyż suma "ułamkowych" diamentowych fragmentów Clyde musiała być całkowita). Wystarczy zatem, że Bonnie odda teraz  diamentów poprzez odpowiednie przesunięcie o 1 pewnych
diamentów poprzez odpowiednie przesunięcie o 1 pewnych 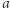 punktów cięcia. To samo można zrobić dla pozostałych rodzajów kamieni, otrzymując w ten sposób "dyskretny", sprawiedliwy podział naszyjnika.
punktów cięcia. To samo można zrobić dla pozostałych rodzajów kamieni, otrzymując w ten sposób "dyskretny", sprawiedliwy podział naszyjnika.
Kolejnym rozszerzeniem naszyjnikowej zagwozdki jest wzięcie pod uwagę większej liczby złodziei. Jaka jest zatem najmniejsza możliwa liczba cięć potrzebnych do podziału naszyjnika z 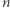 rodzajami kamieni między
rodzajami kamieni między 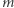 złodziei (zakładając, że jest to możliwe)? Odpowiedź jest znana, zachęcam jednak Czytelnika do próby samodzielnego sformułowania hipotezy na ten temat.
złodziei (zakładając, że jest to możliwe)? Odpowiedź jest znana, zachęcam jednak Czytelnika do próby samodzielnego sformułowania hipotezy na ten temat.