Mała Delta
Czwarty wymiar – zobaczmy
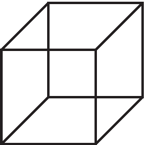
Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.
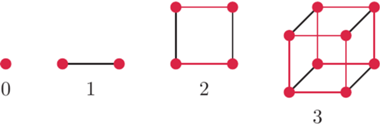
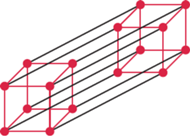
Obrazek 1 to dwa obrazki 0 połączone krawędzią. Obrazek 2 to dwie kopie 1 odpowiednio połączone krawędziami. Obrazek 3 to dwie kopie 2 również z dodanymi krawędziami. Czyli obrazek 4 powinien wyglądać tak jak obok. A teraz zastanówmy się, co to właściwie jest: 0 to zerowymiarowa kostka (punkt, nie ma wysokości, szerokości, żadnego wymiaru), 1 to jednowymiarowa kostka (odcinek - ma długość), 2 to dwuwymiarowa kostka (kwadrat - szerokość i wysokość), 3 to trójwymiarowa kostka (sześcian). Rysunek z lewej strony to kostka czterowymiarowa - tesserakt.
Co można powiedzieć o liczbie wierzchołków tesseraktu? Na rysunkach widzimy najpierw 1, potem 2, 4, 8, ... To sugeruje, że na kolejnym powinno być 16 wierzchołków (uff... zgadza się). Ile krawędzi powinno spotkać się w jednym wierzchołku? 0 w kostce 0-wymiarowej, 1 w kostce 1-wymiarowej, 2 w kostce 2-wymiarowej, 3 w kostce 3-wymiarowej... W tesserakcie są 4 krawędzie w każdym wierzchołku (też się zgadza). A ile kostek 3-wymiarowych powinniśmy znaleźć w kostce 4-wymiarowej? Kostka jednowymiarowa ma na końcach dwie kostki zerowymiarowe, brzeg kwadratu składa się z czterech kostek jednowymiarowych (odcinków), sześcian ma sześć kwadratowych ścian (2-wymiarowe kostki) - 2, 4, 6, ... Czyżby w czterowymiarowej kostce miało być 8 sześcianów? Fakt, że tam są, spróbujemy pokazać w dalszej części.
Widok z różnych stron
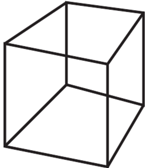
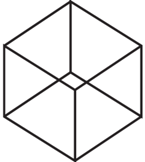
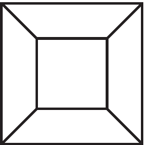
Spójrzmy na trójwymiarowe kostki znajdujące się poniżej, o których, oczywiście, wiemy, że ich ściany są kwadratowe.
Czy nie traktujemy tych rysunków zbyt pobłażliwie? Przecież wcale nie widzimy sześciu, rzekomo kwadratowych ścian! Mimo najszczerszych chęci nie ma możliwości przedstawienia kostki trójwymiarowej w dwóch wymiarach bez zniekształceń. Z wymagania, żeby krawędzie ścian miały takie same długości, ograniczyliśmy się jedynie do tego, żeby każda ze ścian miała tych krawędzi 4. Kątów prostych również się już nie spodziewamy. Nic więc dziwnego, że przedstawienie czterowymiarowej kostki w dwóch wymiarach też nastręcza problemów!
Skoro na rysunku sześcianu wcale nie było sześciu "prostych" kwadratów, to w tesserakcie poszukajmy 8 "krzywych" sześcianów. Tak samo jak kostkę trójwymiarową można przedstawić z różnej perspektywy, tak samo 4-wymiarową. Być może w którejś z nich 8 sześcianów będzie łatwiejszych do zauważenia.
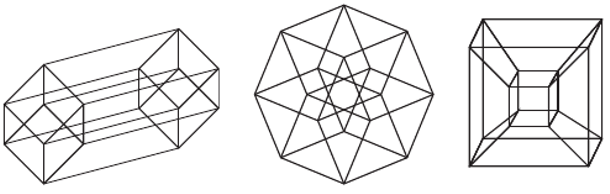
Na rysunku z prawej strony: duży sześcian jest na zewnątrz, mały w środku, a brakujących sześć jest dookoła niego.
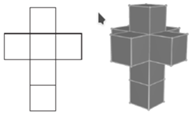
Siatka
Mimo że kostki trójwymiarowej nie przedstawimy wiernie w dwóch wymiarach, to możemy bez żadnych zniekształceń przedstawić jej siatkę! Obok jedna z jedenastu możliwych siatek sześcianu. Podobnie siatkę 4-wymiarowej kostki można przedstawić, bez żadnych zniekształceń, w trzech wymiarach. Oto ona (jedna z wielu siatek tesseraktu)! Sklejać należy już nie krawędzie (kostki 1-wymiarowe), a kwadraty (kostki 2-wymiarowe). Oto film przedstawiający takie sklejanie.
Czterowymiarowe kółko i krzyżyk
A teraz zajmiemy się grą, którą wszyscy dobrze znają: kółko i krzyżyk. O standardowej (czyli płaskiej) grze wszystko wiadomo: dzielimy kwadrat na 9 jednakowych kwadracików i w nie na przemian wstawiamy kółka i krzyżyki. Ten, kto ustawi trzy w jednej linii, wygrywa. W trzech wymiarach postępujemy podobnie: dzielimy sześcian na 27 jednakowych sześcianików i w nich umieszczamy na przemian kółka i krzyżyki a cel gry jest ten sam.
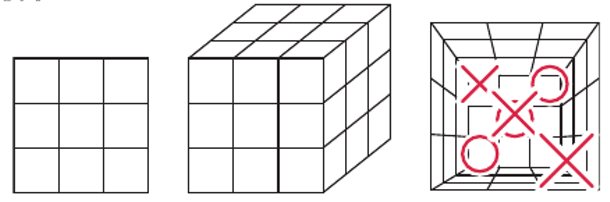
Obrazek z prawej strony przedstawia trójwymiarową rozgrywkę.
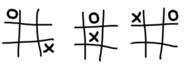
Widok z dołu
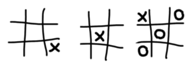
Widok z przodu
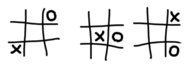
Widok z prawej
Zauważmy, że rozmieszczenie kółek i krzyżyków w sześcianikach możemy zanotować, rysując sytuację na każdym poziomie (rysunki obok).
Czytelnik Spostrzegawczy zauważy, że z jednego z tych rysunków da się odtworzyć pozostałe. A Czytelnik Marudny, że w naszym przykładzie obaj gracze wygrali, co jest przecież niemożliwe. Ale z tego wynika, jak grać w czterech wymiarach. "Po prostu" dzielimy tesserakt na 81 jednakowych tesserakcików, gdzie na każdym poziomie sytuacja jest trójwymiarowa. Przed chwilą ustaliliśmy, jak to zanotować za pomocą trzech sytuacji dwuwymiarowych. A poziomów są trzy. Możemy więc do gry kółko i krzyżyk użyć 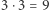 plansz dwuwymiarowych. Wszystko jasne?
plansz dwuwymiarowych. Wszystko jasne?
Wobec tego zadanie: na planszy poniżej kółka mogą wygrać w kolejnym ruchu. Spróbuj znaleźć ten wygrywający ruch (jest więcej niż jeden).

Gdyby jednak wątpliwe było, jak taką planszę rozumieć: każdy wiersz i każda kolumna to trójwymiarowa gra - jest ich 6. Dodatkowo plansze ustawione po skosie to również gry trójwymiarowe. W takim razie mamy 8 trójwymiarowych plansz. W każdym ruchu należy wziąć pod uwagę, czy powstała jakaś wygrywająca linia na którejś z tych 8 plansz trójwymiarowych.
Po paru rozgrywkach Czytelnik pewnie sam się zorientuje, że tak przedstawiona czterowymiarowa gra nie ma większego sensu - to znaczy zakładając racjonalność graczy, pierwszy zawsze wygra. Można jednak nieco zmodyfikować planszę, żeby wyrównać szanse graczy. Wystarczy zamiast planszy 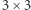 rozważyć
rozważyć 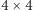 i wziąć 16 takich plansz (4 wiersze z 4 planszami). Udanej gry!
i wziąć 16 takich plansz (4 wiersze z 4 planszami). Udanej gry!