Kilka słów o wymiarze

Ideą teorii wymiaru jest przyporządkowanie przestrzeni
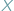 liczby
całkowitej (wymiaru
liczby
całkowitej (wymiaru
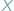 ) tak, by było to zgodne z intuicyjnym znaczeniem
tego słowa. Dla uproszczenia skoncentrujemy się na podzbiorach przestrzeni
Hilberta, która zawiera, między innymi, przestrzenie euklidesowe wszystkich
wymiarów.
) tak, by było to zgodne z intuicyjnym znaczeniem
tego słowa. Dla uproszczenia skoncentrujemy się na podzbiorach przestrzeni
Hilberta, która zawiera, między innymi, przestrzenie euklidesowe wszystkich
wymiarów.
Oczywiste jest, że zbiór złożony ze skończenie wielu punktów ma
wymiar 0, prosta euklidesowa
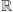 i odcinek – wymiar 1, płaszczyzna
i odcinek – wymiar 1, płaszczyzna
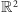 i koło – wymiar 2, a przestrzeń trójwymiarowa
i koło – wymiar 2, a przestrzeń trójwymiarowa
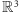 i pełna
kula – wymiar 3. Mając do czynienia z bardzo prostymi obiektami, uznajemy,
że wymiar jest równy odpowiednio 1, 2 lub 3 wtedy, gdy uda się w nim
umieścić odcinek, dwa lub trzy odcinki wzajemnie prostopadłe. Zastanówmy
się, jakie własności powinno mieć przyporządkowanie zbiorowi jego wymiaru.
Wydaje się przede wszystkim, że wymiar powinien być niezmiennikiem
topologicznym. Jeżeli pełny kwadrat ma wymiar 2, to wymiar 2 powinien
mieć także ten sam kwadrat po tym, jak się go powygina i porozciąga
w różnych kierunkach. Spodziewamy się także, że wymiar przestrzeni
i pełna
kula – wymiar 3. Mając do czynienia z bardzo prostymi obiektami, uznajemy,
że wymiar jest równy odpowiednio 1, 2 lub 3 wtedy, gdy uda się w nim
umieścić odcinek, dwa lub trzy odcinki wzajemnie prostopadłe. Zastanówmy
się, jakie własności powinno mieć przyporządkowanie zbiorowi jego wymiaru.
Wydaje się przede wszystkim, że wymiar powinien być niezmiennikiem
topologicznym. Jeżeli pełny kwadrat ma wymiar 2, to wymiar 2 powinien
mieć także ten sam kwadrat po tym, jak się go powygina i porozciąga
w różnych kierunkach. Spodziewamy się także, że wymiar przestrzeni
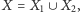 będącej sumą swoich domkniętych podzbiorów
będącej sumą swoich domkniętych podzbiorów
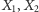 o wymiarach nie większych niż ustalona liczba
o wymiarach nie większych niż ustalona liczba
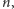 także
nie może być większy od
także
nie może być większy od
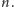 Wynika stąd, że wymiar zbioru
nie może być mniejszy niż wymiary jego podzbiorów. Nie może więc
budzić także żadnych wątpliwości fakt, że wymiar wielościanu musi być
równy największemu spośród wymiarów wszystkich sympleksów
(odcinków, trójkątów, czworościanów itd.), których jest sumą (jest sumą
skończenie wielu).
Wynika stąd, że wymiar zbioru
nie może być mniejszy niż wymiary jego podzbiorów. Nie może więc
budzić także żadnych wątpliwości fakt, że wymiar wielościanu musi być
równy największemu spośród wymiarów wszystkich sympleksów
(odcinków, trójkątów, czworościanów itd.), których jest sumą (jest sumą
skończenie wielu).
W wielu sytuacjach pojawiają się jednak obiekty bardziej złożone. Figury mogą np. być tak skomplikowane, że nie będą zawierać nie tylko żadnego odcinka, ale nawet podzbioru homeomorficznego z odcinkiem, a powinniśmy wiedzieć, w jaki sposób stwierdzić, czy są jedno-, dwu-, trój- czy więcej wymiarowe.
W 1912 roku Henri Poincaré zaproponował, by definicja wymiaru miała charakter indukcyjny oraz odwoływała się do własności rozcinania figury. Punktem wyjścia jego rozważań była obserwacja, że do rozcięcia prostej figury trójwymiarowej na części potrzeba powierzchni, do rozcięcia figury wymiaru 2 potrzebne są linie, a na to, by podzielić na części linię, potrzeba punktów.
Precyzyjną indukcyjną definicję wymiaru sformułowali niezależnie Paweł Uryson
(1922) i Karl Menger (1923). Przyjęli oni, że zbiór pusty jest jedynym zbiorem
o wymiarze równym
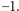 Jeżeli
Jeżeli
 jest liczbą naturalną lub
jest liczbą naturalną lub
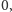 to wymiar
to wymiar
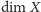 jest nie większy niż
jest nie większy niż
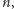 gdy dla
każdego punktu
gdy dla
każdego punktu
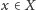 oraz każdego jego otoczenia
oraz każdego jego otoczenia
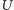 w
w
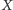 istnieje otwarte otoczenie
istnieje otwarte otoczenie
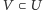 tego punktu, którego
ograniczenie
tego punktu, którego
ograniczenie
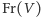 ma wymiar
ma wymiar
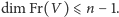 Jeżeli
Jeżeli
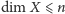 i nie jest prawdą, że
i nie jest prawdą, że
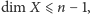 to przyjmujemy,
że
to przyjmujemy,
że
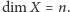 Jeżeli
Jeżeli
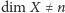 dla
dla
 to
mówimy, że wymiar
to
mówimy, że wymiar
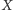 jest nieskończony i piszemy
jest nieskończony i piszemy
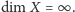
Konsekwencją tej definicji jest np. to, że przestrzeń euklidesowa
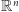 i kostka wymiaru
i kostka wymiaru
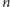 nie mogą być rozcinane przez
zbiory o wymiarze mniejszym niż
nie mogą być rozcinane przez
zbiory o wymiarze mniejszym niż
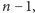 natomiast podzbiór
natomiast podzbiór
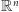 może sam mieć wymiar
może sam mieć wymiar
 tylko wtedy, gdy ma punkty
wewnętrzne, czyli zawiera kulę otwartą przestrzeni euklidesowej.
tylko wtedy, gdy ma punkty
wewnętrzne, czyli zawiera kulę otwartą przestrzeni euklidesowej.
Mówimy, że zbiór
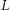 jest przegródką między rozłącznymi
podzbiorami
jest przegródką między rozłącznymi
podzbiorami
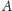 i
i
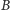 zbioru
zbioru
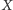 albo przegródką oddzielającą
albo przegródką oddzielającą
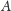 od
od
 jeżeli
jeżeli
 gdzie
gdzie
 i
i
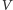 są takimi rozłącznymi otwartymi podzbiorami
są takimi rozłącznymi otwartymi podzbiorami
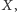 że
że
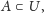
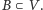 Oznacza to w szczególności, iż
Oznacza to w szczególności, iż
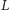 jest
domkniętym podzbiorem
jest
domkniętym podzbiorem
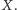 Odcinek łączący środki dwóch
przeciwległych boków kwadratu jest przegródką oddzielającą dwa pozostałe
boki. Żaden podzbiór kwadratu, położony w jego wnętrzu, nie może,
oczywiście, ich oddzielać.
Odcinek łączący środki dwóch
przeciwległych boków kwadratu jest przegródką oddzielającą dwa pozostałe
boki. Żaden podzbiór kwadratu, położony w jego wnętrzu, nie może,
oczywiście, ich oddzielać.
Wymiar przestrzeni można scharakteryzować, używając pojęcia przegródek.
Nierówność
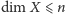 zachodzi mianowicie wtedy i tylko wtedy, gdy dla
dowolnych rozłącznych podzbiorów domkniętych
zachodzi mianowicie wtedy i tylko wtedy, gdy dla
dowolnych rozłącznych podzbiorów domkniętych
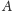 i
i
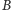 istnieje
przegródka
istnieje
przegródka
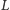 oddzielająca
oddzielająca
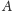 od
od
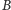 o wymiarze
o wymiarze
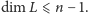
Na płaszczyźnie euklidesowej jest znacznie więcej miejsca niż na prostej i mniej
niż w przestrzeni trójwymiarowej. Uogólniając to, możemy się spodziewać,
że w przestrzeni o większym wymiarze musi być więcej miejsca niż
w przestrzeni o wymiarze mniejszym. Jeżeli
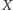 jest przestrzenią zwartą,
to okazuje się, na przykład, że nierówność
jest przestrzenią zwartą,
to okazuje się, na przykład, że nierówność
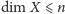 zachodzi
wtedy i tylko wtedy, gdy dla każdego pokrycia
zachodzi
wtedy i tylko wtedy, gdy dla każdego pokrycia
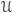 przestrzeni
przestrzeni
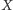 zbiorami otwartymi można znaleźć drobniejsze pokrycie
otwarte
zbiorami otwartymi można znaleźć drobniejsze pokrycie
otwarte
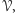 które daje się rozłożyć na sumę
które daje się rozłożyć na sumę
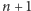 rodzin
rodzin
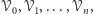 takich że zbiory należące do jednej ustalonej rodziny
takich że zbiory należące do jednej ustalonej rodziny
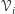 są parami rozłączne (
są parami rozłączne (
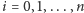 ). Można także wykazać,
iż nierówność
). Można także wykazać,
iż nierówność
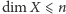 jest równoważna temu, że dla
każdego skończonego pokrycia otwartego przestrzeni
jest równoważna temu, że dla
każdego skończonego pokrycia otwartego przestrzeni
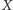 można
znaleźć takie drobniejsze pokrycie skończone, że przecięcie każdych
można
znaleźć takie drobniejsze pokrycie skończone, że przecięcie każdych
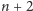 różnych zbiorów otwartych należących do niego jest
zbiorem pustym.
różnych zbiorów otwartych należących do niego jest
zbiorem pustym.
Można się zastanawiać, czy lepszym i bliższym intuicji podejściem do
problemu sformułowania ogólnej definicji wymiaru nie byłaby redukcja
naszego zadania do badania wymiarów wielościanów coraz lepiej
aproksymujących przestrzeń, której wymiar chcemy określić. Okazuje
się jednak, że idąc tą drogą, otrzymuje się dokładnie to samo pojęcie,
co poprzednio. Zbiór zwarty
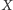 ma w szczególności wymiar
nie większy niż
ma w szczególności wymiar
nie większy niż
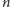 wtedy i tylko wtedy, gdy dla każdego
wtedy i tylko wtedy, gdy dla każdego
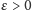 istnieje przekształcenie
istnieje przekształcenie
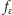 w przestrzeń o tej własności,
że punkt
w przestrzeń o tej własności,
że punkt
 oraz jego obraz
oraz jego obraz
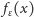 są oddalone o mniej niż
są oddalone o mniej niż
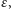 natomiast obraz całego
natomiast obraz całego
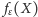 jest wielościanem wymiaru
co najwyżej
jest wielościanem wymiaru
co najwyżej