Hipoteza Poincarégo
_thumb_190px.jpg)
Wikipedia
Grigorij Jakowlewicz Perelman
11 listopada 2002 roku Grigorij Jakowlewicz Perelman, geometra pracujący
w Petersburskim Oddziale Instytutu Matematycznego im. Stiekłowa przy
Fontance 27, udostępnił w Internecie 40-stronicową pracę pod tytułem
„Formuła entropii dla potoku Ricciego i jej zastosowania geometryczne”.
Czwartą stronę suchego i najeżonego fachowymi terminami wprowadzenia
kończy zdanie:
Wreszcie, w rozdziale 13, podajemy krótki szkic dowodu
hipotezy geometryzacyjnej.
Wspomniana hipoteza pochodzi od Williama Thurstona i dotyczy budowy trójwymiarowych rozmaitości. Jest tak ogólna i potężna, że słynna hipoteza Poincarégo – jeden z siedmiu problemów za milion dolarów z listy Instytutu Claya, patrz Aktualności, Delta 8/2000 – wypływa z niej jako prosty wniosek.
10 marca 2003 roku Perelman udostępnił drugą pracę, Potok Ricciego z chirurgią na rozmaitościach trójwymiarowych. Szkic dowodu z pierwszego preprintu został w niej opisany znacznie dokładniej.
W kwietniu 2003 roku Perelman wygłaszał serie wykładów na kilku znanych uniwersytetach amerykańskich, a w kilku miejscach świata ekipy ekspertów zaczęły podczas wielotygodniowych seminariów brnąć przez jego prace, napisane z bolesną zwięzłością. Pojawiły się niezależne dowody niektórych twierdzeń z obu prac Perelmana, a on sam napisał w lipcu 2003 trzeci preprint, podając uproszczoną wersję swego dowodu tego przypadku hipotezy geometryzacyjnej Thurstona, który wystarcza do wnioskowania o prawdziwości hipotezy Poincarégo. W chwili, gdy piszę te słowa, ostatecznej i zgodnej opinii fachowców jeszcze nie ma, ale wiele osób wyraża nie bez powodu ostrożny optymizm. Cała sprawa wygląda na tyle poważnie, że wypada o niej opowiedzieć Czytelnikom Delty.
1.
Od ponad stu lat znamy listę wszystkich zwartych, orientowalnych rozmaitości
dwuwymiarowych, tzn. takich powierzchni, które mają dwie strony, a za to nie
mają ani brzegu, ani żadnych nakłuć czy rozcięć, ani powyciąganych
nieskończenie daleko odnóg. Jest to lista ponumerowana wszystkimi liczbami
naturalnymi; na jej pierwszym miejscu figuruje sfera
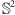 , na drugim
– torus
, na drugim
– torus
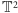 , na trzecim – precel, który uzyskujemy wyciąwszy
w torusie dwa otwory i dokleiwszy w to miejsce rurkę itd. Otrzymujemy
w ten sposób, jak mówi matematyk, klasyfikację z dokładnością
do homeomorfizmu: dwie powierzchnie uznajemy za identyczne, jeśli istnieje
ciągłe i różnowartościowe przekształcenie jednej z nich na drugą. Oznacza
to, że powierzchnię symetrycznego torusa obrotowego utożsamiamy
z powierzchnią kubka z jednym uchem. (Więcej na temat dwuwymiarowych
powierzchni – patrz artykuł J. Górnickiego Kilka słów o powierzchniach,
Delta 6/1995.)
, na trzecim – precel, który uzyskujemy wyciąwszy
w torusie dwa otwory i dokleiwszy w to miejsce rurkę itd. Otrzymujemy
w ten sposób, jak mówi matematyk, klasyfikację z dokładnością
do homeomorfizmu: dwie powierzchnie uznajemy za identyczne, jeśli istnieje
ciągłe i różnowartościowe przekształcenie jednej z nich na drugą. Oznacza
to, że powierzchnię symetrycznego torusa obrotowego utożsamiamy
z powierzchnią kubka z jednym uchem. (Więcej na temat dwuwymiarowych
powierzchni – patrz artykuł J. Górnickiego Kilka słów o powierzchniach,
Delta 6/1995.)

Rys. 1 Sfera, torus i precel. Kolorowych krzywych na torusie i preclu nie można w sposób ciągły zdeformować do punktu.
Zwróćmy uwagę, że wśród tych powierzchni jedynie sfera ma tę własność, że każdą położoną na niej krzywą zamkniętą można w sposób ciągły, bez rozrywania, zdeformować do punktu. Na torusie i na wszelkich preclach jest masa krzywych, których do punktu bez rozrywania zdeformować się nie da.
2.
Rozmaitości trójwymiarowe to możliwe formy naszej przestrzeni. Więcej informacji na ten temat można znaleźć w artykule Zbigniewa Marciniaka opublikowanym pod takim właśnie tytułem w Delcie 5/1997.
Przykłady zwartych rozmaitości trójwymiarowych to
- (a)
- sfera
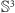 , czyli
zbiór tych punktów
, czyli
zbiór tych punktów
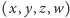 przestrzeni czterowymiarowej,
których współrzędne spełniają warunek
przestrzeni czterowymiarowej,
których współrzędne spełniają warunek
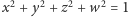 ,
,
- (b)
- torus
 , czyli rozmaitość, którą uzyskuje się, sklejając pary
przeciwległych ścian sześcianu,
, czyli rozmaitość, którą uzyskuje się, sklejając pary
przeciwległych ścian sześcianu,
- (c)
- produkt kartezjański okręgu i precla z rysunku 1.
Osobom, które stwierdzą, że nie ma po co myśleć o jakichś tam rozmaitościach, bo przecież przestrzeń wokół nas jest euklidesowa i każdy to widzi, pragnę przypomnieć, że przez setki lat prawie wszyscy „widzieli”, że Ziemia jest płaska.
3.
W 1904 roku Poincaré wyraził przypuszczenie, że sferę
 spośród
innych trójwymiarowych rozmaitości zwartych wyróżnia ta sama
własność, która charakteryzuje o jeden wymiar niżej jej koleżankę
spośród
innych trójwymiarowych rozmaitości zwartych wyróżnia ta sama
własność, która charakteryzuje o jeden wymiar niżej jej koleżankę
 . Mianowicie,
. Mianowicie,
jeśli na trójwymiarowej zwartej rozmaitości
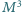 (bez brzegu) każdą
krzywą zamkniętą można w sposób ciągły zdeformować do punktu, to
(bez brzegu) każdą
krzywą zamkniętą można w sposób ciągły zdeformować do punktu, to
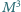 jest homeomorficzna ze sferą
jest homeomorficzna ze sferą
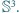
To właśnie jest hipoteza Poincarégo. Co ciekawe, jej uogólnienia na
rozmaitości wymiaru
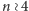 zostały już udowodnione.
zostały już udowodnione.
4.
W końcu lat 70. XX wieku Thurston wysunął dalekosiężną hipotezę, głoszącą,
że każdą rozmaitość trójwymiarową można rozciąć – prowadząc
(dwuwymiarowe) cięcia wzdłuż sfer
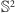 lub torusów
lub torusów
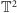 –
na skończoną liczbę części, z których każdą można wyposażyć w jedną
z modelowych geometrii. Oznacza to, mówiąc mętnie, że na każdej części
można tak określić sposób pomiaru odległości, by inteligentne zielone
ludziki wyposażone wyłącznie w taśmę mierniczą nie potrafiły w obrębie
danej części odróżniać rozmaitych miejsc przestrzeni, gdyż wszystko
wszędzie wygląda identycznie i jeśli nawet pojawiają się jakieś zakrzywienia
czy skręcenia przestrzeni, to ich struktura jest w każdym punkcie taka sama.
W wymiarze 2 dobre przykłady takiej sytuacji to zwykła płaszczyzna,
sfera
–
na skończoną liczbę części, z których każdą można wyposażyć w jedną
z modelowych geometrii. Oznacza to, mówiąc mętnie, że na każdej części
można tak określić sposób pomiaru odległości, by inteligentne zielone
ludziki wyposażone wyłącznie w taśmę mierniczą nie potrafiły w obrębie
danej części odróżniać rozmaitych miejsc przestrzeni, gdyż wszystko
wszędzie wygląda identycznie i jeśli nawet pojawiają się jakieś zakrzywienia
czy skręcenia przestrzeni, to ich struktura jest w każdym punkcie taka sama.
W wymiarze 2 dobre przykłady takiej sytuacji to zwykła płaszczyzna,
sfera
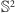 i płaszczyzna Łobaczewskiego. Thurston wykazał, że
w wymiarze 3 takich eleganckich modelowych geometrii jest dokładnie
osiem.
i płaszczyzna Łobaczewskiego. Thurston wykazał, że
w wymiarze 3 takich eleganckich modelowych geometrii jest dokładnie
osiem.
5.
Mniej więcej 20 lat temu Hamilton nakreślił śmiały program prac nad hipotezą geometryzacyjną Thurstona. Oto zarys pomysłu: należy wziąć rozmaitość, wyposażyć w jakąkolwiek metrykę, a następnie puścić w ruch, w taki sposób, aby prędkości różnych punktów zależały (w jakiś sposób) od krzywizny w danym miejscu. Po co? Otóż po to, żeby najlepiej cała rozmaitość, albo przynajmniej jej pokaźne fragmenty, nabrały zgrabnego, symetrycznego kształtu.
O prostym przykładzie podobnego ruchu krzywych i powierzchni – tzw. ewolucji krzywiznowej i średniokrzywiznowej – można poczytać w Delcie 4/2003. Odsyłam tam po nieco więcej szczegółów; wspomnę tu jedynie, że jeśli prędkość zamkniętej krzywej płaskiej jest równa krzywiźnie i skierowana wzdłuż wektora normalnego, to wszelkie fałdki, wklęsłości i zawijasy owej krzywej ulegają stopniowemu wygładzeniu i koniec końców krzywa przypomina idealny okrąg. Zupełnie nie ma znaczenia, jak wyglądała na początku. W przypadku powierzchni jest gorzej – mogą pojawiać się rozmaite osobliwości, gdyż cieniutkie rureczki kurczą się znacznie szybciej niż pękate bąble.

Rys. 2 Wąska rurka kurczy się szybciej niż pozostałe części rozmaitości. Aby zapobiec katastrofie, należy dokonać zapobiegawczej chirurgii: zawczasu wyciąć kolorową część rurki, a dwa otwory zalepić małymi czapeczkami. Rozdzielone części ewoluują dalej osobno.
W wymiarze 3 należy, po pierwsze – odpowiednio zdefiniować sam „ruch” rozmaitości, po drugie – wykazać istnienie rozwiązań, po trzecie – przewidzieć charakter osobliwości i jak najdokładniej je opisać, po czwarte – nauczyć się zapobiegać występowaniu osobliwości poprzez sprytne rozcinanie rozmaitości na odpowiednie części w odpowiednich miejscach (patrz rys. 2). Po piąte – trzeba to robić tak, żeby zachować kontrolę nad kształtem i topologią odcinanych fragmentów.
Łatwo powiedzieć, trudniej zrobić. Hamilton zaproponował, żeby
deformować metrykę z prędkością równą minus podwojonej krzywiznie
Ricciego, tzn. na danej rozmaitości
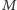 budować taką rodzinę
zależnych od czasu
budować taką rodzinę
zależnych od czasu
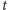 metryk riemannowskich
metryk riemannowskich
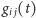 , by
, by
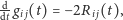
gdzie
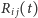 jest tensorem Ricciego określonym przez metrykę w chwili
jest tensorem Ricciego określonym przez metrykę w chwili
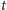 . Rodzina
. Rodzina
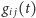 to właśnie potok Ricciego.
to właśnie potok Ricciego.
Czytelnik, który nie wie, co to jest metryka riemannowska i krzywizna Ricciego, nie powinien się przejmować, tylko przywołać przed oczy wyimaginowany obraz powyginanej przestrzennej siateczki do pomiaru odległości, pól i objętości, czegoś w rodzaju trójwymiarowego i powykrzywianego odpowiednika papieru milimetrowego (a jeszcze lepiej przezroczystej folii milimetrowej). Należy sobie wyobrazić, że owa siateczka ożywa i zaczyna się poruszać, płynnie zmieniając kształty. Prędkości są w różnych miejscach różne. Co się dzieje z odległościami? Aby odpowiedzieć na to pytanie, należy ustalić w przestrzeni punkt i kierunek, a następnie przeanalizować krzywiznę wszystkich niewielkich dwuwymiarowych „płatków” przestrzeni, które są w tym punkcie styczne do owego kierunku (w zwykłej przestrzeni euklidesowej byłby to pęk płaszczyzn). Jeśli wśród owych płatków przeważają takie, które wyglądają jak fragmenty powierzchni sfery czy elipsoidy, to odległość w danym kierunku się zmniejsza, gdy czas rośnie. Jeśli więcej jest płatków w kształcie siodeł, to odległość w danym kierunku rośnie wraz z upływem czasu.
Lokalnie, w tak zwanych normalnych układach współrzędnych, wygląda to niemal tak, jakby wszystkie współrzędne metryki spełniały, przy odpowiednim wyborze jednostek czasu, zwykłe równanie przewodnictwa cieplnego (patrz Delta 12/1998). Niemal, gdyż obecne jest nieliniowe zaburzenie, co sprawia, że z owego lokalnego obrazka nie można pochopnie wyciągać globalnych i dalekosiężnych wniosków. Wiadomo jednak, że równanie przewodnictwa cieplnego wygładza wszelkie początkowe nieregularności temperatury (jak się włoży dużą i mocną grzałkę do wiadra, to w końcu cała woda się zagotuje). Stąd nadzieja, że potok Ricciego pomaga nadawać wszelkim rozmaitościom porządną, regularną strukturę geometryczną.
Hamilton wykazał istnienie rozwiązań potoku Ricciego na małych przedziałach czasu. W wielu pracach powstałych w latach 1982–1997 opisał liczne własności tego potoku i jego zachowanie w rozmaitych szczególnych przypadkach. Nie udało mu się jednak opracować odpowiedniego systemu kontroli osobliwości ani wykluczyć pojawiania się osobliwości szczególnie niepożądanych, które w żargonie nazywa się cygarami, z tego względu, że fragment rozmaitości zaczyna wtedy wyglądać mniej więcej tak, jak produkt kartezjański okręgu i powierzchni szalenie długiego i cienkiego czubka cygara. A bez takiego systemu kontroli nie ma co marzyć o zapobiegawczych chirurgiach i o przedłużaniu potoku Ricciego poza osobliwości.
6.
Cóż więc zrobił Perelman? Po pierwsze, korzystając z prac Hamiltona
o łącznej objętości ponad 400 stron, skonstruował narzędzia, dzięki którym
można dostrzegać i w pełni kontrolować nadchodzące osobliwości. Jest to
skrajnie trudne dlatego, że osobliwości mogą narastać w różnym tempie,
w różnych miejscach i w różnych skalach. Po drugie, opracował taką
metodę wyboru chwil, w których dokonuje się zapobiegawczych chirurgii, że
po skończonej liczbie cięć wzdłuż sfer i oddzieleniu od wyjściowej
rozmaitości kawałków o ściśle kontrolowanych kształtach zostaje jeszcze
„coś”, w czym można wyróżnić części „grube” i części „cienkie”,
posklejane wzdłuż torusów
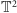 . To „coś” może być wprawdzie
bardzo zawiłe, ale jego strukturę eksperci od geometrii trójwymiarowych
rozmaitości rozumieją na tyle dobrze, żeby dokładnie opisać wygląd części
grubych i cienkich dla dużych czasów
. To „coś” może być wprawdzie
bardzo zawiłe, ale jego strukturę eksperci od geometrii trójwymiarowych
rozmaitości rozumieją na tyle dobrze, żeby dokładnie opisać wygląd części
grubych i cienkich dla dużych czasów
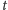 . I to (podobno) już
wystarczy...
. I to (podobno) już
wystarczy...
Prace Perelmana są niezwykle bogate. Prócz ogromu wyobraźni geometrycznej są w nich oczywiście równania różniczkowe opisujące, jak z upływem czasu zmienia się metryka, krzywizna, objętości kul itp., jest masa nierówności całkowych, są analogie i intuicje czerpane z fizyki statystycznej, jest wreszcie pomysłowy funkcjonał entropii, który pozwala wykluczyć pojawianie się niepożądanych cygar. Wszyscy są zgodni, że nawet jeśli gdzieś znajdzie się jeszcze jakaś luka, która spowoduje, że hipoteza Thurstona i hipoteza Poincarégo pozostaną hipotezami, to i tak to, co już zostało sprawdzone, jest wielkim osiągnięciem.
7.
Uprawianie matematyki często porównuje się do chodzenia po wysokich górach. Nie jest to całkowicie pozbawione sensu, gdyż jedną z możliwych odpowiedzi na pytanie, dlaczego właściwie zajmować się hipotezą Poincarégo, jest odpowiedź moralnego zdobywcy Everestu, Mallory’ego: w góry chodzi się dlatego, że są.
Nie wiem, czy Perelman chodzi po górach. Przypomniała mi się jednak z tej okazji Piosenka o górach Włodzimierza Wysockiego, w której narrator, wszak również alpinista, miesza pokorę wobec majestatu gór i śniegów tających imiona poległych z nutką zawadiackiej dumy z przebytej właśnie nowej drogi. Nieudolnie kartkując wspomniane wyżej preprinty i liczne do nich uzupełnienia i komentarze, wielekroć myślałem, że Grisza Perelman miałby pełne prawo tę piosenkę nucić.