- Spokojnie Basiu, powiedz mi dokładnie, o czym mówisz - poprosił tata, choć już się domyślał, o czym będzie rozmowa. Kilka miesięcy temu, siostry kłóciły się o to, kto powinien tego dnia wynieść śmieci. Żeby rozstrzygnąć spór, tata zaproponował, że osoba wykonująca obowiązek będzie wybierana poprzez rzut monetą. Tym systemem udało się pogodzić siostry; jak widać, nie na długo. Basia wzięła wdech i zaczęła mówić:

- Niedawno zauważyłam, że jak Kasia rzuca monetą, to o wiele częściej wypada reszka, więc stwierdziłam, że chyba nauczyła się tak rzucać, by częściej tak wypadało. Dlatego zaczęłam liczyć i w ciągu ostatnich dwóch tygodni orzeł wypadł 5 razy, a reszka 9! To jest prawie dwa razy częściej! Kasia oszukuje!

Tata się uśmiechnął i zapytał:

- A wiesz, jakie jest prawdopodobieństwo, że w 14 rzutach orzeł wypadnie 5 razy?

- Nie wiem.

- Jak rzucamy monetą 14 razy, to możemy otrzymać 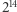możliwości. A wyrzucić 5 orłów i 9 reszek możemy na 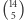sposobów. A 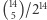to około 12%.

- To bardzo mało!

- To mało, jednak chyba nie na tyle, żeby zarzucać siostrze nieuczciwość. Zwłaszcza że tak naprawdę powinniśmy odpowiedzieć sobie na pytanie, jaka jest szansa na to, że otrzymamy co najwyżej 5 reszek, gdyż każdy z takich wyników wzbudziłby Twoje wątpliwości. Można policzyć, że to prawdopodobieństwo jest równe około 21%. To więcej, niż szansa na wyrzucenie 6 oczek przy jednokrotnym rzucie kostką, a chyba nie podejrzewałabyś Kasi o oszukiwanie w takiej sytuacji?

W tym momencie Basia zrobiła smutną minę. Owszem, podejrzewałaby swoją siostrę nawet w takiej sytuacji, ale wiedziała już, że nic nie wskóra. Chcąc poprawić jej humor, tata zaproponował:

- Może chcesz sprawdzić statystycznie, czy masz rację? Mogę Ci pokazać, jak to zrobić. Statystyki można używać, żeby udowadniać innym swoje racje. Jednak, co jest równie ważne, statystyka pomaga nam się także dowiedzieć, czy sami mamy rację. To jak, chcesz spróbować?

Dziewczynka kiwnęła głową.

- W statystyce mówimy o hipotezie zerowej, może o niej słyszałaś. Otóż, gdy wykonujemy test statystyczny, mamy dwie hipotezy. Pierwsza z nich jest czymś, w co wierzy większość ludzi, czymś uznawanym przez większość osób za prawdę lub czymś, do czego po prostu jesteśmy przyzwyczajeni i nie chcielibyśmy się z tym przeświadczeniem rozstawać, nie mając ku temu solidnych podstaw. Druga jest naszym przypuszczeniem. To, co ważne, to pytanie, jakie sobie zadajemy. Wiesz jakie, Basiu?

- Która z hipotez jest bardziej prawdopodobna?

- Właśnie nie. Wytłumaczę Ci to na przykładzie. Niektórzy ludzie wierzą, że jeśli wyjdą z domu bez parasola, to jest większe prawdopodobieństwo, że spadnie deszcz, że los robi im na złość. Wyobraź sobie, że jest taki człowiek i liczy dni, patrząc, czy wziął parasol i czy spadł deszcz.

Otrzymujemy takie dane:

Te dane wyglądają sugestywnie, aż chce się stwierdzić, że świat faktycznie robi nam na złość. Wydaje się, że według danych jest to bardziej prawdopodobne, ale mimo wszystko prawdopodobieństwo, że deszcz i parasol nie mają związku, a taki wynik otrzymaliśmy przypadkiem, może być duże. Żeby je wyliczyć, możemy użyć pewnej procedury statystycznej, zwanej testem Chi-Kwadrat. Jesteś jeszcze za młoda, by poznać szczegóły, wystarczy jednak wiedzieć, że procedura ta pozwala w przybliżony sposób obliczać prawdopodobieństwa określonych odstępstw od oczekiwanych wyników. Gdy ją zastosujemy, to okaże się, że jeżeli deszcz i parasol są niezależne, to prawdopodobieństwo tak "sugestywnych" wyników, jakie uzyskaliśmy, jest równe około 36%. Nie jest to mało, zatem wnioskowanie, że deszcz i parasol wpływają na siebie, wypada uznać za bezpodstawne. Dlatego w przypadku takich problemów należy zadawać następujące pytanie:

Jeżeli istnieje ogólnie przyjęta hipoteza "bazowa",
... a ja mam własną hipotezę, która lepiej oddaje rzeczywistość,
... jakie jest prawdopodobieństwo, że mimo wszystko hipoteza bazowa jest poprawna?

Basia spojrzała na tatę z niezrozumieniem, dlatego ten kontynuował:

- W 14 rzutach otrzymałyście 5 orłów. To ci powiedziało, że "Kasia rzuca monetą w podejrzany sposób". Jednak jak się okazuje, jeżeli Kasia jest niewinna, to prawdopodobieństwo, że orły będą wypadać tak rzadko lub rzadziej, jest mniej więcej 21%. To nie tak mało. A to, że orłów jest prawie dwa razy mniej niż reszek, nie ma wielkiego znaczenia, bo rzuciłyście bardzo mało razy.

Tata na chwilę zamilkł, pomyślał i powiedział:

- Proponuję ci, Basiu, byś teraz liczyła, jak często wypadają orzeł i reszka przez trzy miesiące. Jak będziesz miała dużo danych, to zrobimy statystyczny test, który nam powie, czy masz rację, czy nie. Dobrze?

Basia zgodziła się na propozycję taty. Po 90 dniach wróciła z wynikiem:

- Policzyłam. W ciągu ostatnich 90 dni reszka wypadła 54 razy, a orzeł 36 razy.

- A widzisz, teraz reszek nie jest dwa razy więcej niż orłów.

- Ale wciąż jest ich dużo, stosunek reszek do orłów jest jak 3 do 2.

- Takie rzeczy mogą się zdarzyć, to przecież rzut monetą.

- Ale tato, zróbmy ten test!

W tym momencie tata przypomniał sobie o danej obietnicy i się zreflektował:

- Oczywiście, zrobimy tak, naszą hipotezą zerową jest to, że orły i reszki są tak samo częste. Twoją hipotezą, Basiu, jest to, że orły są rzadsze. Faktycznie tak to wygląda z twoich wyliczeń. To teraz zadajmy sobie pytanie: jak bardzo możliwe jest to, że orły są tak samo częste, a wypadło ich nie więcej niż 36 w 90 rzutach?

Tata spojrzał na Basię i dodał:

- Jest jeszcze jedna rzecz, którą powinnaś wiedzieć: statystycy wyliczają to prawdopodobieństwo i nazywają je 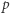-wartością. W naszej sytuacji możemy przyjąć, że 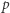-wartość mniejsza od 5% da nam istotne podstawy do odrzucenia hipotezy zerowej o uczciwości Kasi. Rozumiesz mnie, Basiu?

Dziewczynka zaczęła powoli mówić:

- Kasia wyrzuciła dużo reszek. To sprawia, że moja… hipoteza brzmi lepiej, a ja czuję się oszukana. Jednak Kasia może jest uczciwa i będzie jej smutno, kiedy ją oskarżę. Dlatego sprawdzimy, jakie jest prawdopodobieństwo, że Kasia nic nie zrobiła, a mi się tylko wydaje, że kłamie. Jeżeli będzie odpowiednio duże, to stwierdzimy, że to los. Prawda?

Tata się rozpromienił i kiwnął głową. Po chwili zaczął wpisywać odpowiednie wyliczenia w komputer.

- To teraz sprawdzimy, jakie jest prawdopodobieństwo takiego zdarzenia. Otóż jest ono równe... 3,6%.

Zamilkł na chwilę, a Basia spojrzawszy na niego tryumfalnie, zapytała:

- Czyli prawdopodobieństwo, że Kasia jest uczciwa, jest małe, prawda? Czyli pójdziemy z nią porozmawiać, tato?

- Tak Basiu, pójdziemy.