Testy serii
W języku potocznym spotykamy się czasem ze słowem seria, które może oznaczać zbiór jednakowych lub w pewien sposób powiązanych ze sobą przedmiotów, jak np. seria znaczków pocztowych czy seria wyrobów przemysłowych. Serią nazywamy również ciąg następujących po sobie czynności lub zdarzeń - w tym sensie rozumie się tzw. czarną serię wypadków, serię wystrzałów itp. Pojęcie serii okazuje się być przydatne także w matematyce. Zanim przedstawimy ciekawe zastosowania serii do konstrukcji użytecznych testów statystycznych, uściślijmy, co będziemy rozumieć pod pojęciem serii.
Załóżmy, że mamy 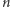 obiektów dwojakiego rodzaju, w tym
obiektów dwojakiego rodzaju, w tym 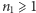 obiektów pierwszego oraz
obiektów pierwszego oraz 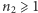 obiektów drugiego rodzaju, przy czym
obiektów drugiego rodzaju, przy czym 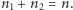 Przyjmijmy ponadto, że jesteśmy w stanie w jakiś sposób uporządkować te obiekty. Odtąd natura owych obiektów nie będzie mieć już dla nas znaczenia. Nie będziemy ich też rozróżniać, pamiętając jedynie to, jakiego są one rodzaju. W ten sposób otrzymujemy pewien ciąg symboli, np.:
Przyjmijmy ponadto, że jesteśmy w stanie w jakiś sposób uporządkować te obiekty. Odtąd natura owych obiektów nie będzie mieć już dla nas znaczenia. Nie będziemy ich też rozróżniać, pamiętając jedynie to, jakiego są one rodzaju. W ten sposób otrzymujemy pewien ciąg symboli, np.:
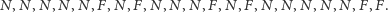 |
Powyższy ciąg odzwierciedla wyniki pojedynków tenisowych między Rogerem Federerem i Rafaelem Nadalem (w turniejach wielkoszlemowych, ATP i Pucharu Davisa) w ciągu ostatnich dziewięciu lat, przy czym symbole 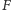 i
i 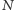 oznaczają, odpowiednio, zwycięstwo Federera i Nadala.
oznaczają, odpowiednio, zwycięstwo Federera i Nadala.

Mając taki ciąg symboli, serią nazywamy podciąg symboli tego samego rodzaju, który poprzedza i po którym występuje symbol innego rodzaju (lub żaden symbol, w przypadku pierwszej i ostatniej serii). Łatwo zauważyć, że w rozważanym powyżej ciągu mamy 10 serii:
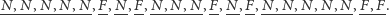 |
Okazuje się, że liczba serii występujących w badanym ciągu obiektów dostarcza informacji, które mogą być przydatne we wnioskowaniu statystycznym, co wykażemy, przedstawiając konstrukcję dwóch testów i ilustrując ich działanie na przykładach.
Rozpoczniemy od testu równości dwóch rozkładów. Załóżmy, że mamy dwie niezależne próbki losowe 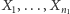 i
i 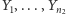 składające się z niezależnych obserwacji. Interesuje nas, czy rozkłady, z których pochodzą te próbki, różnią się istotnie. Zakładając, że wśród obserwacji nie ma powtarzających się wartości, możemy ustawić je w ciąg rosnący. Jeśli teraz pominiemy wartości obserwacji, a pozostawimy tylko etykiety, wskazujące, czy dany pomiar związany był z pierwszą czy z drugą próbką, otrzymamy ciąg
składające się z niezależnych obserwacji. Interesuje nas, czy rozkłady, z których pochodzą te próbki, różnią się istotnie. Zakładając, że wśród obserwacji nie ma powtarzających się wartości, możemy ustawić je w ciąg rosnący. Jeśli teraz pominiemy wartości obserwacji, a pozostawimy tylko etykiety, wskazujące, czy dany pomiar związany był z pierwszą czy z drugą próbką, otrzymamy ciąg 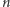 symboli złożony z iksów i igreków, gdzie
symboli złożony z iksów i igreków, gdzie 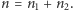 Przykładowo, dla
Przykładowo, dla 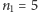 oraz
oraz 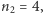 moglibyśmy otrzymać
moglibyśmy otrzymać
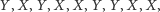 |
(1) |
co oznaczałoby, że najmniejsza obserwacja należy do próbki igreków, druga co do wielkości - do iksów itd., aż po największą obserwację, która także pochodzi z pierwszej próbki. Zauważmy, że to, jak rozłożą się iksy i igreki, może nam sporo powiedzieć na temat rozkładów obu próbek. Faktycznie, gdybyśmy otrzymali
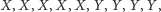 |
(2) |
byłby to sygnał sugerujący, że iksy są zasadniczo mniejsze niż igreki. Z kolei następująca konfiguracja
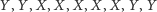 |
(3) |
wskazywałaby, że igreki pochodzą z rozkładu charakteryzującego się większym rozrzutem niż rozkład iksów. Natomiast ciąg postaci
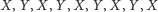 |
świadczyłby o dobrym wymieszaniu obserwacji obu próbek. Ostatni przykład, w przeciwieństwie do dwóch poprzednich, mógłby sugerować, że obie próbki pochodzą z tego samego rozkładu. Zauważmy, że w tym ostatnim ciągu występuje aż 9 serii, podczas gdy w ciągach (2) i (3) mieliśmy, odpowiednio, tylko 2 i 3 serie. Biorąc pod uwagę wspomniane wyżej interpretacje poszczególnych ciągów, możemy wysnuć przypuszczenie, że gdy w ciągu otrzymanym z połączenia obu próbek jest mało serii, to wskazuje to raczej na istotne różnice między rozkładami obu próbek, podczas gdy duża liczba serii może sugerować, że obie próbki pochodzą de facto z tego samego rozkładu. Tego typu spostrzeżenia nasunęły Abrahamowi Waldowi i Jakubowi Wolfowitzowi pomysł konstrukcji następującego testu statystycznego: jeśli liczba serii występujących w ciągu otrzymanym z połączonych próbek jest mała, to odrzucamy hipotezę mówiącą o braku różnic między rozkładami, natomiast w przeciwnym przypadku, tzn. gdy liczba serii jest duża, nie mamy podstaw do odrzucenia rozważanej hipotezy, co w praktyce oznacza stwierdzenie braku istotnej różnicy między rozkładami.
W tym miejscu konieczne jest poczynienie pewnych uwag. Po pierwsze, musimy być świadomi, że nawet gdyby obie próbki pochodziły z tego samego rozkładu, możliwe jest otrzymanie konfiguracji zawierającej małą liczbę serii, a więc np. tego typu, jak w (2) i (3). Na szczęście, jak się okazuje, jest to mało prawdopodobne. Druga uwaga dotyczy interpretacji słów duża bądź mała liczba serii. Co to, tak naprawdę, znaczy? Owszem, w rozważanym przykładzie maksymalna możliwa liczba serii wynosi 9, ale czy liczba serii równa 6, jak w przypadku (1), oznacza już dużą czy wciąż jeszcze małą liczbę serii? Do odpowiedzi na to pytanie posłuży nam rachunek prawdopodobieństwa.

Niech 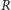 oznacza liczbę serii występujących w rozważanym ciągu symboli. Oczywiście, liczba serii nie może być mniejsza niż liczba różnych symboli w ciągu, a zarazem większa niż łączna liczba obserwacji w obu próbkach, tzn.
oznacza liczbę serii występujących w rozważanym ciągu symboli. Oczywiście, liczba serii nie może być mniejsza niż liczba różnych symboli w ciągu, a zarazem większa niż łączna liczba obserwacji w obu próbkach, tzn. 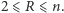 Jako kryterium rozdzielające małą i dużą liczbę serii przyjmiemy pewną wartość krytyczną
Jako kryterium rozdzielające małą i dużą liczbę serii przyjmiemy pewną wartość krytyczną 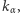 czyli taką największą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy (o braku różnic między rozkładami obu próbek) - zachodzi
czyli taką największą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy (o braku różnic między rozkładami obu próbek) - zachodzi
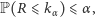 |
gdzie 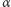 jest tzw. poziomem istotności, czyli przyjętym z góry ograniczeniem na prawdopodobieństwo odrzucenia hipotezy, gdy faktycznie jest ona prawdziwa (zwyczajowo przyjmowaną wartością poziomu istotności jest
jest tzw. poziomem istotności, czyli przyjętym z góry ograniczeniem na prawdopodobieństwo odrzucenia hipotezy, gdy faktycznie jest ona prawdziwa (zwyczajowo przyjmowaną wartością poziomu istotności jest 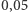 ).
).
Innymi słowy, policzywszy, ile serii 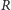 występuje w ciągu utworzonym z połączonych próbek oraz dysponując wartością krytyczną
występuje w ciągu utworzonym z połączonych próbek oraz dysponując wartością krytyczną 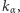 nasz test równości rozkładów wygląda następująco:
nasz test równości rozkładów wygląda następująco:
- jeśli
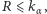 wówczas odrzucamy hipotezę o równości rozkładów,
wówczas odrzucamy hipotezę o równości rozkładów, - jeśli
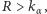 to nie mamy podstaw do odrzucenia weryfikowanej hipotezy.
to nie mamy podstaw do odrzucenia weryfikowanej hipotezy.
Pozostaje nam teraz wskazać metodę wyznaczania wartości krytycznych 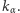 Pomocne będą w tym dwa twierdzenia.
Pomocne będą w tym dwa twierdzenia.
Twierdzenie 1. Niech 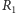 i
i 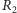 oznaczają, odpowiednio, liczbę serii obiektów pierwszego i drugiego rodzaju w ciągu utworzonym przez
oznaczają, odpowiednio, liczbę serii obiektów pierwszego i drugiego rodzaju w ciągu utworzonym przez 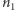 obiektów pierwszego rodzaju i
obiektów pierwszego rodzaju i 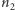 obiektów drugiego rodzaju. Wówczas, przy założeniu równości rozkładów obu próbek, zachodzi
obiektów drugiego rodzaju. Wówczas, przy założeniu równości rozkładów obu próbek, zachodzi
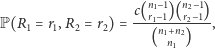 |
(4) |
gdzie 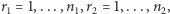 przy czym
przy czym 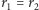 lub
lub 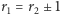 oraz
oraz 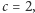 gdy
gdy 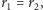 zaś
zaś 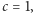 gdy
gdy 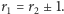
Dowód. Zakładając równość rozkładów obu próbek, wszystkie możliwe układy 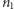 elementów pierwszego rodzaju i
elementów pierwszego rodzaju i 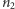 elementów drugiego rodzaju są tak samo prawdopodobne. Takich rozróżnialnych układów jest
elementów drugiego rodzaju są tak samo prawdopodobne. Takich rozróżnialnych układów jest 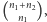 zatem mamy już mianownik wyrażenia (4). Aby otrzymać licznik, zauważmy, że liczba różnych sposobów otrzymania
zatem mamy już mianownik wyrażenia (4). Aby otrzymać licznik, zauważmy, że liczba różnych sposobów otrzymania 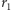 serii z
serii z 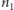 obiektów pierwszego typu wynosi
obiektów pierwszego typu wynosi 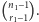 Łatwo to dostrzec, wyobrażając sobie, że mamy rozmieścić
Łatwo to dostrzec, wyobrażając sobie, że mamy rozmieścić 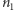 białych kul w
białych kul w 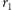 komórkach w ten sposób, aby w każdej komórce znalazła się przynajmniej jedna kula. Można to zrealizować, na przykład, tak, że między ustawione w linii białe kule wstawia się
komórkach w ten sposób, aby w każdej komórce znalazła się przynajmniej jedna kula. Można to zrealizować, na przykład, tak, że między ustawione w linii białe kule wstawia się 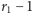 przegród. Ponieważ mamy
przegród. Ponieważ mamy 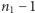 możliwych miejsc, w które można wstawić przegrodę, otrzymujemy owe
możliwych miejsc, w które można wstawić przegrodę, otrzymujemy owe 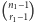 potencjalnych układów.
potencjalnych układów.
To samo rozumowanie można, oczywiście, powtórzyć wobec 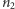 obiektów drugiego rodzaju, które tworzą
obiektów drugiego rodzaju, które tworzą 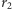 serii. Wobec tego łączna liczba rozróżnialnych układów, zaczynająca się serią obiektów pierwszego rodzaju, wynosi
serii. Wobec tego łączna liczba rozróżnialnych układów, zaczynająca się serią obiektów pierwszego rodzaju, wynosi 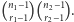 Tyle samo układów otrzymamy, gdy ciąg serii rozpoczyna seria obiektów drugiego rodzaju. Ponieważ zaś serie obiektów pierwszego i drugiego rodzaju muszą występować na przemian, w konsekwencji musi zachodzić
Tyle samo układów otrzymamy, gdy ciąg serii rozpoczyna seria obiektów drugiego rodzaju. Ponieważ zaś serie obiektów pierwszego i drugiego rodzaju muszą występować na przemian, w konsekwencji musi zachodzić 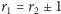 albo
albo 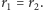 Jeśli zachodzi
Jeśli zachodzi 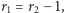 to ciąg serii rozpoczyna seria obiektów drugiego rodzaju. Gdy
to ciąg serii rozpoczyna seria obiektów drugiego rodzaju. Gdy 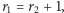 to jako pierwsza występuje seria obiektów pierwszego rodzaju. Natomiast w sytuacji, gdy
to jako pierwsza występuje seria obiektów pierwszego rodzaju. Natomiast w sytuacji, gdy 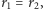 jako pierwsza w ciągu może pojawić się zarówno seria pierwszego, jak i drugiego rodzaju, co sprawia, że liczbę rozróżnialnych układów należy podwoić. W ten sposób otrzymujemy licznik wyrażenia (4), co kończy dowód.
jako pierwsza w ciągu może pojawić się zarówno seria pierwszego, jak i drugiego rodzaju, co sprawia, że liczbę rozróżnialnych układów należy podwoić. W ten sposób otrzymujemy licznik wyrażenia (4), co kończy dowód.
Twierdzenie 2. Przy założeniu równości rozkładów obu próbek rozkład łącznej liczby serii 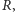 w ciągu utworzonym przez
w ciągu utworzonym przez 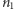 obiektów pierwszego rodzaju i
obiektów pierwszego rodzaju i 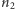 obiektów drugiego rodzaju, jest dany wzorem
obiektów drugiego rodzaju, jest dany wzorem
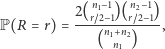 |
(5) |
gdy  jest parzyste oraz
jest parzyste oraz
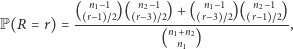 |
(6) |
gdy  jest nieparzyste. Wzory te są prawdziwe dla
jest nieparzyste. Wzory te są prawdziwe dla 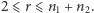
Dowód. Powyższe twierdzenie wynika bezpośrednio z twierdzenia 1. Istotnie, jeśli  jest parzyste, to liczba serii obu rodzajów obiektów musi być taka sama, tzn.
jest parzyste, to liczba serii obu rodzajów obiektów musi być taka sama, tzn. 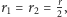 co po podstawieniu do wzoru (4) daje (5). Natomiast, gdy
co po podstawieniu do wzoru (4) daje (5). Natomiast, gdy  jest nieparzyste, wówczas
jest nieparzyste, wówczas 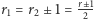 i sumując oba te przypadki, na mocy (4) otrzymujemy (6).
i sumując oba te przypadki, na mocy (4) otrzymujemy (6).
Jak można wykorzystać powyższe wyniki we wnioskowaniu statystycznym? Wyobraźmy sobie, na przykład, że w pewnym supermarkecie postanowiono zbadać, czy istnieje związek między ceną produktów chemicznych a czasem, jaki klient poświęca, oglądając dany produkt, zanim podejmie decyzję o zakupie. W tym celu zarejestrowano długość czasu, przez jaki klienci oglądali jeden z dwóch środków czyszczących, sprzedawanych w opakowaniach o tej samej pojemności, ale różniących się ceną. Losowo wybrane wyniki zawiera poniższa tabela.

Ustawmy wszystkie pomiary w ciąg rosnący, pamiętając przy tym, do której grupy cenowej należy każdy z nich. Jeśli teraz pominiemy wartości pomiarów, a pozostawimy tylko etykiety wskazujące, czy dany pomiar związany był z produktem droższym (ozn. 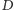 ), czy tańszym (ozn.
), czy tańszym (ozn. 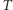 ), otrzymamy następujący ciąg symboli:
), otrzymamy następujący ciąg symboli:
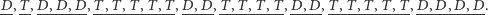 |
Jak widać, ciąg ten zawiera 9 serii. Korzystając z twierdzenia 2, możemy łatwo obliczyć prawdopodobieństwa możliwych wartości liczby serii w 27-elementowym ciągu otrzymanym z 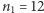 elementów pierwszego rodzaju i
elementów pierwszego rodzaju i 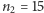 elementów drugiego rodzaju - przybliżone wyniki znajdują się na tutaj (zachęcam Czytelnika do skontrolowania choćby kilku z nich).
elementów drugiego rodzaju - przybliżone wyniki znajdują się na tutaj (zachęcam Czytelnika do skontrolowania choćby kilku z nich).
Sumując wartości obliczonych prawdopodobieństw, dostaniemy 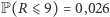 oraz
oraz 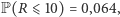 z czego wynika, że np. dla poziomu istotności
z czego wynika, że np. dla poziomu istotności 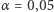 wartość krytyczna testu wynosi
wartość krytyczna testu wynosi 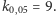 A ponieważ w przeprowadzonym doświadczeniu otrzymaliśmy 9 serii, na mocy opisanej powyżej reguły decyzyjnej odrzucamy hipotezę o równości rozkładów. Zatem rozkłady odpowiadające badanym produktom różnią się, co oznacza, że istnieje związek między ceną produktów chemicznych a czasem, jaki klient poświęca, oglądając dany produkt, zanim podejmie decyzję o jego zakupie.
A ponieważ w przeprowadzonym doświadczeniu otrzymaliśmy 9 serii, na mocy opisanej powyżej reguły decyzyjnej odrzucamy hipotezę o równości rozkładów. Zatem rozkłady odpowiadające badanym produktom różnią się, co oznacza, że istnieje związek między ceną produktów chemicznych a czasem, jaki klient poświęca, oglądając dany produkt, zanim podejmie decyzję o jego zakupie.
Test równości rozkładów nie jest jedynym interesującym testem wykorzystującym pojęcie serii. Innym ciekawym narzędziem statystycznym jest test losowości.
Wyobraźmy sobie, że obserwujemy wchodzących do kina, notując płeć kolejnych osób. Załóżmy, że ostatnie 10 osób wygenerowało następujący ciąg: 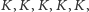
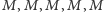 gdzie symbole
gdzie symbole 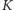 i
i 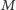 oznaczają, odpowiednio, kobietę i mężczyznę. Tego typu ciąg trudno byłoby uznać za losowy, gdyż odpowiadałby on sytuacji, w której do kina wchodzą najpierw kobiety, a potem mężczyźni. Równie mało losowy byłby ciąg
oznaczają, odpowiednio, kobietę i mężczyznę. Tego typu ciąg trudno byłoby uznać za losowy, gdyż odpowiadałby on sytuacji, w której do kina wchodzą najpierw kobiety, a potem mężczyźni. Równie mało losowy byłby ciąg 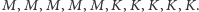 W obu przypadkach ciągi zawierałyby jedynie po dwie serie. A zatem mała liczba serii wskazywałaby na duże zgrupowanie podobnych obiektów, co kłóciłoby się z losowością. Zwróćmy jednak uwagę, iż diametralnie inny ciąg:
W obu przypadkach ciągi zawierałyby jedynie po dwie serie. A zatem mała liczba serii wskazywałaby na duże zgrupowanie podobnych obiektów, co kłóciłoby się z losowością. Zwróćmy jednak uwagę, iż diametralnie inny ciąg: 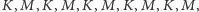 byłoby równie trudno uznać za losowy. Sugerowałby on bowiem, iż do kina wchodziły pary. Tak więc tym razem duża liczba serii (w rozważanym ciągu jest ich 10) także wskazywałaby na brak losowości, jakkolwiek innej natury, niż to miało miejsce w poprzednich przykładach.
byłoby równie trudno uznać za losowy. Sugerowałby on bowiem, iż do kina wchodziły pary. Tak więc tym razem duża liczba serii (w rozważanym ciągu jest ich 10) także wskazywałaby na brak losowości, jakkolwiek innej natury, niż to miało miejsce w poprzednich przykładach.

Naturalne pytanie, jakie nasuwa się w tym miejscu, brzmi zatem: Kiedy dany ciąg możemy uznać za losowy? Na tak postawione pytanie łatwiej odpowiedzieć przez dopełnienie, określając, kiedy ciąg nie jest losowy. Mianowicie, powszechnie przyjmuje się, że ciąg jest nielosowy, jeśli tworzy jakąś strukturę. Takie określenie interesującego nas pojęcia może nie wszystkich zadowala, ale jest dość intuicyjne. O ile jednak stosunkowo łatwo analizować w tym kontekście ciągi krótkie i wyraźnie ustrukturyzowane, jak choćby te wskazane powyżej, do badania losowości dowolnych ciągów przydają się rozmaite metody statystyczne. Należy do nich również test losowości wykorzystujący liczbę serii. Tym razem jednak, w przeciwieństwie do omawianego wcześniej testu równości dwóch rozkładów, odrzucamy hipotezę o losowości, jeśli liczba serii jest zarówno zbyt mała, jak i zbyt duża. A to oznacza, że do podjęcia decyzji potrzebne są dwie wartości krytyczne: dolna 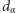 i górna
i górna 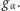 Wyznaczamy je ze wzorów podanych w twierdzeniu 2, przy czym
Wyznaczamy je ze wzorów podanych w twierdzeniu 2, przy czym 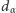 oznacza taką największą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy o losowości - zachodzi
oznacza taką największą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy o losowości - zachodzi
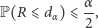 |
natomiast 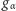 oznacza taką najmniejszą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy o losowości - zachodzi
oznacza taką najmniejszą liczbę całkowitą, dla której - przy założeniu prawdziwości testowanej hipotezy o losowości - zachodzi
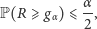 |
gdzie 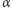 jest przyjętym poziomem istotności.
jest przyjętym poziomem istotności.
Dysponując tak wyznaczonymi wartościami krytycznymi oraz policzywszy, ile serii 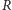 występuje w badanym ciągu, nasz test losowości przebiega następująco:
występuje w badanym ciągu, nasz test losowości przebiega następująco:
- jeśli
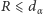 lub
lub 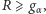 wówczas odrzucamy hipotezę o losowości ciągu obserwacji,
wówczas odrzucamy hipotezę o losowości ciągu obserwacji, - jeśli
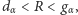 to nie mamy podstaw do odrzucenia weryfikowanej hipotezy.
to nie mamy podstaw do odrzucenia weryfikowanej hipotezy.
Zachęcamy Czytelników, aby spróbowali zbadać, czy ciąg wyników meczów rozegranych przez Federera i Nadala, od którego rozpoczęliśmy nasze rozważania, jest losowy.
Wspomnijmy jeszcze tylko, że oprócz liczby serii ciekawe może być również to, jak długie są poszczególne serie, jaki jest rozmiar najdłuższej serii, itd. Tego typu informacje mogą także okazać się przydatne do testowania losowości.
Na zakończenie podkreślmy jeszcze jedną, niezwykle ważną cechę omawianych testów serii, jaką jest ich nieparametryczność. Pojęcie to nieco lepiej oddaje język angielski poprzez określenie distribution-free, oznaczające procedurę, która nie zależy od rozkładu badanej próbki. W statystyce jest to bardzo pożądana własność, otwierająca szerokie pole do potencjalnych zastosowań danej procedury, wolnej od rozmaitych, często kłopotliwych ograniczeń.
