O rybach i ufności
W poprzednim numerze Delty przedstawiliśmy zgrabną metodę szacowania liczby ryb pływających w stawie. Przypomnijmy doświadczenie, na którym ta metoda się opierała: najpierw łowimy rybkę, potem rysujemy jej kreskę na ogonku, następnie na kartce zapisujemy liczbę kresek, jakie widzimy na ogonku trzymanej w ręce rybki, po czym wrzucamy ją z powrotem do stawu i całą procedurę powtarzamy 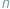 razy.
razy.

Niech  będzie (nieznaną) liczbą ryb pływających w jeziorze. Poprzednio wykazaliśmy, że prawdopodobieństwo uzyskania na kartce konkretnego ciągu
będzie (nieznaną) liczbą ryb pływających w jeziorze. Poprzednio wykazaliśmy, że prawdopodobieństwo uzyskania na kartce konkretnego ciągu  wynosi
wynosi 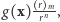 gdzie
gdzie  jest liczbą jedynek w tym ciągu (tzn. liczbą różnych, złowionych przez nas ryb), zaś
jest liczbą jedynek w tym ciągu (tzn. liczbą różnych, złowionych przez nas ryb), zaś 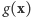 jest czynnikiem niezależnym od
jest czynnikiem niezależnym od 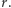 Wynika stąd, że
Wynika stąd, że 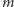 jest statystyką dostateczną i zawiera całą dostępną nam informację o
jest statystyką dostateczną i zawiera całą dostępną nam informację o 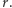 Niech
Niech 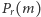 oznacza prawdopodobieństwo wyłowienia dokładnie
oznacza prawdopodobieństwo wyłowienia dokładnie  różnych ryb. Nietrudno przekonać się, że
różnych ryb. Nietrudno przekonać się, że 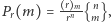 gdzie
gdzie 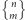 jest liczbą podziałów zbioru
jest liczbą podziałów zbioru 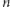 -elementowego na
-elementowego na  rozłącznych podzbiorów (na tyle sposobów możemy złowić
rozłącznych podzbiorów (na tyle sposobów możemy złowić 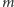 różnych ryb przy
różnych ryb przy 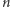 połowach). Wybierzmy teraz "małą" liczbę
połowach). Wybierzmy teraz "małą" liczbę 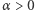 (na przykład
(na przykład 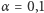 ) i zdefiniujmy przedział
) i zdefiniujmy przedział ![[m1(r),m2(r)]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/19x-bd25e1424a45d4ecaf63fcb3a79d19c4aae4cd20-im-33,33,33-FF,FF,FF.gif) w następujący sposób:
w następujący sposób:


Konstrukcja przedziału ufności dla 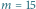 i
i 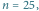 na poziomie
na poziomie  Pionowe linie są przedziałami o prawdopodobieństwie (co najmniej) 90%. Przedział dla
Pionowe linie są przedziałami o prawdopodobieństwie (co najmniej) 90%. Przedział dla 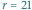 został wyróżniony tylko dla ułatwienia objaśnień. Poziomy odcinek jest przedziałem ufności.
został wyróżniony tylko dla ułatwienia objaśnień. Poziomy odcinek jest przedziałem ufności.
Wynika stąd, że
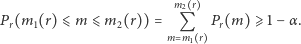 |
(1) |
Nierówność (1) mówi o tym, że z "dużym prawdopodobieństwem"  losowa wielkość
losowa wielkość  należy do przedziału
należy do przedziału ![[m1(r),m2(r)],](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/4x-c5e5cc7db510a53e5d95e986e3da65891b90fe07-im-33,33,33-FF,FF,FF.gif) który zależy od nieznanego
który zależy od nieznanego 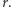 Na rysunku pionowe odcinki przedstawiają przedziały obliczone dla
Na rysunku pionowe odcinki przedstawiają przedziały obliczone dla 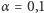 i różnych wartości
i różnych wartości  (od 1 do 50). Przykładowo, dla
(od 1 do 50). Przykładowo, dla 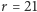 mamy
mamy 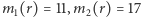 i
i 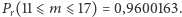
Przedstawione zależności wynikają z patrzenia na nasz rysunek pionowo, czyli dla różnych, ale ustalonych wartości 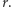 To jest punkt widzenia probabilisty. Punkt widzenia statystyka jest poziomy. Rozpatrujemy ustaloną (bo zaobserwowaną) wartość
To jest punkt widzenia probabilisty. Punkt widzenia statystyka jest poziomy. Rozpatrujemy ustaloną (bo zaobserwowaną) wartość 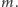 Zdefiniujmy dwie zależne od
Zdefiniujmy dwie zależne od 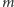 liczby "na osi poziomej":
liczby "na osi poziomej":

Na przykład, dla 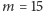 mamy
mamy 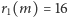 i
i 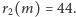 Przedział
Przedział ![|[16,44]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/8x-8c312a3c509e48a0459ccf3d22013cd06ae1c3d5-im-33,33,33-FF,FF,FF.gif) na "wysokości"
na "wysokości" 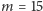 jest na rysunku wyróżniony.
jest na rysunku wyróżniony.
Doszliśmy teraz do najważniejszego miejsca naszych rozważań. Chwila zastanowienia prowadzi do wniosku, że następujące dwa warunki są równoważne:

W istocie, wynika to z definicji 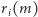 i z faktu, że obie funkcje
i z faktu, że obie funkcje 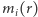 są niemalejące, co nietrudno sprawdzić. Wynika stąd zatem, że dla każdego
są niemalejące, co nietrudno sprawdzić. Wynika stąd zatem, że dla każdego 
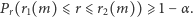 |
(2) |
Nierówność (2) mówi o tym, że dla dowolnego 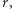 przedział
przedział ![|[r1(m),r2(m)]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/7x-06b7ec8c36af20c373d99f58281e4a9d90b753af-im-33,33,33-FF,FF,FF.gif) zawiera nieznaną liczbę
zawiera nieznaną liczbę  z dużym prawdopodobieństwem. Ten przedział możemy obliczyć, bo znamy
z dużym prawdopodobieństwem. Ten przedział możemy obliczyć, bo znamy 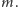 Wspaniale! Wróćmy do naszych przykładowych danych, które pojawiły się na początku artykułu. Dla
Wspaniale! Wróćmy do naszych przykładowych danych, które pojawiły się na początku artykułu. Dla 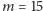 (i ustalonego
(i ustalonego 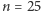 ), przypomnijmy,
), przypomnijmy, ![|[r (m),r (m)] = [16,44]. 1 2](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/12x-06b7ec8c36af20c373d99f58281e4a9d90b753af-im-33,33,33-FF,FF,FF.gif) A więc wydaje się, że następujące stwierdzenie jest zgodne z tym, co było powiedziane.
A więc wydaje się, że następujące stwierdzenie jest zgodne z tym, co było powiedziane.
): Przedział ![[16,44]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/1x-5e4b06fdedae4f5375882fde447409cd58223070-im-33,33,33-FF,FF,FF.gif) zawiera nieznaną liczbę
zawiera nieznaną liczbę  z prawdopodobieństwem co najmniej
z prawdopodobieństwem co najmniej 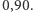
Ale, ale, chyba się zagalopowaliśmy. Jeśli liczba  nie jest zmienną losową, to powyższe zdanie jest bezsensowne. Przedział
nie jest zmienną losową, to powyższe zdanie jest bezsensowne. Przedział ![[16,44]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/2x-1e562bf2ce4d99c324cafb56de10f640aa26fd7c-im-33,33,33-FF,FF,FF.gif) albo zawiera
albo zawiera 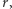 albo nie. Jak się jezioro osuszy, to się wyjaśni. Bez osuszania jeziora musimy nasz wniosek sformułować inaczej.
albo nie. Jak się jezioro osuszy, to się wyjaśni. Bez osuszania jeziora musimy nasz wniosek sformułować inaczej.
(: Przedział ![[16,44]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/1x-9152f9e2523baab2a2323d2adf1c6f08c55aec92-im-33,33,33-FF,FF,FF.gif) jest przedziałem ufności dla nieznanej liczby
jest przedziałem ufności dla nieznanej liczby  na poziomie ufności
na poziomie ufności 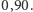
Jeśli o prawdopodobieństwie nie możemy mówić, to zastępujemy termin "prawdopodobieństwo" terminem "ufność". Matematyczną definicją przedziału ufności jest nierówność (2). Kłopot w tym, że prawdopodobieństwo we wzorze (2) opisuje niepewność wyniku doświadczenia, w tym przypadku wyłowienia 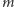 różnych ryb, przed wykonaniem doświadczenia (przed połowem). Jak więc interpretować przedział
różnych ryb, przed wykonaniem doświadczenia (przed połowem). Jak więc interpretować przedział ![[16,44]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/2x-886eb755e75c6b14717958cc08ebc088a33c6e8c-im-33,33,33-FF,FF,FF.gif) obliczony po wyłowieniu
obliczony po wyłowieniu 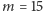 ryb?
ryb?
- Przedział ufności na poziomie
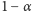 jest to przedział obliczony na podstawie wyniku doświadczenia losowego w taki sposób, że jeśliby powtarzać doświadczenie wielokrotnie, to dla przynajmniej
jest to przedział obliczony na podstawie wyniku doświadczenia losowego w taki sposób, że jeśliby powtarzać doświadczenie wielokrotnie, to dla przynajmniej 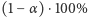 doświadczeń, przedział obliczony tą samą metodą zawierałby nieznany parametr.
doświadczeń, przedział obliczony tą samą metodą zawierałby nieznany parametr.
Zwróćmy uwagę, jaką rolę w interpretacji przedziału ufności odgrywają zdania warunkowe i tryb przypuszczający. Jest to charakterystyczny dla Statystyka sposób myślenia - po wykonaniu doświadczenia losowego zastanawia się on: "z jakim prawdopodobieństwem to czy tamto by się mogło zdarzyć, gdyby nie to, że już się zdarzyło".
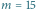 i
i 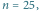 na poziomie
na poziomie 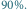 Pionowe linie są przedziałami o prawdopodobieństwie (co najmniej) 90%. Przedział dla
Pionowe linie są przedziałami o prawdopodobieństwie (co najmniej) 90%. Przedział dla 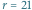 został wyróżniony tylko dla ułatwienia objaśnień. Poziomy odcinek jest przedziałem ufności.
został wyróżniony tylko dla ułatwienia objaśnień. Poziomy odcinek jest przedziałem ufności.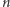 -elementowego na
-elementowego na  rozłącznych podzbiorów nosi nazwę liczby Stirlinga II rodzaju. Można tę liczbę obliczyć przy użyciu wygodnej rekurencji. Prawdziwa jest zależność
rozłącznych podzbiorów nosi nazwę liczby Stirlinga II rodzaju. Można tę liczbę obliczyć przy użyciu wygodnej rekurencji. Prawdziwa jest zależność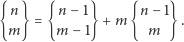
![[3,141592653589793238461, 3,141592653589793238462]](/math/temat/matematyka/rachunek_prawdopodobienstwa/statystyka/2017/07/29/O_rybach_i_ufnosci/1x-c9c2d2bee4f8d7bb967b6ceee12bfff971ff01b7-dm-33,33,33-FF,FF,FF.gif)
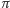 z prawdopodobieństwem co najmniej
z prawdopodobieństwem co najmniej 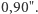 Albo zawiera, albo nie. Chwilowo mogę nie wiedzieć, która z alternatywnych możliwości zachodzi, ale o żadnym prawdopodobieństwie nie można mówić! Jak się zajrzy do Wikipedii, to się wyjaśni.
Albo zawiera, albo nie. Chwilowo mogę nie wiedzieć, która z alternatywnych możliwości zachodzi, ale o żadnym prawdopodobieństwie nie można mówić! Jak się zajrzy do Wikipedii, to się wyjaśni.