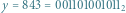Czułość funkcji logicznych (II)
W pierwszej części artykułu (Delta 7/2020) omówiliśmy pojęcia funkcji logicznej, jej czułości i przedstawiliśmy, na razie bez dowodów, pewne związane z nimi twierdzenia, udowodnione w pracy [1]. Celem drugiej części jest przedstawienie owych dowodów w wersji nieco uproszczonej w stosunku do oryginalnej pracy [1], ale wciąż wymagającej znajomości podstaw algebry liniowej, w tym mnożenia macierzy i pewnej wiedzy o wymiarze przestrzeni liniowej.
Na przykład w 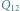 połączone będą między innymi
połączone będą między innymi
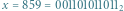 i
i
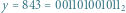
Niech 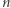 będzie dowolną dodatnią liczbą całkowitą i niech
będzie dowolną dodatnią liczbą całkowitą i niech 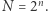 Zapiszmy elementy zbioru
Zapiszmy elementy zbioru 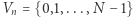 w układzie dwójkowym (uzupełniając w miarę potrzeby nieznaczącymi początkowymi zerami, tak by każda liczba miała dokładnie
w układzie dwójkowym (uzupełniając w miarę potrzeby nieznaczącymi początkowymi zerami, tak by każda liczba miała dokładnie 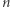 cyfr) i przedstawmy je graficznie w ten sposób, że elementy
cyfr) i przedstawmy je graficznie w ten sposób, że elementy 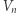 (zwane wierzchołkami) będą punktami, a odcinki (zwane krawędziami) połączą pary wierzchołków różniące się w układzie dwójkowym tylko jedną cyfrą. Uzyskany graf nazwiemy n-wymiarową kostką
(zwane wierzchołkami) będą punktami, a odcinki (zwane krawędziami) połączą pary wierzchołków różniące się w układzie dwójkowym tylko jedną cyfrą. Uzyskany graf nazwiemy n-wymiarową kostką 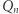 (nazwa wiąże się niewątpliwie z podobieństwem
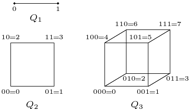
(nazwa wiąże się niewątpliwie z podobieństwem 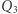 do szkieletu sześcianu, czyli standardowej kostki do gry). Spróbujmy przezwyciężyć fakt, że bezpośrednio odczuwamy istnienie tylko trzech wymiarów, spoglądając na kostki rekurencyjnie:
do szkieletu sześcianu, czyli standardowej kostki do gry). Spróbujmy przezwyciężyć fakt, że bezpośrednio odczuwamy istnienie tylko trzech wymiarów, spoglądając na kostki rekurencyjnie: 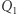 to dwa punkty połączone odcinkiem,
to dwa punkty połączone odcinkiem, 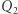 to dwa odcinki, np. dolny i górny, połączone dwiema pionowymi krawędziami,
to dwa odcinki, np. dolny i górny, połączone dwiema pionowymi krawędziami, 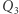 to dwie kopie
to dwie kopie 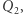 np. dolny i górny kwadrat, połączone czterema pionowymi krawędziami,
np. dolny i górny kwadrat, połączone czterema pionowymi krawędziami,  ,
, 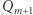 to dwie kopie
to dwie kopie 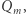 połączone
połączone 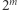 krawędziami i tak dalej.
krawędziami i tak dalej.
Zapowiedziane pod koniec pierwszej części twierdzenie (jeśli ponad połowę wierzchołków 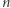 -wymiarowej kostki zajmują mrówki, to któraś z nich ma co najmniej
-wymiarowej kostki zajmują mrówki, to któraś z nich ma co najmniej 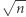 sąsiadek) możemy sformułować w następujący równoważny sposób.
sąsiadek) możemy sformułować w następujący równoważny sposób.
Twierdzenie (Huang). Jeśli wyróżnimy niektóre wierzchołki  -wymiarowej kostki
-wymiarowej kostki 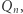 czyli wybierzemy podzbiór
czyli wybierzemy podzbiór 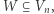 przy zachowaniu warunku, że każdy element
przy zachowaniu warunku, że każdy element 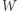 ma mieć mniej niż
ma mieć mniej niż 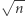 sąsiadów należących do
sąsiadów należących do 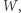 to wyróżnione wierzchołki stanowić będą co najwyżej połowę wszystkich wierzchołków kostki, czyli
to wyróżnione wierzchołki stanowić będą co najwyżej połowę wszystkich wierzchołków kostki, czyli 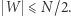
W terminologii teorii grafów twierdzenie Huanga brzmi:
Twierdzenie. każdy indukowany podgraf 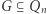 spełnia
spełnia 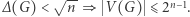
Dużo krócej, ale trzeba wpierw wyjaśnić, że 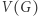 to zbiór wierzchołków grafu
to zbiór wierzchołków grafu 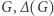 to największy stopień wierzchołka (stopień to z kolei liczba krawędzi o końcu w danym wierzchołku), a podgraf indukowany oznacza pewne wierzchołki wraz ze wszystkimi łączącymi je krawędziami
to największy stopień wierzchołka (stopień to z kolei liczba krawędzi o końcu w danym wierzchołku), a podgraf indukowany oznacza pewne wierzchołki wraz ze wszystkimi łączącymi je krawędziami 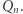
- Cały artykuł dostępny jest w wersji do druku: (533 KB)
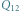 połączone będą między innymi
połączone będą między innymi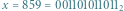 i
i