Czułość funkcji logicznych (I)
Najpierw jednak spróbujmy wyjaśnić, dlaczego poważni specjaliści chcieli w ogóle rozważać tak (pozornie) niepoważne zagadnienie...
Zacznijmy od dwóch powiązanych pytań:
- Czy pięć mrówek może zająć pięć różnych wierzchołków sześcianu w taki sposób, by każda miała najwyżej jedną sąsiadkę (powiemy, że mrówki sąsiadują, gdy siedzą na końcach pewnej krawędzi sześcianu)?
- Czy pięć mrówek może zająć pięć różnych wierzchołków sześcianu w taki sposób, by każda miała najwyżej dwie sąsiadki?
Czytelnik, który bez trudu rozprawił się z tymi zagadkami, zdziwi się zapewne, że rozwiązanie tego problemu (co prawda nie tylko dla zwykłej trójwymiarowej kostki, ale w dowolnie wielu wymiarach, o czym później), przedstawione przez Hao Huanga w lipcu 2019 roku, zostało przez społeczność informatyków-teoretyków przyjęte z niemałym entuzjazmem jako rozstrzygnięcie ważnej hipotezy, postawionej prawie 30 lat wcześniej.
Najpierw jednak spróbujmy wyjaśnić, dlaczego poważni specjaliści chcieli w ogóle rozważać tak (pozornie) niepoważne zagadnienie.
Funkcje boolowskie
W klasycznej logice rozważa się zdania, którym przypisuje się wartości logiczne "prawda" lub "fałsz", oraz operatory logiczne, z których najczęściej używane widnieją obok. Zauważmy, że używanie liczb zamiast wartości logicznych (najczęstsze jest utożsamianie prawdy z jednością, a fałszu z zerem) może znacznie uprościć zapis. Zamiast mówić: koniunkcja 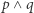 (czytaj "
(czytaj " 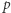 i
i 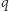 ") to zdanie, które jest prawdziwe, gdy oba jego człony są prawdziwe, fałszywe zaś w każdym innym przypadku, wystarczy napisać "
") to zdanie, które jest prawdziwe, gdy oba jego człony są prawdziwe, fałszywe zaś w każdym innym przypadku, wystarczy napisać " 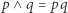 ".
".
Ogólnie mówiąc, 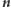 -argumentową funkcją boolowską (lub logiczną) będziemy nazywali każdą funkcję
-argumentową funkcją boolowską (lub logiczną) będziemy nazywali każdą funkcję 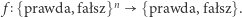 Mówiąc nie wiem, czy zdążę dziś pójść na (p)ocztę, do (s)klepu i naprawić (r)ower, ale chcę zrobić chociaż dwie z tych rzeczy, możemy zapisać funkcję logiczną opisującą, czy ten plan został wykonany:
Mówiąc nie wiem, czy zdążę dziś pójść na (p)ocztę, do (s)klepu i naprawić (r)ower, ale chcę zrobić chociaż dwie z tych rzeczy, możemy zapisać funkcję logiczną opisującą, czy ten plan został wykonany:
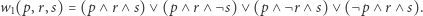 |
Analogiczny zapis możemy zastosować do każdej funkcji boolowskiej - po prostu spośród wszystkich 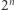 układów wartości logicznych argumentów wybieramy te, dla których nasze zdanie złożone jest prawdziwe. Czasami jednak funkcję można zapisać krócej, np. tak:
układów wartości logicznych argumentów wybieramy te, dla których nasze zdanie złożone jest prawdziwe. Czasami jednak funkcję można zapisać krócej, np. tak:
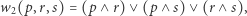 |
uwzględniając, że zbiór 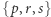 ma trzy dwuelementowe podzbiory, lub tak:
ma trzy dwuelementowe podzbiory, lub tak:
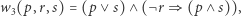 |
co nawet można dość zrozumiale wypowiedzieć: zajrzę na pocztę lub do sklepu, ale jeśli nie naprawię roweru, to pójdę i tu, i tu. (Czy dla Czytelnika jest oczywiste, że to sformułowanie jest równoważne poprzedniemu? Dla autora nie całkiem, za każdym razem musi się on chwilę zastanowić.)
Skąd jednak wiadomo, że to rzeczywiście ciągle ta sama funkcja logiczna, czyli że formuły 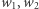 i
i 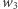 są faktycznie równoważne? Z pewnością można podstawić po kolei wszystkie
są faktycznie równoważne? Z pewnością można podstawić po kolei wszystkie 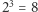 układów wartości zmiennych
układów wartości zmiennych 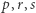 należących do {0,1} i sprawdzić, czy dla każdej z formuł dostajemy jednakowe wyniki. Inny sposób wykorzystuje przedstawione wyżej na marginesie algebraiczne definicje operatorów logicznych. Na przykład
należących do {0,1} i sprawdzić, czy dla każdej z formuł dostajemy jednakowe wyniki. Inny sposób wykorzystuje przedstawione wyżej na marginesie algebraiczne definicje operatorów logicznych. Na przykład
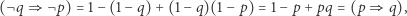 |
a zatem zdania 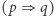 i
i 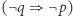 są równoważne. Podobnie wyznaczymy
są równoważne. Podobnie wyznaczymy
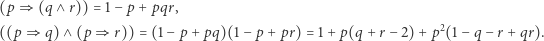
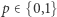 zachodzi
zachodzi 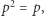 czyli
czyli
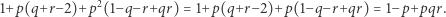 |
Zatem i tym razem mamy do czynienia z równoważnością
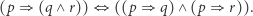 |
Cierpliwy Czytelnik lub odpowiednio zaprogramowany komputer może wyznaczyć wielomiany odpowiadające wyrażeniom 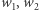 i
i 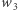 i stwierdzić, że wszystkie one są równe
i stwierdzić, że wszystkie one są równe 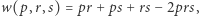 a to dowodzi równoważności tych wyrażeń.
a to dowodzi równoważności tych wyrażeń.
Dzięki redukcjom typu 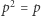 każda
każda 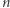 -argumentowa funkcja boolowska może być zapisana w postaci wielomianu
-argumentowa funkcja boolowska może być zapisana w postaci wielomianu  zmiennych, w którym nie występują wykładniki większe od 1. Różne wielomiany nie mogą definiować tej samej funkcji boolowskiej - wynika to z ogólnych własności wielomianów. Przez stopień funkcji boolowskiej, oznaczany przez
zmiennych, w którym nie występują wykładniki większe od 1. Różne wielomiany nie mogą definiować tej samej funkcji boolowskiej - wynika to z ogólnych własności wielomianów. Przez stopień funkcji boolowskiej, oznaczany przez 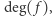 będziemy rozumieć stopień jej wielomianu, na przykład
będziemy rozumieć stopień jej wielomianu, na przykład 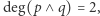
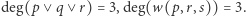
Czułość funkcji boolowskich
Starając się o kredyt, pan Kowalski rzetelnie wypełnił kwestionariusz z setką pytań. Otrzymał decyzję odmowną - bankowy analityk wyjaśnił swojemu przełożonemu, że odpowiedzi na pytania 14, 58 i 83 wskazują na skłonność klienta do nadmiernych wydatków. Pan Kowalski nigdy się jednak nie dowie, że dostałby kredyt, wystarczyłoby tylko, odpowiadając na jedno z tych trzech pytań, skłamać.
Decyzja podejmowana na podstawie kwestionariusza to pewna funkcja boolowska. W rzeczywistości nie na każde pytanie można odpowiedzieć tak lub nie, ale nie jest to silne ograniczenie, bo na przykład pytanie z tysiącem dopuszczalnych odpowiedzi można w zasadzie zastąpić dziesięcioma pytaniami binarnymi. To, że zmiana pojedynczego argumentu może zmienić wartość funkcji, jest przejawem zjawiska zwanego czułością.
Niech więc 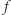 będzie
będzie  -argumentową funkcją boolowską, a
-argumentową funkcją boolowską, a 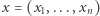 dowolnym elementem jej dziedziny. Czułością
dowolnym elementem jej dziedziny. Czułością 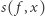 funkcji
funkcji 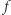 w punkcie
w punkcie  nazwiemy liczbę takich
nazwiemy liczbę takich 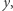 że
że 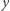 różni się od
różni się od  tylko na jednej współrzędnej, ale
tylko na jednej współrzędnej, ale 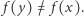 Czułością
Czułością 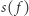 funkcji
funkcji 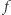 nazwiemy największą możliwą wartość czułości
nazwiemy największą możliwą wartość czułości 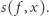
Przykład 1. Aby zdać egzamin, należy poprawnie odpowiedzieć na siedem z dziesięciu pytań.
- Alicja odpowiedziała poprawnie na 9 pytań i zdała. Czułość Alicji wynosi 0, gdyż zmiana jednej odpowiedzi nie może spowodować, że Alicja nie zda.
- Bartek odpowiedział dobrze na 7 pytań i zdał z trudem. Gdyby udzielił innej odpowiedzi na którekolwiek z tych pytań, nie zdałby. Jego czułość to 7.
- Czarek odpowiedział dobrze na 6 pytań i nie zdał, choć niewiele brakowało. Gdyby zaliczył choćby jedno z pozostałych 4 pytań, zdałby. Czułość Czarka to 4.
- Dagmara odpowiedziała dobrze na 5 pytań i nie zdała. Zmiana jednej odpowiedzi nic nie daje - poprawnych odpowiedzi będzie najwyżej 6, co nie wystarcza do pozytywnego wyniku. Czułość Dagmary wynosi 0.
Czułość całej funkcji to 7 i nietrudno zobaczyć, że wpływają na nią jedynie przypadki graniczne. Ogólnie, dla egzaminu z 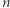 pytaniami i progiem zdania na poziomie
pytaniami i progiem zdania na poziomie 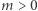 (oraz
(oraz 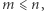 bo trudno żądać, by ktoś odpowiedział na ponad 100% pytań) czułość to większa z liczb
bo trudno żądać, by ktoś odpowiedział na ponad 100% pytań) czułość to większa z liczb 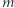 i
i 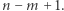
Przykład 2. Emil zaprosił na urodziny 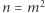 gości pochodzących z
gości pochodzących z 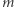 krajów (z każdego kraju dokładnie
krajów (z każdego kraju dokładnie 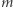 osób). Imprezę uzna za udaną, jeśli z każdego kraju przyjdzie co najmniej jeden gość (funkcją boolowską
osób). Imprezę uzna za udaną, jeśli z każdego kraju przyjdzie co najmniej jeden gość (funkcją boolowską 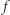 jest tu więc koniunkcja
jest tu więc koniunkcja 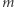 alternatyw po
alternatyw po 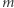 zmiennych w każdej, czyli funkcja stopnia
zmiennych w każdej, czyli funkcja stopnia 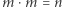 ). Rozważmy graniczne przypadki.
). Rozważmy graniczne przypadki.
- "Prawie nieudana" udana impreza ma miejsce wtedy, gdy z każdego kraju ktoś jest, ale z niektórych krajów tylko pojedyncze osoby, które mogą wyjść, psując urodziny. Tych pojedynczych osób jest nie więcej niż krajów, więc czułość nie przekracza
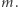
- "Prawie udana" nieudana impreza jest zaś wtedy, gdy z jakiegoś (ale tylko jednego) kraju nikt nie przyszedł. Wtedy czekamy, aż ktoś z
 zaproszonych z tego kraju gości jednak się pojawi - tu czułość wynosi
zaproszonych z tego kraju gości jednak się pojawi - tu czułość wynosi 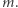
Ostatecznie czułość całej funkcji to 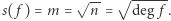
Po wprowadzeniu powyższych pojęć możemy już powiedzieć, że problem rozstrzygnięty przez Huanga pierwotnie wcale nie dotyczył mrówek na kostce:
Twierdzenie (Hipoteza o czułości - obecnie twierdzenie Huanga). Dla każdej funkcji boolowskiej 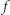 zachodzi nierówność
zachodzi nierówność 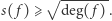
Związek funkcji boolowskich z kostkami jest dość prosty: podobnie jak zwykły sześcian możemy umieścić tak, by jego wierzchołkami były punkty 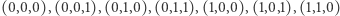 i
i 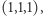 i powiedzieć, że jest to dziedzina trójargumentowej funkcji boolowskiej, tak możemy uważać złożone z zer i jedynek ciągi długości
i powiedzieć, że jest to dziedzina trójargumentowej funkcji boolowskiej, tak możemy uważać złożone z zer i jedynek ciągi długości 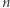 za współrzędne wierzchołków
za współrzędne wierzchołków  -wymiarowej kostki.
-wymiarowej kostki.
Wracając na razie do geometrii, możemy sformułować następujące twierdzenie:
Twierdzenie (Huang). Jeśli ponad połowę z 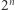 wierzchołków
wierzchołków 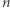 -wymiarowej kostki (czyli co najmniej
-wymiarowej kostki (czyli co najmniej 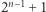 wierzchołków) zajmują mrówki, to co najmniej jedna z nich ma co najmniej
wierzchołków) zajmują mrówki, to co najmniej jedna z nich ma co najmniej 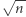 sąsiadek.
sąsiadek.
Dowód tego twierdzenia, wymagający jedynie znajomości podstaw algebry liniowej, w tym mnożenia macierzy, omówimy w kolejnej części artykułu, w następnym numerze. Powiemy wówczas również, jak z powyższego faktu wydedukować twierdzenie Huanga o czułości.