Nieskończoność
Rozmyślania o myślakach
W październikowym numerze Delty przedyskutowaliśmy hipotezę continuum i zaskakujące rozwiązanie problemu dotyczącego jej prawdziwości (o ile Czytelnik zgodzi się nazwać to rozwiązaniem). Na pytanie, czy istnieje nieskończony podzbiór zbioru liczb rzeczywistych, który nie jest równoliczny ze zbiorem liczb naturalnych ani ze zbiorem wszystkich liczb rzeczywistych (jest więc "większy" od zbioru liczb naturalnych, ale "mniejszy" od zbioru liczb rzeczywistych), odpowiedź nie brzmi "tak" ani "nie". Okazało się, że nie jest możliwe udowodnienie, że taki zbiór istnieje, ani że taki zbiór nie istnieje...

wikipedia
Paul Cohen (1934-2007)

wikipedia
Kurt Gödel (1906-1978)
Inaczej mówiąc, umiemy udowodnić, że nie da się udowodnić, iż taki zbiór istnieje (czego dokonał Paul Cohen). Ale też umiemy udowodnić, że nie da się udowodnić, że taki zbiór nie istnieje (tego dokonał wcześniej Kurt Gödel). Wszystko to przy założeniu, że same aksjomaty matematyki (czyli, powiedzmy, teorii zbiorów) są niesprzeczne.
Ale jak to możliwe? Czy nie jest przypadkiem tak, że każde matematyczne zdanie jest albo prawdziwe, albo nie? Spróbujemy się nad tym zastanowić w tym odcinku naszej nieskończonej przygody.
Zbliżamy się więc nieuchronnie do świata logiki. Ten świat wygodnie nam będzie zwiedzać razem z myślakami - stworzonkami wymyślonymi przez Raymonda Smullyana, które myślą w bardzo precyzyjny sposób. Będziemy zatem określać precyzyjnie coraz bardziej interesujące style myślenia i wnioskowania.
Zacznijmy od najprostszego typu myślaka. Myślak podstawowy po pierwsze wierzy we wszystkie tautologie. Tautologia to takie zdanie, które zawsze jest prawdziwe, niezależnie od okoliczności. Na przykład, jeśli  to dowolne zdanie logiczne, to zdanie "
to dowolne zdanie logiczne, to zdanie "  lub nie
lub nie 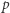 " jest tautologią. Myślak wierzy we wszystkie tego typu zdania. Po drugie, myślak podstawowy ma tę cechę, że jeśli wierzy w dowolne zdanie
" jest tautologią. Myślak wierzy we wszystkie tego typu zdania. Po drugie, myślak podstawowy ma tę cechę, że jeśli wierzy w dowolne zdanie 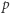 oraz w zdanie "z
oraz w zdanie "z 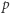 wynika
wynika 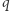 ", to również uwierzy w zdanie
", to również uwierzy w zdanie 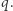
O myślaku powiemy, że jest sprzeczny, jeśli wierzy w pewne sprzeczne zdanie (np. w zdanie "nie jest prawdą, że  lub nie
lub nie 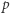 ", takie zdanie będziemy oznaczać
", takie zdanie będziemy oznaczać 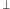 ). Zauważmy, że sprzeczny myślak podstawowy ma tę cechę, że wierzy absolutnie we wszystko. Rzeczywiście, skoro z fałszu wynika wszystko, dla dowolnego zdania
). Zauważmy, że sprzeczny myślak podstawowy ma tę cechę, że wierzy absolutnie we wszystko. Rzeczywiście, skoro z fałszu wynika wszystko, dla dowolnego zdania 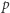 zdanie "jeśli
zdanie "jeśli 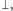 to
to 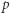 " jest tautologią, wiec myślak w nie wierzy. Skoro jednak wierzy również w
" jest tautologią, wiec myślak w nie wierzy. Skoro jednak wierzy również w  to wierzy także i w
to wierzy także i w 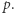 Myślaka będziemy nazywać zuchwałym, jeśli wierzy on w to, że nie jest sprzeczny.
Myślaka będziemy nazywać zuchwałym, jeśli wierzy on w to, że nie jest sprzeczny.
Warto jeszcze zwrócić uwagę na jedną kwestię. Nigdy do tej pory nie powiedzieliśmy, że jeśli myślak wierzy w jakieś zdanie 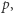 to wierzy, że w nie wierzy. To jest związane z pewną samoświadomością, której myślak podstawowy może nie posiadać. Ta cecha będzie nam jednak przydatna w dalszych rozważaniach. Dla każdego zdania
to wierzy, że w nie wierzy. To jest związane z pewną samoświadomością, której myślak podstawowy może nie posiadać. Ta cecha będzie nam jednak przydatna w dalszych rozważaniach. Dla każdego zdania  zdanie "myślak wierzy w
zdanie "myślak wierzy w 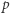 " oznaczmy jako
" oznaczmy jako 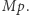
Powiemy na przykład, że myślak wie o myśleniu, jeśli dla każdych zdań 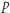 i
i 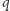 wierzy on, że jeśli uwierzy w
wierzy on, że jeśli uwierzy w  oraz w zdanie "jeśli
oraz w zdanie "jeśli 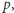 to
to 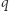 ", to uwierzy też w
", to uwierzy też w  Inaczej mówiąc, myślak wie o myśleniu, jeśli ma świadomość reguły rządzącej jego rozumowaniem. Formułując to jeszcze inaczej, myślak taki wierzy w każde zdanie postaci "jeśli
Inaczej mówiąc, myślak wie o myśleniu, jeśli ma świadomość reguły rządzącej jego rozumowaniem. Formułując to jeszcze inaczej, myślak taki wierzy w każde zdanie postaci "jeśli 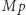 oraz
oraz 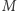 (jeśli
(jeśli 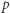 to
to 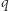 ), to
), to  ".
".
To jednak jeszcze nie wszystko. Dodajmy myślakom kolejny element samoświadomości. Powiemy, że myślak, który wie o myśleniu, jest normalny, jeśli za każdym razem, gdy wierzy w zdanie 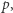 wierzy też w to, że wierzy w
wierzy też w to, że wierzy w 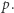 Inaczej mówiąc, jeśli wierzy w
Inaczej mówiąc, jeśli wierzy w 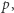 to również wierzy w
to również wierzy w 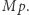
No i w końcu, o normalnym myślaku będziemy mówić, że jest samoświadomy, jeśli wie, że jest normalny. Czyli jeśli dla każdego zdania 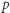 wierzy, że jeśli uwierzy w
wierzy, że jeśli uwierzy w 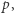 to uwierzy, że uwierzy w
to uwierzy, że uwierzy w 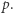 Inaczej mówiąc, wierzy w każde zdanie postaci "jeśli
Inaczej mówiąc, wierzy w każde zdanie postaci "jeśli  to
to 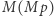 ". O ile myślak normalny nie musi koniecznie wierzyć w to, że jest normalny (ta cecha to właśnie samoświadomość), to okazuje się, że myślaki samoświadome nawet wiedzą, że są samoświadome! Zachęcamy Czytelnika do samodzielnego udowodnienia tego faktu.
". O ile myślak normalny nie musi koniecznie wierzyć w to, że jest normalny (ta cecha to właśnie samoświadomość), to okazuje się, że myślaki samoświadome nawet wiedzą, że są samoświadome! Zachęcamy Czytelnika do samodzielnego udowodnienia tego faktu.
Założymy także, że jeśli ktoś powie do myślaka pewne zdanie  (np. "pada deszcz"), to myślak uwierzy w zupełnie naturalne w tej sytuacji zdanie "ten ktoś mówi prawdę wtedy i tylko wtedy, gdy pada deszcz".
(np. "pada deszcz"), to myślak uwierzy w zupełnie naturalne w tej sytuacji zdanie "ten ktoś mówi prawdę wtedy i tylko wtedy, gdy pada deszcz".
Powiedzmy teraz, że do samoświadomego myślaka przychodzi pewien człowiek. Człowiek ten niech nazywa się Kurt (oczywiście, ku czci Kurta Gödla). Kurt mówi następujące słowa: "nie uwierzysz, że mówię prawdę". Okazuje się, że wtedy myślak, o ile nie jest sprzeczny, nigdy się o tym nie dowie (nigdy w to nie uwierzy, że jest niesprzeczny). Jeśli natomiast myślak jest zuchwały (czyli wierzy, że jest niesprzeczny), to stanie się sprzeczny!
Jak to możliwe? Aby się przekonać, prześledźmy rozumowanie samoświadomego zuchwałego myślaka. A myśli on tak: "Załóżmy, że uwierzę, że Kurt mówi prawdę. To znaczy, że uwierzę w to, co powiedział. Uwierzę, że nie uwierzę, że on mówi prawdę. Ale skoro uwierzę w to, że mówi prawdę, a jestem normalny, to także uwierzę, że wierzę w to, że on mówi prawdę. Zatem jednocześnie uwierzę w to, że nie wierzę, że on mówi prawdę, i w to, że wierzę w to, że mówi prawdę. Czyli uwierzę w dwa przeciwne sobie zdania, czyli stanę się sprzeczny. Ale ja nie mogę się stać sprzeczny". To ostatnie myśli myślak, będąc myślakiem zuchwałym. Rozumuje więc dalej: "Ponieważ to sprzeczność, to założenie, że uwierzę, że Kurt mówi prawdę, nie jest prawdziwe. Wynika z tego, że na pewno nie uwierzę, że Kurt mówi prawdę. A zatem rzeczywiście mówi prawdę". Myślak ten wierzy zatem w to, że Kurt mówi prawdę, a także będąc normalnym, wierzy w to, że wierzy, że Kurt mówi prawdę. Ale myśli dalej: "Wierzę, że on mówi prawdę, a on jednak powiedział, że w to nie uwierzę. Więc nie mówi prawdy". W tym momencie myślak wierzy zarówno w to, że Kurt mówi prawdę, jak i w to, że Kurt nie mówi prawdy. A zatem nasz myślak rzeczywiście popadł w sprzeczność! Do czego może doprowadzić myślaka zuchwałość!
Druga wersja naszego wniosku powinna być zatem jasna. Jeśli myślak jest samoświadomy, ale nie jest sprzeczny, to na pewno nigdy nie uwierzy w to, że nie jest sprzeczny. Gdyby bowiem w to wierzył, wtedy, co pokazaliśmy, jest sprzeczny!
Zauważmy jeszcze, że jeśli zdanie "Kurt mówi prawdę" oznaczymy jako 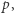 to zdanie, które Kurt wypowiedział, to "nie
to zdanie, które Kurt wypowiedział, to "nie 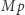 ". W takim razie zdanie, w które w wyniku wypowiedzi Kurta myślak uwierzył, to: "Kurt mówi prawdę wtedy i tylko wtedy, gdy nie
". W takim razie zdanie, w które w wyniku wypowiedzi Kurta myślak uwierzył, to: "Kurt mówi prawdę wtedy i tylko wtedy, gdy nie 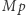 ". Czyli po prostu zdanie "
". Czyli po prostu zdanie " 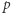 wtedy i tylko wtedy, gdy nie
wtedy i tylko wtedy, gdy nie 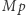 ".
".
Okazuje się, że matematyka jest w pewnym sensie samoświadomym myślakiem, który rozmyśla nad takim właśnie zdaniem. Kurt Gödel udowodnił, że jeśli założymy aksjomatykę, z której wynikają wszystkie twierdzenia arytmetyki liczb naturalnych (tzw. arytmetykę Peano), to system dowodzenia ma właściwości samoświadomego myślaka. W tym wypadku wiara myślaka w pewne zdanie 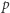 odpowiada możliwości udowodnienia zdania
odpowiada możliwości udowodnienia zdania 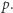 Co więcej, Gödel pokazał, że istnieje zdanie
Co więcej, Gödel pokazał, że istnieje zdanie  takie, że nasz system matematyczny zawiera zdanie postaci "
takie, że nasz system matematyczny zawiera zdanie postaci "  wtedy i tylko wtedy, gdy nie
wtedy i tylko wtedy, gdy nie  " (w tym wypadku
" (w tym wypadku  dla pewnego zdania
dla pewnego zdania 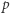 znaczy po prostu, że z przyjętych aksjomatów można udowodnić
znaczy po prostu, że z przyjętych aksjomatów można udowodnić 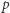 ). Aby znaleźć takie zdanie
). Aby znaleźć takie zdanie 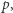 Kurt Gödel wykorzystał sprytny pomysł, który polegał na ponumerowaniu wszystkich możliwych zdań. Czytelnika zainteresowanego, w jaki dokładnie sposób można znaleźć takie zdanie, odsyłamy do podręczników akademickich (np. "Gödel's Theorems", Peter Smith, dostępny w Internecie).
Kurt Gödel wykorzystał sprytny pomysł, który polegał na ponumerowaniu wszystkich możliwych zdań. Czytelnika zainteresowanego, w jaki dokładnie sposób można znaleźć takie zdanie, odsyłamy do podręczników akademickich (np. "Gödel's Theorems", Peter Smith, dostępny w Internecie).
W każdym razie okazuje się, że przyjmując dowolny system aksjomatów zawierający arytmetykę na liczbach naturalnych, jeśli są one niesprzeczne, nie jest możliwe udowodnienie tego faktu. Wobec tego, paradoksalnie, fakt, że nie ma dowodu wewnętrznej niesprzeczności aksjomatów matematyki, można traktować jako pozytywną informację! Inaczej mówiąc, wiadomo, że nie da się udowodnić tego, że aksjomaty matematyki są niesprzeczne (no chyba że są sprzeczne, bo wtedy da się z nich udowodnić wszystko!). Ten fakt nazywany jest drugim twierdzeniem Gödla o niezupełności.
Słowo "niezupełność" w nazwie tego twierdzenia odnosi się do tego, że istnieją takie zdania, których nie da się udowodnić ani obalić, wychodząc od przyjętych aksjomatów. Jako przykład drugie twierdzenie Gödla podaje właśnie zdanie o tym, że aksjomaty są niesprzeczne. Nie jest to jedyny przykład takiego zdania (pierwsze twierdzenie Gödla o niezupełności mówi po prostu, że takie zdanie istnieje). My już poznaliśmy inny przykład takiego zdania - jest nim hipoteza continuum.
Co można z tym począć? Można myśleć na dwa sposoby. Pierwszy z nich to wyobrażenie, że istnieje wiele światów matematycznych. Za każdym razem, gdy spotykamy takie zdanie, jak hipoteza continuum, to będziemy wiedzieli, że istnieją matematyczne światy, w których to zdanie jest prawdziwe, jak też i światy, w których to zdanie jest nieprawdziwe. Możemy myśleć, jakie są konsekwencje dla takiego matematycznego systemu, gdy na przykład hipoteza continuum jest prawdziwa, a jakie, gdy nie jest prawdziwa. Możemy rozważać różne przypadki matematycznych światów.
Można też myśleć, że istnieje jeden prawdziwy matematyczny świat. I po prostu jeszcze nie wiemy, czy hipoteza continuum jest w nim prawdziwa, czy też nie, bowiem nasz system aksjomatów nie jest wystarczająco silny. Trzeba zatem pracować nad znalezieniem nowego aksjomatu - stwierdzenia, które wszyscy uznają za prawdziwe, i to takiego, że dodanie go do aksjomatów rozstrzygnie hipotezę continuum. Oczywiście, zgodnie z twierdzeniem Gödla nadal będą zdania nierozstrzygnięte także przez ten nowy system aksjomatów. Ale to podejście w szczególności oznacza, że chociaż problem hipotezy continuum jest rozwiązany w zakresie przyjętych obecnie aksjomatów, to nie jest rozwiązany w sensie ogólnym.
Sam Gödel był wyznawcą istnienia jednego prawdziwego matematycznego świata. Uważał, że prawdopodobnie hipoteza continuum nie jest prawdziwa - dowód jej nierozstrzygalności uznawał za świadectwo tego, że przyjęte aksjomaty w niewystarczający sposób opisują świat matematyczny. Kwestia ta wywołała sporo dyskusji w matematycznym świecie. Jeden z najwybitniejszych matematyków zajmujących się współcześnie teorią mnogości, Hugh Woodin, zaproponował nowy aksjomat, z którego w szczególności wynika zaprzeczenie hipotezy continuum. Nie można jednak w żaden sposób o tym stwierdzeniu powiedzieć, że oczywiste jest, iż powinno ono być uznane za aksjomat.

wikipedia
Saharon Shelah (1945)
Nie brakuje jednak wybitnych badaczy, których poglądy na matematyczny świat i hipotezę continuum są zbliżone do idei wieloświata matematycznego. Izraelski matematyk, autor niejednego przełomowego odkrycia matematycznego, Saharon Shelah, napisał w artykule "Logical Dreams" z 2003 roku: "Niektórzy uważają, że przekonujące dodatkowe aksjomaty teorii mnogości, które rozstrzygają problemy o dużym znaczeniu, zostaną znalezione lub nawet już zostały znalezione. Trudno dyskutować z tą nadzieją oraz trudno rozważać argumenty, które nie zostały jeszcze zasugerowane. Nie zgadzam się jednak z czystym platońskim poglądem, że interesujące problemy w teorii mnogości można rozstrzygnąć, musimy tylko odkryć dodatkowy aksjomat. Moje wyobrażenie jest takie, że mamy wiele możliwych teorii mnogości, wszystkie zgodne z aksjomatami ZFC" (z podstawowymi aksjomatami teorii mnogości).
Zostawmy ten problem w tym miejscu. Każdy Czytelnik ma prawo do swoich wyobrażeń co do wynikającego z powyższych rozważań obrazu matematyki. Faktem jest, że powszechnie przyjęte aksjomaty nie rozstrzygają, czy istnieją jakieś "nieskończoności" pomiędzy nieskończonością przeliczalną a tą mocy continuum. Możemy jednak z łatwością konstruować nieskończenie wiele (bardzo nieskończenie wiele!) jeszcze większych nieskończoności. Tym zajmiemy się w kolejnym, ostatnim, odcinku naszych przygód z nieskończonością.