Nowości z przeszłości
Stara Delta
Uniwersalny szyfr
W naszych czasach coraz więcej rzeczy staje się tajnych. To dlatego, że nasze życie jest coraz bardziej uzależnione od setek i tysięcy drobiazgów, a kontrolę nad nimi każdy chce zachować dla siebie. Przyjdzie może czas, kiedy na posiadanie tablic logarytmicznych wymagane będzie zezwolenie. Żarty? Mam nadzieję. Na razie grozi nam utajnienie tablic rozkładów liczb na czynniki pierwsze. A oto dlaczego...
Każdy szyfr ma jedną zasadniczą wadę: jeżeli znamy sposób szyfrowania, to i deszyfrowania. Dlatego im więcej osób może przesyłać nam zaszyfrowane wiadomości, tym łatwiej policja rozpracuje naszą siatkę. Nawet, gdy używamy tak doskonałego szyfru, jak ten opisany w przygodach dzielnego wojaka Szwejka (tom III, "Przesławne lanie"). Każdy z nas bez wahania założyłby się, że znajomość sposobu szyfrowania umożliwia odczytanie każdej zaszyfrowanej wiadomości. A tymczasem rzecz ma się trochę inaczej. Oto jak grupa osób może ustalić system szyfrów tak, by
- każda z osób mogła ogłosić publicznie (na przykład w gazecie): adresowane do mnie wiadomości proszę szyfrować tak a tak. Szyfrowaną wiadomość (adresowana do jednej z osób tej grupy) może wysłać dowolna, niekoniecznie wtajemniczona osoba. Dowolna osoba może ogłosić: przystępuję do spółki; proszę przeznaczone dla mnie wiadomości szyfrować tak a tak,
- oraz by zaszyfrowanego komunikatu nie mógł odczytać nikt poza adresatem.
Do zbudowania takiego szyfru posłużono się teorią liczb. Oto nieskomplikowane twierdzenie:
Twierdzenie. Jeżeli liczba naturalna 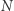 jest iloczynem dwu liczb pierwszych
jest iloczynem dwu liczb pierwszych 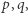 to dla
to dla 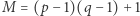 i dla każdego
i dla każdego 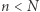 zachodzi
zachodzi
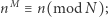 |
tj. 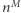 oraz
oraz 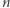 dają z dzielenia przez
dają z dzielenia przez 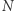 tę samą resztę.
tę samą resztę.
Każda z osób, chcących mieć własny szyfr, wybiera sobie dwie dość duże liczby pierwsze (co najmniej kilkudziesięciocyfrowe) 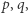 oblicza ich iloczyn
oblicza ich iloczyn 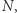 oraz liczbę
oraz liczbę 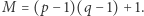 Do wiadomości ogólnej podaje
Do wiadomości ogólnej podaje 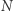 i pewien dzielnik liczby
i pewien dzielnik liczby 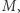 oznaczmy go przez
oznaczmy go przez 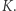 Dla siebie zachowuje rozkład
Dla siebie zachowuje rozkład 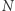 na
na 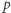 i
i 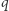 oraz liczbę
oraz liczbę 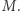 Gdy nadawca NAD chce wysłać wiadomość do odbiorcy ODB, postępuje tak. Zamienia tekst słowny na ciąg cyfr w jakiś standardowy, ustalony i jawny sposób, np.
Gdy nadawca NAD chce wysłać wiadomość do odbiorcy ODB, postępuje tak. Zamienia tekst słowny na ciąg cyfr w jakiś standardowy, ustalony i jawny sposób, np.  itd. Otrzymaną tak dużą liczbę (komunikat nie może być długi) podnosi do potęgi
itd. Otrzymaną tak dużą liczbę (komunikat nie może być długi) podnosi do potęgi 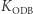 i bierze resztę z dzielenia przez
i bierze resztę z dzielenia przez 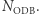 Potrzebna jest do tego maszyna matematyczna, ale nic ponadto. Tak zakodowaną wiadomość (będącą teraz liczbą mniejszą niż
Potrzebna jest do tego maszyna matematyczna, ale nic ponadto. Tak zakodowaną wiadomość (będącą teraz liczbą mniejszą niż 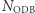 ) wysyła się do odbiorcy lub publikuje w gazecie. Odbiorca winien podnieść tę liczbę do potęgi
) wysyła się do odbiorcy lub publikuje w gazecie. Odbiorca winien podnieść tę liczbę do potęgi 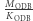 - otrzyma wtedy ciąg liczb wysłany przez nadawcę. Przetworzenie go na tekst słowny odbywa się we wspomniany jawny i standardowy sposób. Co w tym takiego rewelacyjnego? - zapytacie. A to, że podniesienie nawet bardzo dużej liczby do bardzo dużej potęgi
- otrzyma wtedy ciąg liczb wysłany przez nadawcę. Przetworzenie go na tekst słowny odbywa się we wspomniany jawny i standardowy sposób. Co w tym takiego rewelacyjnego? - zapytacie. A to, że podniesienie nawet bardzo dużej liczby do bardzo dużej potęgi 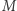 jest dla maszyny matematycznej mało pracochłonne, zwłaszcza że wszystkie obliczenia robi się i tak modulo
jest dla maszyny matematycznej mało pracochłonne, zwłaszcza że wszystkie obliczenia robi się i tak modulo 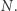 Wynik dostaje się w ułamku sekundy. Osoba postronna nie zna jednak liczby
Wynik dostaje się w ułamku sekundy. Osoba postronna nie zna jednak liczby 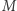 ; mogłaby ją obliczyć, znając
; mogłaby ją obliczyć, znając 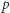 i
i 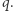 Ale zna tylko
Ale zna tylko 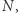 równe
równe 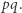 Gdy
Gdy 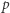 i
i 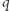 mają po kilkadziesiąt cyfr,
mają po kilkadziesiąt cyfr, 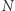 ma sto kilkadziesiąt. Znalezienie rozkładu takiej liczby na czynniki nawet najszybciej działającej maszynie zajęłoby (przy obecnym stanie techniki, informatyki i organizacji maszyn cyfrowych) wiele, wiele lat pracy. Szyfr ten nie daje się złamać najgroźniejszą bronią: analizą statystyczną, rozpracowującą szybko wszystkie szyfry polegające na stałym przyporządkowaniu litera-liczba. Autorzy tego szyfru napisali (w Scientific American), że są niezbicie pewni, iż nikt nie potrafi odczytać zaszyfrowanej przez nich do samych siebie wiadomości.
ma sto kilkadziesiąt. Znalezienie rozkładu takiej liczby na czynniki nawet najszybciej działającej maszynie zajęłoby (przy obecnym stanie techniki, informatyki i organizacji maszyn cyfrowych) wiele, wiele lat pracy. Szyfr ten nie daje się złamać najgroźniejszą bronią: analizą statystyczną, rozpracowującą szybko wszystkie szyfry polegające na stałym przyporządkowaniu litera-liczba. Autorzy tego szyfru napisali (w Scientific American), że są niezbicie pewni, iż nikt nie potrafi odczytać zaszyfrowanej przez nich do samych siebie wiadomości.
Autor Nieznany
***

Komentarz współczesny
Kilka lat temu zapytałem Mordechaja "Motiego" Yunga (obecnie pracuje jako badacz naukowy w Google) o to, na ile zmienił się obraz badań naukowych z dziedziny kryptologii od czasów, gdy zaczynał, a więc od lat 80. W swej odpowiedzi (wyrażonej dość komunikatywną polszczyzną!) jako największą różnicę wskazał liczbę publikowanych prac. Stwierdził, że w początkach swojej kariery był w stanie, bez większego wysiłku, śledzić na bieżąco WSZYSTKIE artykuły dotyczące kryptologii, które ukazywały się na świecie. Dziś natomiast ciężko byłoby młodemu badaczowi przebrnąć w ciągu roku choćby przez połowę publikacji prezentowanych na jednej dużej konferencji kryptologicznej, których organizuje się przecież co najmniej kilka w roku.
Powyższa opinia Motiego dobrze koresponduje z obecnością kryptologii w Delcie. Do końca lat 80. (a więc przez 190 numerów) w Delcie ukazały się tylko dwa krótkie teksty dotyczące zagadnień kryptologicznych - oba prezentujemy w tym numerze. Wówczas była to dziedzina dostarczająca przede wszystkim eleganckich (często zaskakujących) wyników-ciekawostek, kojarzonych głównie ze sztuczkami z teorii liczb. W takim też duchu utrzymane są oba dziś prezentowane wyimki ze 
Oczywiście wraz z rozwojem komputerów i sieci komputerowych znaczenie kryptologii wzrosło niebotycznie. Dziś jest to ogromna gałąź informatyki teoretycznej. Również w Delcie artykułów z tej dziedziny w późniejszym okresie było znacznie więcej. Ostatnio prezentowaliśmy nawet niemal roczny cykl A jednak się da (od Delty 10/2018 do Delty 8/2019), poświęcony w całości kryptologii. Co ciekawe: oba zagadnienia z lat 80. były obecne w tym cyklu (choć autorzy wybierali tematy zupełnie niezależnie), a artykuł otwierający cykl dotyczył dokładnie tego samego tematu, co pierwszy artykuł kryptologiczny w Delcie z roku 1980!
Tomasz Kazana