Nowości z przeszłości
Stara Delta
Czy przez telefon można grać w karty?
O telefonicznej czy korespondencyjnej grze w szachy słyszał każdy. Ale jak grać w ten sposób w brydża lub w pokera? Problemem jest oczywiście rozdawanie kart...
Przypuśćmy, że grają dwie osoby i mają rozdać po pięć kart. Rozdać to znaczy:
- Każdy ma wiedzieć, jakie pięć kart dostał.
- Każdy ma wiedzieć, jakie pięć kart dostał.
- Karty otrzymane przez graczy są różne.
- Żaden z graczy nie ma dodatkowej informacji o kartach partnera, ale po grze może sprawdzić, czy partner nie oszukiwał, czy grał swoimi kartami.
- Każdy rozkład kart jest jednakowo prawdopodobny.
Wszystko to należy wykonać porozumiewając się wyłącznie przez telefon i bez pomocy osób trzecich. Oto sposób umożliwiający w praktyce rozdawanie kart (liczb naturalnych 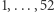 ) przez telefon. Gracze wybierają najpierw dwie rodziny funkcji o argumentach i wartościach naturalnych:
) przez telefon. Gracze wybierają najpierw dwie rodziny funkcji o argumentach i wartościach naturalnych: 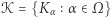 - funkcje kodujące i
- funkcje kodujące i 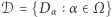 - funkcje dekodujące (zbiór
- funkcje dekodujące (zbiór 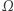 nazywamy zbiorem kodów - powinien on mieć dużo elementów). Rodziny
nazywamy zbiorem kodów - powinien on mieć dużo elementów). Rodziny 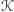 i
i 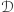 muszą mieć następujące własności:
muszą mieć następujące własności:
- Dziedzina każdej funkcji
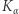 zawiera zbiór
zawiera zbiór 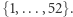
- Dla dowolnego kodu
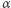 funkcja
funkcja 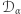 jest odwrotna do funkcji
jest odwrotna do funkcji 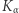 (rozszyfrowuje ona sygnał zakodowany za pomocą funkcji
(rozszyfrowuje ona sygnał zakodowany za pomocą funkcji 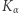 ), tzn.
), tzn. 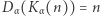 dla liczb naturalnych z dziedziny funkcji
dla liczb naturalnych z dziedziny funkcji 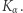
- Dla dowolnych kodów
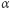 i
i 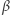 funkcje
funkcje 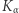 i
i 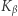 są przemienne, tzn.
są przemienne, tzn. 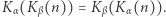
- Różne funkcje kodujące mają rozłączne zbiory wartości.
- Znajomość liczb naturalnych
 i
i 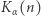 nie daje praktycznie możliwości znalezienia kodu
nie daje praktycznie możliwości znalezienia kodu 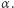
Rozdawanie kart jest już proste. Gracze wybierają (w tajemnicy przed sobą) kody, np. 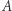 - kod
- kod 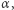
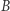 - kod
- kod 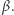 Gracz
Gracz 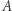 koduje liczby
koduje liczby 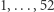 i przesyła je (w dowolnej kolejności) graczowi
i przesyła je (w dowolnej kolejności) graczowi 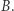 Ten wybiera wpierw pięć kart dla
Ten wybiera wpierw pięć kart dla 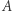 :
: 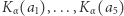 i odsyła mu je -
i odsyła mu je - 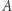 musi je rozszyfrować funkcją
musi je rozszyfrować funkcją 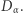 Następnie wybiera pięć kart dla siebie:
Następnie wybiera pięć kart dla siebie: 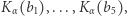 szyfruje je funkcją
szyfruje je funkcją 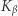 i wysyła do
i wysyła do 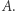 Gracz
Gracz 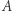 rozszyfrowuje je funkcją
rozszyfrowuje je funkcją 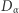 i odsyła do gracza
i odsyła do gracza 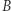 (tzn. przesyła
(tzn. przesyła 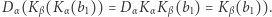 Gracz
Gracz 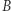 musi jeszcze rozszyfrować je funkcją
musi jeszcze rozszyfrować je funkcją 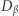 i... karty zostały rozdane.
i... karty zostały rozdane.
Po grze partnerzy ujawniają swoje kody. Z drugiej i czwartej własności rodzin 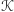 i
i 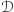 wynika, że jeśli
wynika, że jeśli 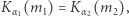 to
to 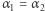 i
i 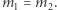 Tak więc gracze nie mogą oszukiwać i podawać innego układu kart i innego kodu.
Tak więc gracze nie mogą oszukiwać i podawać innego układu kart i innego kodu.
Powyższy opis umożliwia w praktyce rozdawanie kart. Teoretycznie bowiem jest to niemożliwe.
***

Komentarz współczesny
Kilka lat temu zapytałem Mordechaja "Motiego" Yunga (obecnie pracuje jako badacz naukowy w Google) o to, na ile zmienił się obraz badań naukowych z dziedziny kryptologii od czasów, gdy zaczynał, a więc od lat 80. W swej odpowiedzi (wyrażonej dość komunikatywną polszczyzną!) jako największą różnicę wskazał liczbę publikowanych prac. Stwierdził, że w początkach swojej kariery był w stanie, bez większego wysiłku, śledzić na bieżąco WSZYSTKIE artykuły dotyczące kryptologii, które ukazywały się na świecie. Dziś natomiast ciężko byłoby młodemu badaczowi przebrnąć w ciągu roku choćby przez połowę publikacji prezentowanych na jednej dużej konferencji kryptologicznej, których organizuje się przecież co najmniej kilka w roku.
Powyższa opinia Motiego dobrze koresponduje z obecnością kryptologii w Delcie. Do końca lat 80. (a więc przez 190 numerów) w Delcie ukazały się tylko dwa krótkie teksty dotyczące zagadnień kryptologicznych - oba prezentujemy w tym numerze. Wówczas była to dziedzina dostarczająca przede wszystkim eleganckich (często zaskakujących) wyników-ciekawostek, kojarzonych głównie ze sztuczkami z teorii liczb. W takim też duchu utrzymane są oba dziś prezentowane wyimki ze 
Oczywiście wraz z rozwojem komputerów i sieci komputerowych znaczenie kryptologii wzrosło niebotycznie. Dziś jest to ogromna gałąź informatyki teoretycznej. Również w Delcie artykułów z tej dziedziny w późniejszym okresie było znacznie więcej. Ostatnio prezentowaliśmy nawet niemal roczny cykl A jednak się da (od Delty 10/2018 do Delty 8/2019), poświęcony w całości kryptologii. Co ciekawe: oba zagadnienia z lat 80. były obecne w tym cyklu (choć autorzy wybierali tematy zupełnie niezależnie), a artykuł otwierający cykl dotyczył dokładnie tego samego tematu, co pierwszy artykuł kryptologiczny w Delcie z roku 1980!
Tomasz Kazana