Praktyczne, bo niepraktyczne, czyli: od teorii liczb do kryptologii

Teoria liczb to prawdopodobnie najstarsza dziedzina wiedzy matematycznej, badana intensywnie już w czasach starożytnych (a zapewne jeszcze wcześniej; możliwe, że nawet zanim powstała jakakolwiek cywilizacja operująca przekazem pisemnym).

Greków niebywale fascynowały liczby pierwsze (umieli udowodnić, że jest ich nieskończenie wiele!) i różne zagadnienia obliczeniowe z nimi związane: potrafili na przykład sprawnie wyznaczać zbiór wszystkich liczb pierwszych nie większych niż 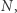$, N$ dla zadanego 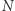$N$ (sito Eratostenesa) czy szybko odnajdować największy wspólny dzielnik (NWD) dwóch liczb naturalnych (algorytm Euklidesa).

W zasadzie przez wszystkie kolejne stulecia zagadnienia z tej dziedziny były zawsze w orbicie zainteresowań matematyków, choć niespecjalnie miało to przełożenie na praktyczne zastosowania. Oczywiście dla rasowego matematyka nigdy nie jest to przeszkodą, a wręcz - co szczególnie podkreślał Carl Gauss - może stanowić, trudną do zrozumienia dla profanów matematyki, dodatkową motywację do ich zgłębiania.

Historia rozwoju teorii liczb jest fascynująca i pełna nieoczekiwanych wyników, jednak ambicją tego tekstu nie jest nawet jej naszkicowanie. Raczej - idąc z duchem numeru Delty, który Czytelnik trzyma w dłoni - chcemy pokazać pewne pojęcia, koncepcje i hipotezy, które znali już Fermat, Gauss, Goldbach czy Euler, a które okazały się użyteczne dopiero po ich śmierci. Innymi słowy, królowa matematyki (że pozwolimy sobie przywołać po raz drugi słowa Gaussa na temat teorii liczb) nie jest aż tak niewinnie i platonicznie piękna, jak naszym wielkim przodkom się wydawało.

Stety czy niestety, w XX wieku matematycy nauczyli się teorię liczb wykorzystywać do bardzo przyziemnych celów.

Algorytmiczna teoria liczb

Jedną z ważnych klas problemów teorii liczb są problemy obliczeniowe. Już w czwartej klasie szkoły podstawowej dzieci uczą się, jak pisemnie dodawać dwie liczby zapisane w systemie dziesiętnym. Łatwo zauważyć, że podany na lekcjach algorytm będzie efektywny (dający się wykonać w rozsądnym czasie na kartce) dla bardzo dużych, nawet kilkudziesięciocyfrowych, liczb.

Nie każdy problem z teorii liczb umiemy efektywnie rozwiązywać. Czasami nawet dla pozornie bardzo podobnych do siebie problemów znamy bardzo różne (w sensie efektywności) jakościowo rozwiązania. Na przykład szukanie NWD dla dwóch nawet bardzo dużych liczb jest szybkie, ale już rozkład na czynniki dużych liczb - obliczeniowo jest w zasadzie poza zasięgiem najszybszych współczesnych komputerów.

Poddziedzina teorii liczb zajmująca się takimi zagadnieniami (co umiemy, a czego nie umiemy efektywnie obliczać dla dużych liczb) nazywana jest algorytmiczną teorią liczb. To właśnie głównie wyniki (zarówno negatywne, jak i pozytywne!) z tego obszaru stały się przyczynkiem do rozwoju kryptologii - jakże praktycznej gałęzi współczesnej informatyki.

Kryptologia

W twierdzeniach kryptologicznych zwykle postulujemy, że przeciwnik (podsłuchiwacz, włamywacz) - nawet jeśli ma częściowy dostęp do systemu (może podsłuchiwać to, co "w eterze", ma ograniczony dostęp do komputera ofiary itp.) - to i tak nie jest w stanie czegoś zrobić - odtworzyć wiadomości, zmienić wartości jakiejś zmiennej itp. Jak w ogóle można podejść do rozwiązania tak postawionego problemu?

Szkic argumentacji jest zwykle podobny: wykazujemy, że gdyby przeciwnik był w stanie coś niecnego zrobić, to korzystając (być może nietrywialnie) ze szczegółów jego ataku, moglibyśmy efektywnie rozwiązać jakiś standardowy problem z algorytmicznej teorii liczb, o którym wiemy (a częściej: w który wierzymy), że jest trudny. Takie wnioskowanie sugeruje, że przesłanka była fałszywa, a więc że jednak taki sprytny przeciwnik po prostu nie istnieje.

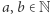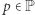I tak: szyfrowanie ElGamala da się zredukować do problemu trudności logarytmu dyskretnego. Problem ten polega na znalezieniu (dla danych $|a,b ∈N$ oraz $|p∈ P$ ) takiej liczby 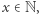$x ∈ N,$ że

ax = b(modp).

Wierzymy, że powyższy problem jest bardzo trudny dla dużych 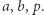$|a,b,p.$ Z drugiej strony, potrafimy ściśle udowodnić, że mając w ręku algorytm 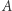$A$ łamiący (w pewnym ściśle określonym sensie) schemat szyfrujący ElGamala, możemy skonstruować algorytm 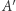$A |$ efektywnie rozwiązujący problem logarytmu dyskretnego.

Z powyższych dwóch faktów (a raczej: jednego postulatu "na wiarę" i jednego ścisłego rozumowania) wprost wynika, że nie może istnieć żaden algorytm łamiący szyfr ElGamala.

W podobnym duchu wykorzystuje się przeróżne założenia z algorytmicznej teorii liczb do dowodzenia bezpieczeństwa różnych, często bardzo nietrywialnych, protokołów kryptologicznych. Oczywiście staramy się, aby założeń teorioliczbowych było jak najmniej oraz aby były one jak najbardziej standardowe. Poza wyżej wyeksponowanym problemem logarytmu dyskretnego często wykorzystywanymi w kryptologii założeniami są m.in.:

trudność rozkładu dużych liczb na czynniki pierwsze;
trudność logarytmu dyskretnego w grupie punktów krzywej eliptycznej (zob. Delta 08/2018);
trudność stwierdzania, czy dana liczba 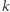$k |$ jest resztą kwadratową modulo 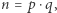$|n = p ⋅q,$ dla pewnych danych 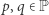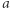$p, q∈ P$ ( $a$ jest resztą kwadratową modulo 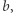$b,$ gdy istnieje 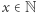$x ∈ N$ taki, że 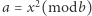$a = x2(modb)$ ). Ten problem jest problemem decyzyjnym ( 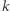$k$ albo jest, albo nie jest resztą kwadratową modulo 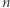$|n$ ), więc trudność oznacza tu, że nie umiemy znaleźć algorytmu, który osiąga prawdopodobieństwo sukcesu istotnie większe niż $50%$ ;
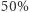pewna ustalona funkcja 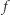$f$ (np. funkcja SHA-3) ma własność funkcji jednokierunkowej, a więc dla danego losowego 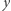$y$ bardzo trudne jest znalezienie dowolnego 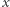$x$ takiego, że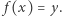 $f(x) = y.$

Powyższe założenia nie wyczerpują pełnego zakresu popularnych założeń teorioliczbowych, ale stanowią już potężną bazę, z której da się zbudować niezwykle wyrafinowane konstrukcje kryptologiczne, takie jak podpis cyfrowy, obliczenia wielopodmiotowe, dowody z wiedzą zerową, szyfrowanie asymetryczne, elektroniczna gotówka i inne.

Protokoły kryptologiczne są często bardzo pomysłowe, a dowody ich redukcji należą do trudnych zagadnień z algorytmicznej teorii liczb - niejednokrotnie są trikowe i nieoczywiste. Z braku miejsca w tym tekście nie umieszczamy konkretnych przykładów, pozostając w obszarze dywagacji ogólnych. Chętnych do dokładniejszego zgłębienia tych zagadnień zapraszam do prześledzenia cyklu A jednak się da, który proponowaliśmy w Delcie od numeru Delta 10/2018 do numeru Delta 08/2019. Dodatkowo - można to zrobić, wyczulając się szczególnie na precyzyjną analizę, jakie konkretnie założenia teorioliczbowe stoją za rozpatrywanymi protokołami. To może być bardzo pouczające ćwiczenie!

Myślę, że naprawdę warto, tym bardziej że jest to przecież ta część osiągnięć ludzkości, która nawet nie śniła się takim tuzom matematyki, jak sam książę Carl Gauss.