A jednak się da!
Nie wiem, ale powiem (AJSD VII)
Wyobraźmy sobie następującą wakacyjną historię miłosną, która miała prawo się zdarzyć przed nastaniem ery wszechobecnych mediów społecznościowych...
To, czego potrzeba Bogumiłowi do szczęścia, to protokół prywatnego uzyskiwania informacji (jest to próba tłumaczenia angielskiego terminu private information retrieval), czyli sposób na odpytywanie bazy danych (Dobromira) tak, aby baza danych nie wiedziała, o co ją pytamy, i mimo to dostarczyła odpowiedzi (tytułowe nie wiem, ale powiem). Oczywiście Bogumił mógłby poprosić o przesłanie całej bazy danych (czyli o przedyktowanie zawartości całego zeszytu), ale zależy mu na tym, by zminimalizować ilość przesyłanej informacji. Zaprawieni w lekturze kącika AJSD Czytelnicy nie powinni mieć trudności z przetłumaczeniem tego problemu na bardziej matematyczny język: Dobromir zna ciąg bitów 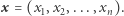 Bogumił chce poznać wartość
Bogumił chce poznać wartość 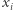 dla wybranego przez siebie
dla wybranego przez siebie 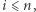 jednak nie chce zdradzić Dobromirowi wartości
jednak nie chce zdradzić Dobromirowi wartości 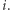 Zakładamy, że każda informacja wysłana do i od Dobromira kosztuje, a Bogumił chce uczynić ten koszt jak najmniejszym. Wydaje się, że nie może on zrobić niczego istotnie lepszego od poproszenia Dobromira o cały ciąg
Zakładamy, że każda informacja wysłana do i od Dobromira kosztuje, a Bogumił chce uczynić ten koszt jak najmniejszym. Wydaje się, że nie może on zrobić niczego istotnie lepszego od poproszenia Dobromira o cały ciąg  Cóż, a jednak się da!
Cóż, a jednak się da!
Kolegów dwóch (lub więcej)
Na początku uprośćmy sytuację i załóżmy, że Bogumił ma jeszcze jednego kolegę, Eustachego, który zna 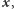 ponadto nie zna się on z Dobromirem. Wówczas Bogumił mógłby zastosować następującą egzotyczną (i, jak się zaraz okaże, niezbyt mądrą) procedurę: losuje ciąg binarny
ponadto nie zna się on z Dobromirem. Wówczas Bogumił mógłby zastosować następującą egzotyczną (i, jak się zaraz okaże, niezbyt mądrą) procedurę: losuje ciąg binarny 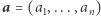 i prosi Dobromira o przesłanie
i prosi Dobromira o przesłanie 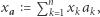 a Eustachego o
a Eustachego o 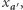 gdzie
gdzie 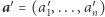 to ciąg
to ciąg 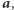 w którym wartość
w którym wartość 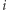 -tego bitu została zmieniona (tzn.
-tego bitu została zmieniona (tzn. 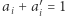 oraz
oraz 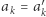 dla
dla 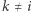 ). Okazuje się, że wówczas
). Okazuje się, że wówczas 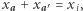 gdyż
gdyż
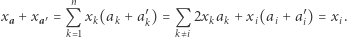 |
W tej sytuacji, znając 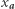 oraz
oraz 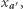 Bogumił jest w stanie odtworzyć
Bogumił jest w stanie odtworzyć 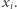 Z drugiej strony, ciąg
Z drugiej strony, ciąg 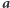 jest losowy, więc nie dostarcza Dobromirowi żadnej informacji o
jest losowy, więc nie dostarcza Dobromirowi żadnej informacji o 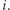 Ponadto z punktu widzenia Eustachego ciąg
Ponadto z punktu widzenia Eustachego ciąg 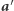 jest losowy (co wymaga być może krótkiej chwili zastanowienia), więc on też nie uzyskuje żadnej informacji o
jest losowy (co wymaga być może krótkiej chwili zastanowienia), więc on też nie uzyskuje żadnej informacji o 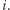 Zauważmy, że gdyby Dobromir i Eustachy połączyli siły, to mogliby łatwo odtworzyć
Zauważmy, że gdyby Dobromir i Eustachy połączyli siły, to mogliby łatwo odtworzyć 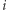 - jest to jedyny indeks, na którym różnią się ciągi
- jest to jedyny indeks, na którym różnią się ciągi 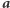 i
i 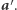 Zakładamy jednak, że nie komunikują się oni ze sobą, zatem Bogumił nie musi się przejmować taką ewentualnością.
Zakładamy jednak, że nie komunikują się oni ze sobą, zatem Bogumił nie musi się przejmować taką ewentualnością.
Jak już wspomnieliśmy, powyższy sposób - choć wykorzystuje pewne chytre obserwacje - jest dla Bogumiła bezwartościowy. Przypomnijmy bowiem, że przesył informacji w obie strony jest kosztowny, a w zaprezentowanym protokole Bogumił wysyła dwa ciągi długości 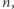 czyli aż
czyli aż 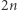 bitów. Już (dwa razy) lepiej byłoby poprosić Dobromira o przesłanie całego ciągu
bitów. Już (dwa razy) lepiej byłoby poprosić Dobromira o przesłanie całego ciągu 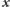 !
!
Rzecz jasna, nie zaprezentowaliśmy powyższej idei tylko po to, by stwierdzić jej bezużyteczność. Okazuje się, że można ją tak zmodyfikować, żeby jednak coś na niej zyskać. W tym celu potrzebujemy kolejnych dwóch kolegów z dostępem do 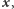 którzy się ze sobą nie komunikują. Umieśćmy wartości
którzy się ze sobą nie komunikują. Umieśćmy wartości 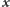 w kwadratowej tablicy
w kwadratowej tablicy ![-- X= [xk,l]k,lDm](/math/temat/matematyka/kryptologia/2019/05/24/Nie_wiem_ale_powiem/3x-cecb4f44e6e38c3b76b1007e8e96d5c44d374433-im-33,33,33-FF,FF,FF.gif) rozmiaru
rozmiaru 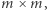 gdzie
gdzie 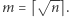 Powiedzmy, że
Powiedzmy, że 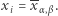 Tym razem Bogumił losuje dwa binarne ciągi
Tym razem Bogumił losuje dwa binarne ciągi 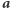 i
i 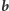 długości
długości 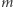 i wysyła je Dobromirowi. Dobromir oblicza
i wysyła je Dobromirowi. Dobromir oblicza 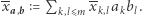 Podobnie jak poprzednio niech
Podobnie jak poprzednio niech 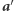 powstaje z
powstaje z 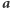 przez zmianę
przez zmianę 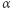 -tego bitu, a
-tego bitu, a 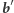 powstaje z
powstaje z 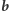 przez zmianę
przez zmianę 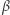 -tego bitu. Do kolejnych znajomych Bogumił wysyła pary ciągów bitów
-tego bitu. Do kolejnych znajomych Bogumił wysyła pary ciągów bitów 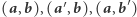 i
i 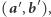 otrzymując od nich
otrzymując od nich 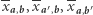 oraz
oraz 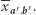 Wówczas w sumie
Wówczas w sumie 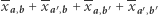
- dla
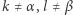 składnik
składnik 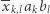 liczony jest cztery razy (występuje w każdej składowej sumie), więc nie jest liczony wcale,
liczony jest cztery razy (występuje w każdej składowej sumie), więc nie jest liczony wcale, - dla
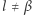 składnik
składnik 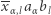 liczony jest dwa razy, tak samo jak
liczony jest dwa razy, tak samo jak 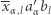 ; obu nie musimy zatem liczyć,
; obu nie musimy zatem liczyć, - dla
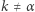 składniki
składniki 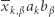 i
i 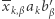 liczone są dwa razy, więc podobnie jak w poprzednim punkcie nie wpływają na wynik,
liczone są dwa razy, więc podobnie jak w poprzednim punkcie nie wpływają na wynik, - wśród liczb
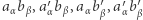 są trzy zera i jedynka, a zatem suma składników
są trzy zera i jedynka, a zatem suma składników 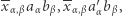
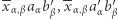 daje
daje 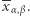

Powyższe rozważania dowodzą, że 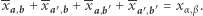 Bogumił uzyskuje zatem szukaną wartość
Bogumił uzyskuje zatem szukaną wartość 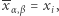 a jego koledzy nie dowiadują się niczego o
a jego koledzy nie dowiadują się niczego o 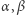 (co uzasadniamy tak jak poprzednio). Tym razem wykorzystujemy cztery bazy danych, ale za to rozmiar naszej komunikacji to
(co uzasadniamy tak jak poprzednio). Tym razem wykorzystujemy cztery bazy danych, ale za to rozmiar naszej komunikacji to 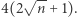 W analogiczny sposób, poprzez zapisanie
W analogiczny sposób, poprzez zapisanie  w
w 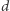 -wymiarowej tablicy i wykorzystanie
-wymiarowej tablicy i wykorzystanie 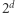 baz danych, możemy dokonać prywatnego uzyskania informacji przy komunikacji rozmiaru
baz danych, możemy dokonać prywatnego uzyskania informacji przy komunikacji rozmiaru 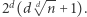 Widzimy zatem, że możemy w ten sposób uzyskać dowolnie mały wykładnik przy
Widzimy zatem, że możemy w ten sposób uzyskać dowolnie mały wykładnik przy 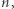 jednak kosztem wykładniczo rosnącej liczby potrzebnych, nieskomunikowanych baz danych.
jednak kosztem wykładniczo rosnącej liczby potrzebnych, nieskomunikowanych baz danych.
...a może jednak wystarczy jeden?
Co, jeśli nie jesteśmy w tak wygodnej sytuacji i Bogumił jest skazany wyłącznie na Dobromira? Czy możemy istotnie zmniejszyć koszt transmisji, mając do czynienia tylko z jedną bazą danych? Cóż, gdyby było inaczej, temat niekoniecznie zasługiwałby na prezentację w naszym kąciku. Okazuje się, że nawet mając do dyspozycji jeden egzemplarz bazy danych, możemy dokonać "prywatnego zapytania" kosztem rzędu rozmiaru bazy danych podniesionego do dowolnie małej potęgi. Po raz pierwszy taki magiczny sposób zaproponowali Eyal Kuszilewić i Rafail Ostrowski w 1997 roku. Aby dokonać jego prezentacji, musimy przedstawić małe przypomnienie z teorii liczb (patrz również artykuł o commicie w Delcie 11/2018).
Wykorzystując przedstawioną teorię, możemy zaproponować następujący protokół prywatnego uzyskiwania informacji dla jednej bazy danych (Dobromira):
- (a)
- Bogumił i Dobromir umawiają się na reprezentację ciągu
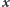 w postaci tablicy
w postaci tablicy ![|X= [xk,l]kDs,lDt.](/math/temat/matematyka/kryptologia/2019/05/24/Nie_wiem_ale_powiem/2x-e7020da0d8b0cbbc9e3b27ffbc192b2c02759848-im-33,33,33-FF,FF,FF.gif) Załóżmy, że
Załóżmy, że 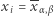 ;
; - (b)
- Bogumił wybiera duże liczby pierwsze
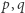 (których reprezentacja dwójkowa ma
(których reprezentacja dwójkowa ma 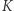 bitów) i oblicza
bitów) i oblicza 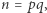 po czym wybiera losowo
po czym wybiera losowo 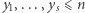 w taki sposób, że
w taki sposób, że 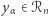 oraz
oraz 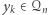 dla
dla 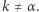 Następnie przekazuje
Następnie przekazuje  oraz wszystkie liczby
oraz wszystkie liczby 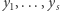 Dobromirowi. Zauważmy, że zgodnie z naszą uwagą Dobromir (nieznający
Dobromirowi. Zauważmy, że zgodnie z naszą uwagą Dobromir (nieznający 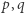 ) dla żadnego
) dla żadnego 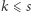 nie jest w stanie stwierdzić, czy
nie jest w stanie stwierdzić, czy 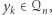 nie dowie się zatem niczego o
nie dowie się zatem niczego o 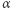 ;
; - (c)
- Dla każdego
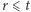 Dobromir oblicza
Dobromir oblicza 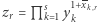 modulo
modulo 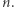 Jest to iloczyn wszystkich wysłanych liczb
Jest to iloczyn wszystkich wysłanych liczb 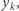 przy czym niektóre - te, którym w
przy czym niektóre - te, którym w  -tej kolumnie odpowiada jedynka - mnożone są "w kwadracie". Ponieważ tylko
-tej kolumnie odpowiada jedynka - mnożone są "w kwadracie". Ponieważ tylko 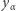 nie jest kwadratem modulo
nie jest kwadratem modulo 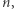 więc
więc 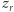 jest kwadratem tylko wtedy, gdy
jest kwadratem tylko wtedy, gdy 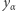 jest mnożone "w kwadracie", czyli gdy
jest mnożone "w kwadracie", czyli gdy 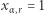 ;
; - (d)
- Bogumił sprawdza, czy
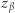 jest kwadratem (może to uczynić, gdyż zna
jest kwadratem (może to uczynić, gdyż zna 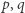 ). Jeśli tak, to
). Jeśli tak, to 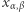 wynosi 1, w przeciwnym przypadku 0.
wynosi 1, w przeciwnym przypadku 0.
Przedstawiona komunikacja zajmuje 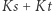 bitów, czyli w ten sposób, biorąc
bitów, czyli w ten sposób, biorąc 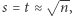 możemy już osiągnąć komunikację rozmiaru
możemy już osiągnąć komunikację rozmiaru 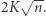 A można jeszcze lepiej! Zauważmy, że spośród skonstruowanych przez Dobromira liczb
A można jeszcze lepiej! Zauważmy, że spośród skonstruowanych przez Dobromira liczb 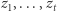 Bogumiła interesuje tylko
Bogumiła interesuje tylko 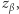 przy czym nie chce on, by Dobromir poznał
przy czym nie chce on, by Dobromir poznał 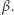 Toż to brzmi dokładnie jak wyjściowy problem, więc rzecz pachnie rekurencją na kilometr! Bogumił może zastosować ten sam protokół dla ciągu
Toż to brzmi dokładnie jak wyjściowy problem, więc rzecz pachnie rekurencją na kilometr! Bogumił może zastosować ten sam protokół dla ciągu 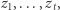 aby poznać
aby poznać 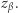 Wówczas rozmiar komunikacji jest rzędu
Wówczas rozmiar komunikacji jest rzędu 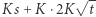 ; optymalizując ze względu na
; optymalizując ze względu na 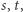 pod warunkiem
pod warunkiem 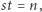 dostajemy koszt
dostajemy koszt 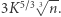 W ten rekurencyjny sposób możemy dowolnie zbijać wykładnik przy
W ten rekurencyjny sposób możemy dowolnie zbijać wykładnik przy  (odwrotnie proporcjonalnie do głębokości rekurencji); niestety, kosztem puchnącego (z grubsza liniowo wraz z głębokością rekurencji) wykładnika przy
(odwrotnie proporcjonalnie do głębokości rekurencji); niestety, kosztem puchnącego (z grubsza liniowo wraz z głębokością rekurencji) wykładnika przy 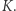 Cóż, odwołując się do klasyka, nie udało nam się przyrządzić zupełnie darmowego obiadu, mamy jednak nadzieję, że Czytelnicy i tak docenią (podobnie jak Bogumił) chytrość i elegancję przedstawionych protokołów.
Cóż, odwołując się do klasyka, nie udało nam się przyrządzić zupełnie darmowego obiadu, mamy jednak nadzieję, że Czytelnicy i tak docenią (podobnie jak Bogumił) chytrość i elegancję przedstawionych protokołów.
 będzie liczbą naturalną. Kwadratem z dzielenia przez
będzie liczbą naturalną. Kwadratem z dzielenia przez 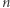 nazwiemy taką liczbę naturalną
nazwiemy taką liczbę naturalną 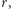 że istnieje
że istnieje 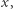 dla którego
dla którego 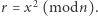 Dla przykładu, 23 jest kwadratem z dzielenia przez 7, gdyż
Dla przykładu, 23 jest kwadratem z dzielenia przez 7, gdyż 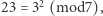 ale 3 już nim nie jest. Oznaczmy przez
ale 3 już nim nie jest. Oznaczmy przez 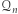 zbiór kwadratów z dzielenia przez
zbiór kwadratów z dzielenia przez 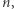 które są względnie pierwsze z
które są względnie pierwsze z 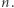 Dla
Dla 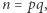 gdzie
gdzie 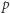 i
i 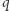 są różnymi liczbami pierwszymi, można nietrudno pokazać, że
są różnymi liczbami pierwszymi, można nietrudno pokazać, że 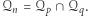 Niech
Niech 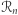 będzie zbiorem liczb względnie pierwszych z
będzie zbiorem liczb względnie pierwszych z 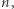 które nie należą ani do
które nie należą ani do 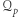 ani do
ani do 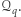 Można pokazać, że
Można pokazać, że 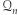 i
i 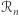 "zachowują się" jak liczby dodatnie i ujemne, to znaczy: pomnożenie dwóch liczb z
"zachowują się" jak liczby dodatnie i ujemne, to znaczy: pomnożenie dwóch liczb z 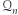 lub dwóch liczb
lub dwóch liczb 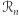 daje liczbę z
daje liczbę z 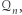 a pomnożenie liczby z
a pomnożenie liczby z 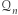 i liczby z
i liczby z 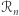 daje liczbę z
daje liczbę z 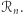 Ponadto, dla dużych wartości
Ponadto, dla dużych wartości 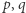 stwierdzenie, czy liczba z
stwierdzenie, czy liczba z 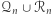 należy do
należy do 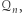 jest trudne obliczeniowo, jeśli znamy tylko wartość
jest trudne obliczeniowo, jeśli znamy tylko wartość  (a bardzo łatwe, jeśli znamy
(a bardzo łatwe, jeśli znamy 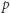 i
i 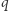 ).
).