A jednak się da!
O cyfrowej gotówce (ASJD VI)
Za co kochamy gotówkę? Chyba przede wszystkim za anonimowość transakcji. To znaczy: jeśli Aldona oraz Celina podejmą z banku po banknocie stuzłotowym; następnie Aldona wyda te pieniądze w sklepiku Bogumiła, a Celina u Dobromira; po czym zarówno Bogumił, jak i Dobromir zdeponują zarobione pieniądze z powrotem w banku, to oczywiście bank w żaden sposób nie będzie w stanie stwierdzić, czy klientką Bogumiła była Aldona, czy też może Celina.
Czy podobną właściwość mogą mieć pieniądze cyfrowe, to znaczy takie, gdzie rolę banknotów przejmą zwyczajne pliki komputerowe?
Pierwsza, bardzo naiwna próba skonstruowania takiego systemu mogłaby wyglądać tak, że bank wypłacający Aldonie pieniądze przekazuje jej po prostu plik banknot_v1.txt o treści "100 złotych". Oczywiście takie podejście nie jest mądre, bo przecież taki plik może każdy łatwo sam stworzyć, więc w takim systemie każdy mógłby sam sobie drukować dowolną ilość pieniędzy.

Spróbujmy sytuację poprawić, dodając podpis banku do treści pliku. To znaczy myślimy teraz o pliku:
banknot_v2.txt:
"100 złotych, podpis cyfrowy banku: ad47gh23hg5ewgh3"
Takie podejście nie poprawia niestety znacząco sytuacji. Co prawda nikt sam z siebie łatwo takiego banknotu nie wygeneruje, ale każdy, kto posiada już choćby jeden taki banknot, może go wielokrotnie skopiować i wydawać wiele razy!
To może rozważmy wersję trzecią:
banknot_v3.txt:
"100 złotych wydane Aldonie (ID = 3287392) dnia
5 kwietnia 2019, podpis cyfrowy banku: 38fsu4fhsjk4b4"
Przy takim formacie cyfrowych banknotów oczywiście jakiekolwiek fałszerstwo będzie szybko wykryte, ale - niestety - tracimy nasz główny cel, mianowicie anonimowość transakcji...
Wydaje się, że stoimy pod ścianą. To znaczy, fundamentalne logiczne prawo wyłączonego środka (tertium non datur) powiada, że: albo
(a) w treści pliku banknotu jest zawarta informacja o osobie pobierającej go z banku;
albo
(b) w treści pliku banknotu nie ma tej informacji.
I teraz: w przypadku formatu typu (a) tracimy anonimowość, a w przypadku (b) - jesteśmy zawsze narażeni na niewyrafinowany atak jak wyżej. To znaczy, właściciel banknotu, który nie zawiera informacji o nim, nieważne jak wymyślny byłby format jego zapisu, zawsze może po prostu go skopiować i wydać dwa razy...
A jednak! Zaprezentujemy za chwilę system cyfrowych banknotów, którego nie będzie cechował żaden z dwu powyższych mankamentów. Wysokopoziomowa intuicja stojąca za jego ideą jest taka, że - co prawda w banknocie jest zawarta informacja o jego pierwotnym właścicielu - zapisana jednak w taki sposób, że jednokrotnie wydany banknot będzie wymagał nieosiągalnej mocy obliczeniowej, aby wyciągnąć z niego informację o właścicielu, ale już dwie kopie wydanego (w nieuprawniony sposób) dwa razy banknotu - łatwo to umożliwią. (Nieco oczywiście upraszczamy. W istocie nie będą to dwie identyczne kopie. Protokół płacenia wymusi pewne wzbogacenie banknotu o - za każdym razem nieco inne - dodatkowe informacje.)
Opis systemu cyfrowej gotówki
Tym razem treść pliku banknotu będzie składała się z ciągu liczb 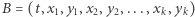 oraz podpisu cyfrowego banku
oraz podpisu cyfrowego banku 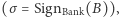 który uwierzytelnia ten ciąg. (Dla uproszczenia, w treści pomijamy nominał banknotu. Możemy przecież umówić się, że wszystkie cyfrowe banknoty są równoważne i mają np. wartość 1 zł.) Załóżmy, że taki właśnie banknot podjęła z banku Aldona, utożsamiana z identyfikatorem
który uwierzytelnia ten ciąg. (Dla uproszczenia, w treści pomijamy nominał banknotu. Możemy przecież umówić się, że wszystkie cyfrowe banknoty są równoważne i mają np. wartość 1 zł.) Załóżmy, że taki właśnie banknot podjęła z banku Aldona, utożsamiana z identyfikatorem 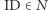 (liczbą rzędu kilkuset cyfr).
(liczbą rzędu kilkuset cyfr).
Liczba 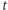 jest tu zupełnie losowa i odgrywa rolę wyłącznie identyfikatora banknotu, natomiast liczby
jest tu zupełnie losowa i odgrywa rolę wyłącznie identyfikatora banknotu, natomiast liczby 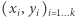 nie są byle jakie, ale spełniają następujące specyficzne warunki:
nie są byle jakie, ale spełniają następujące specyficzne warunki:

Przypomnijmy, że 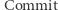 oznacza zobowiązanie, o którym pisaliśmy w drugim odcinku sagi.
oznacza zobowiązanie, o którym pisaliśmy w drugim odcinku sagi.
(Telegraficzny skrót wiedzy o zobowiązaniach: po opublikowaniu 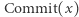 praktycznie nie jest możliwe odczytanie
praktycznie nie jest możliwe odczytanie 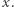 Otworzyć zobowiązanie (ujawniając
Otworzyć zobowiązanie (ujawniając 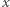 ) może tylko jego autor, przy czym - nie jest w stanie oszukać, czyli wmówić, że w zobowiązaniu znajdował się jakiś
) może tylko jego autor, przy czym - nie jest w stanie oszukać, czyli wmówić, że w zobowiązaniu znajdował się jakiś 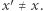 )
)
Teraz opiszemy, jak wygląda wydanie takiego banknotu, na przykładzie płatności dokonanej przez Aldonę w sklepiku Bogumiła:
- 1.
- Aldona, po spakowaniu i sprawdzeniu zakupów, wyraża gotowość przekazania swojego banknotu Bogumiłowi;
- 2.
- Ucieszony Bogumił losuje ciąg
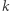 bitów
bitów 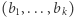 i oznajmia je Aldonie;
i oznajmia je Aldonie; - 3.
- Aldona przekazuje Bogumiłowi plik banknotu (czyli wszystkie liczby
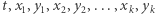 oraz podpis
oraz podpis 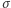 ) i dodatkowo otwiera część zobowiązań zawartych w banknocie. Konkretnie: (dla każdego
) i dodatkowo otwiera część zobowiązań zawartych w banknocie. Konkretnie: (dla każdego 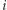 ) jeśli
) jeśli 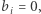 to otwiera
to otwiera 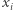 (wówczas Bogumił poznaje
(wówczas Bogumił poznaje 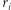 ), a jeśli
), a jeśli 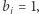 to otwiera
to otwiera 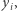 ujawniając wartość
ujawniając wartość 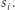
- 4.
- Bogumił sprawdza, czy podpis banku
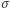 jest poprawny oraz czy protokół otwarcia przebiegł prawidłowo. Jeśli tak - to może pożegnać Aldonę i zachować w pamięci komputera jej banknot wraz z dodatkowymi wartościami z otwartych zobowiązań.
jest poprawny oraz czy protokół otwarcia przebiegł prawidłowo. Jeśli tak - to może pożegnać Aldonę i zachować w pamięci komputera jej banknot wraz z dodatkowymi wartościami z otwartych zobowiązań.

A co się stanie, gdy Bogumił zdeponuje ten banknot w banku? Najpierw bank sprawdzi dokładnie to samo, co Bogumił w ostatnim kroku, czyli autentyczność własnego podpisu oraz poprawność otwartych zobowiązań. Jeśli ten test się powiedzie, to bank weryfikuje jeszcze jedną rzecz: upewnia się, że do tej pory nikt jeszcze nie przyszedł z banknotem o identyfikatorze 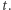 Jeśli nie, to zwiększa saldo konta Bogumiła oraz archiwizuje wartość
Jeśli nie, to zwiększa saldo konta Bogumiła oraz archiwizuje wartość 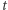 wraz z całym otrzymanym banknotem. Problem pojawia się, gdy banknot o numerze
wraz z całym otrzymanym banknotem. Problem pojawia się, gdy banknot o numerze 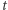 już ktoś wcześniej przyniósł, chociażby Dobromir. Oznacza to, że ktoś, niestety, oszukał i wydał swój banknot dwukrotnie. (Zakładamy, że szansa, iż dwa różne banknoty będą miały ten sam losowy identyfikator, jest zaniedbywalna.) Kto? Prawie na pewno uda nam się to zaraz stwierdzić! Wystarczy do tego dodatkowa wiedza, o którą proszony jest płatnik podczas każdej transakcji. Zauważmy, że bank dysponuje teraz dwoma niezależnymi zestawami takiej wiedzy. Jeśli
już ktoś wcześniej przyniósł, chociażby Dobromir. Oznacza to, że ktoś, niestety, oszukał i wydał swój banknot dwukrotnie. (Zakładamy, że szansa, iż dwa różne banknoty będą miały ten sam losowy identyfikator, jest zaniedbywalna.) Kto? Prawie na pewno uda nam się to zaraz stwierdzić! Wystarczy do tego dodatkowa wiedza, o którą proszony jest płatnik podczas każdej transakcji. Zauważmy, że bank dysponuje teraz dwoma niezależnymi zestawami takiej wiedzy. Jeśli 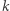 jest dostatecznie duże, to niemal na pewno (dla choć jednego
jest dostatecznie duże, to niemal na pewno (dla choć jednego 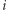 ) w jednym zestawie ujawniono
) w jednym zestawie ujawniono 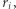 a w drugim:
a w drugim: 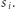 Ale przecież dodanie tych dwóch wartości ujawnia wprost identyfikator oszusta!
Ale przecież dodanie tych dwóch wartości ujawnia wprost identyfikator oszusta!
Jak widać powyżej, problem oszukiwania jest rozwiązany. A co z anonimowością? Oczywiście jest w miarę jasne, że sam ciąg 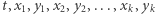 oraz tylko jeden zestaw wiedzy dodatkowej nie zdradzają identyfikatora pierwotnego właściciela banknotu. To prawda, ale haczyk jest gdzie indziej. Nigdzie do tej pory nie opisaliśmy, jak wygląda protokół podjęcia banknotu przez Aldonę. Gdyby miało to wyglądać po prostu tak, że bank sprawdza i podpisuje ciąg
oraz tylko jeden zestaw wiedzy dodatkowej nie zdradzają identyfikatora pierwotnego właściciela banknotu. To prawda, ale haczyk jest gdzie indziej. Nigdzie do tej pory nie opisaliśmy, jak wygląda protokół podjęcia banknotu przez Aldonę. Gdyby miało to wyglądać po prostu tak, że bank sprawdza i podpisuje ciąg 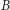 wybrany przez Aldonę, to przecież nikt mu nie zabroni zapamiętać sobie tego
wybrany przez Aldonę, to przecież nikt mu nie zabroni zapamiętać sobie tego 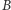 na przyszłość. Wówczas, już po wizycie Bogumiła, nie musi więc starać się otwierać zobowiązań zawartych w
na przyszłość. Wówczas, już po wizycie Bogumiła, nie musi więc starać się otwierać zobowiązań zawartych w 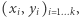 tylko najzwyczajniej może sprawdzić, komu kiedyś przekazał
tylko najzwyczajniej może sprawdzić, komu kiedyś przekazał 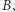 aby zidentyfikować Aldonę... Aby nasz system naprawić, musi nastąpić przedziwna sytuacja, w której Aldona jakoś otrzyma od banku poprawną parę
aby zidentyfikować Aldonę... Aby nasz system naprawić, musi nastąpić przedziwna sytuacja, w której Aldona jakoś otrzyma od banku poprawną parę 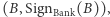 a z drugiej strony - bank nic nie będzie wiedział o
a z drugiej strony - bank nic nie będzie wiedział o 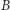 ! Ten punkt brzmi jak magia, ale Czytelnik Pamiętający Część Pierwszą Tej Sagi
! Ten punkt brzmi jak magia, ale Czytelnik Pamiętający Część Pierwszą Tej Sagi 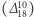 zna już podobne dziwy, a konkretnie: ślepy podpis. Niestety, okazuje się, że w naszym przypadku i ślepy podpis to nie jest dokładnie to, o co nam chodzi. Dlaczego? Otóż bank nie chce, bynajmniej, podpisać byle czego. Sytuacja jest nieco subtelniejsza. Bank chciałby podpisać pewien ciąg
zna już podobne dziwy, a konkretnie: ślepy podpis. Niestety, okazuje się, że w naszym przypadku i ślepy podpis to nie jest dokładnie to, o co nam chodzi. Dlaczego? Otóż bank nie chce, bynajmniej, podpisać byle czego. Sytuacja jest nieco subtelniejsza. Bank chciałby podpisać pewien ciąg 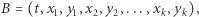 ale w taki sposób, że - godząc się, iż wprost niczego o wartościach elementów
ale w taki sposób, że - godząc się, iż wprost niczego o wartościach elementów 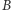 się nie dowie - ma przynajmniej gwarancję, że zachodzi warunek
się nie dowie - ma przynajmniej gwarancję, że zachodzi warunek 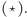 Gdyby tak nie było, to sytuacja naszego systemu byłaby rozpaczliwie dramatyczna - nieuczciwa Aldona mogłaby przecież zażądać od banku ślepego podpisu na ciągu
Gdyby tak nie było, to sytuacja naszego systemu byłaby rozpaczliwie dramatyczna - nieuczciwa Aldona mogłaby przecież zażądać od banku ślepego podpisu na ciągu 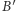 takim, że odpowiednie
takim, że odpowiednie 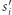 oraz
oraz 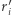 spełniają na przykład
spełniają na przykład 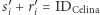 (zamiast
(zamiast 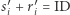 ), co sprawiłoby, że nie tylko będzie nieuchwytna, ale jeszcze wrobi Bogu ducha winną Celinę!
), co sprawiłoby, że nie tylko będzie nieuchwytna, ale jeszcze wrobi Bogu ducha winną Celinę!
Aby ostatecznie rozwiązać ten problem, potrzebne będzie odwołanie się do trzeciej części naszej sagi, w której pisaliśmy o dowodach z wiedzą zerową (zero-knowledge). Otóż poprawny protokół wygląda tak: Aldona i bank realizują protokół ślepego podpisu dla 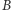 (wybranego przez Aldonę), ale bank, zanim ostatecznie (ślepo!) podpisze
(wybranego przez Aldonę), ale bank, zanim ostatecznie (ślepo!) podpisze 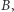 będzie oczekiwał dowodu (z wiedzą zerową!), że to, co podpisuje (choć tego nie widzi i nie zobaczy!), spełnia faktycznie warunek
będzie oczekiwał dowodu (z wiedzą zerową!), że to, co podpisuje (choć tego nie widzi i nie zobaczy!), spełnia faktycznie warunek 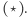 Szczegóły tego kroku są dość techniczne, wymagają oczywiście znajomości generycznego protokołu zero-knowledge dla języków klasy NP (prezentowanego w Delcie 01/2019), ale także podstawowej wiedzy o tym, czym w zasadzie są te języki i jak dowodzić przynależność do tej klasy. Pozwolę więc sobie tylko zakończyć ten finałowy fragment uwagą: to się naprawdę da zrobić, a dokładne uzupełnienie szczegółów może być bardzo trudną, ale i pouczającą intelektualną przygodą.
Szczegóły tego kroku są dość techniczne, wymagają oczywiście znajomości generycznego protokołu zero-knowledge dla języków klasy NP (prezentowanego w Delcie 01/2019), ale także podstawowej wiedzy o tym, czym w zasadzie są te języki i jak dowodzić przynależność do tej klasy. Pozwolę więc sobie tylko zakończyć ten finałowy fragment uwagą: to się naprawdę da zrobić, a dokładne uzupełnienie szczegółów może być bardzo trudną, ale i pouczającą intelektualną przygodą.
Postscriptum
Podkreślmy, że w tym artykule zajmowaliśmy się prawdziwie anonimową cyfrową gotówką. Należy sobie uzmysłowić, że ani Bitcoin (ani większość innych kryptowalut), ani tym bardziej standardowy system elektronicznej bankowości nie posiadają cechy anonimowości rozumianej tak, jak określiliśmy to na początku tego tekstu. Prawdziwie anonimowym systemem kryptowalutowym jest np. Zerocash, który również korzysta z dowodów z wiedzą zerową.
Postpostscriptum
Eksponowany w niniejszym tekście system autor artykułu zobaczył po raz pierwszy w świetnym eseju Ronalda Cramera, Ivana Damgarda oraz Jespera Buusa Nielsena pt. On Electronic Payment Systems. Użyty dokładnie tak, jak opisano go wyżej, nie jest niestety dostatecznie praktyczny (wąskim gardłem jest użycie generycznych dowodów z wiedzą zerową), ma za to duży walor edukacyjny. Protokołem opartym o tę samą ideę i korzystającym z podobnych technik - co prawda bardziej skomplikowanym (sic!), ale za to znacznie szybszym (praktycznym!) - jest natomiast protokół Brandsa. Czytelnik Bardzo Zaawansowany może sięgnąć do cytowanej powyżej pracy, w której znajdują się szczegóły również tego protokołu.
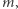 wybraną przez drugą stronę, a jednocześnie: nie mieć pojęcia, co podpisała.
wybraną przez drugą stronę, a jednocześnie: nie mieć pojęcia, co podpisała.