A jednak się da!
Protokół Yao (AJSD V)
Jedną z drobnych przyjemności w życiu milionera jest porównywanie swojego bogactwa z bogactwem innych milionerów. Czasem nie jest to trywialne zadanie, gdyż afiszowanie się ze stanem swojego konta (nawet przybliżonym) mogłoby zostać uznane za naruszenie krezusowej etykiety. Istnieje co prawda szeroki wachlarz subtelnych wskaźników, w rodzaju rozmiaru posiadłości czy liczby luksusowych aut, jednak te bywają bardzo mylące. Czy jest możliwa wymiana informacji między dwoma bogaczami w taki sposób, by każdy z nich dowiedział się, który z nich jest bogatszy, i byłaby to jedyna informacja o stanie posiadania rozmówcy?
Proponujemy Czytelnikowi zastanowienie się nad tym pytaniem przed sformułowaniem problemu ogólniejszego, czyli: czy jest to prawdą dla dowolnej wartości obliczanej na podstawie majątku obu rozmówców (na przykład: czy sumarycznie mają więcej niż miliard?). Oczywiście, tytuł naszej serii artykułów sugeruje twierdzącą odpowiedź na postawione pytanie i tak jest w rzeczywistości, a realizacją poszukiwanego sposobu jest protokół Yao.
Doprecyzujmy odrobinę nasze rozważania: każdy z dwojga rozmówców (podobnie, jak w poprzednich odcinkach sagi, niech będą to Aldona i Bogumił) skrywa pewną wartość. Dla ułatwienia dalszego opisu, przedstawmy te wartości w postaci binarnej i przechowujmy jako ciągi binarne o ustalonej z góry długości. Niech zatem wartością Aldony będzie 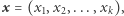 a wartością Bogumiła
a wartością Bogumiła 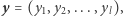 gdzie
gdzie 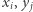 wynoszą 0 lub 1 dla
wynoszą 0 lub 1 dla 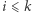 oraz
oraz 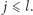 Aldona i Bogumił chcą obliczyć
Aldona i Bogumił chcą obliczyć 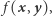 gdzie
gdzie 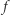 jest pewną znaną im funkcją, która przyjmuje wartości 0 lub 1 (taką funkcję będziemy nazywać boolowską). Jednocześnie każde z nich wymaga, by wszystko, czego dowiedziało się to drugie na podstawie wymienionych informacji, zawierało się w wartości funkcji
jest pewną znaną im funkcją, która przyjmuje wartości 0 lub 1 (taką funkcję będziemy nazywać boolowską). Jednocześnie każde z nich wymaga, by wszystko, czego dowiedziało się to drugie na podstawie wymienionych informacji, zawierało się w wartości funkcji 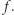 Gdyby na przykład funkcja
Gdyby na przykład funkcja 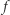 była iloczynem swoich argumentów i przyjęła wartość 0, a wśród argumentów Aldony były same 1, to jedyne, czego może się ona dowiedzieć o argumentach Bogumiła to tyle, że znajduje się wśród nich 0.
była iloczynem swoich argumentów i przyjęła wartość 0, a wśród argumentów Aldony były same 1, to jedyne, czego może się ona dowiedzieć o argumentach Bogumiła to tyle, że znajduje się wśród nich 0.
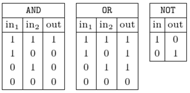
Konstrukcję protokołu Yao rozpoczniemy od przedstawienia funkcji 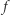 w postaci obwodu logicznego, czyli złożenia dwuargumentowych funkcji AND i OR oraz jednoargumentowej funkcji NOT. Oczywiste działanie tych funkcji przedstawione jest w tabelkach na marginesie. Czytelnikowi Dociekliwemu polecamy zastanowić się, jak każdą funkcję boolowską możemy zamienić na obwód logiczny - uzasadnienie jest ukryte tutaj. Kiedy już Aldona i Bogumił ustalą reprezentację rozważanej funkcji w postaci obwodu logicznego, przedstawiają go jako graf skierowany - przykład na rysunku 1 Możemy wyobrazić sobie, że jest to obwód elektryczny: krawędzie to przewody, którymi płynie (bądź nie) prąd, wierzchołki to "bramki", które wypuszczają (bądź nie) prąd w zależności od obecności prądu na ich "wejściach". (Przepływ prądu oczywiście reprezentuje bit 1, a brak przepływu - bit 0). Na dole są wierzchołki odpowiadające argumentom - są to "przełączniki", należące do Aldony lub Bogumiła, a na górze - wierzchołek odpowiadający wynikowi. Idea protokołu Yao (szczegóły zaraz) jest następująca: Aldona koduje w pewnym języku wszystkie możliwe zachowania obwodu i dostarcza Bogumiłowi tyle informacji, że potrafi on odtworzyć "prawdziwe" zachowanie obwodu w tym języku, bez ujawniania swoich argumentów i bez poznawania prawdziwych wartości argumentów Aldony. Precyzyjniej, procedura przebiega tak (realizacja niektórych punktów oznaczonych
w postaci obwodu logicznego, czyli złożenia dwuargumentowych funkcji AND i OR oraz jednoargumentowej funkcji NOT. Oczywiste działanie tych funkcji przedstawione jest w tabelkach na marginesie. Czytelnikowi Dociekliwemu polecamy zastanowić się, jak każdą funkcję boolowską możemy zamienić na obwód logiczny - uzasadnienie jest ukryte tutaj. Kiedy już Aldona i Bogumił ustalą reprezentację rozważanej funkcji w postaci obwodu logicznego, przedstawiają go jako graf skierowany - przykład na rysunku 1 Możemy wyobrazić sobie, że jest to obwód elektryczny: krawędzie to przewody, którymi płynie (bądź nie) prąd, wierzchołki to "bramki", które wypuszczają (bądź nie) prąd w zależności od obecności prądu na ich "wejściach". (Przepływ prądu oczywiście reprezentuje bit 1, a brak przepływu - bit 0). Na dole są wierzchołki odpowiadające argumentom - są to "przełączniki", należące do Aldony lub Bogumiła, a na górze - wierzchołek odpowiadający wynikowi. Idea protokołu Yao (szczegóły zaraz) jest następująca: Aldona koduje w pewnym języku wszystkie możliwe zachowania obwodu i dostarcza Bogumiłowi tyle informacji, że potrafi on odtworzyć "prawdziwe" zachowanie obwodu w tym języku, bez ujawniania swoich argumentów i bez poznawania prawdziwych wartości argumentów Aldony. Precyzyjniej, procedura przebiega tak (realizacja niektórych punktów oznaczonych 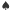 jest nietrywialna i będzie wytłumaczona w dalszej części tekstu):
jest nietrywialna i będzie wytłumaczona w dalszej części tekstu):
- (a)
- Aldona dla każdej krawędzi wybiera dwa kryptonimy: pierwszy koduje przepływ prądu przez daną krawędź, a drugi jego brak (Rys. 2). Bogumił do końca protokołu nie będzie w stanie połączyć żadnego kryptonimu z odpowiadającym mu bitem.
- (b)
 Aldona zamienia każdą bramkę na "czarną skrzynkę", która dla danych kryptonimów wejścia pozwala obliczyć adekwatny kryptonim wyjścia, i nic ponadto. Ten etap nazywany jest "garblowaniem" obwodu.
Aldona zamienia każdą bramkę na "czarną skrzynkę", która dla danych kryptonimów wejścia pozwala obliczyć adekwatny kryptonim wyjścia, i nic ponadto. Ten etap nazywany jest "garblowaniem" obwodu.- (c)
- Aldona przekazuje Bogumiłowi kryptonimy stanu swoich przełączników oraz wszystkie czarne skrzynki (wraz z informacją, jakim bramkom odpowiadają).
- (d)
 Bogumił poznaje hasła odpowiadające temu, czy z jego przełączników płynie prąd, w taki sposób, by Aldona niczego nie dowiedziała się o ich stanie.
Bogumił poznaje hasła odpowiadające temu, czy z jego przełączników płynie prąd, w taki sposób, by Aldona niczego nie dowiedziała się o ich stanie. - (e)
- Bogumił ewaluuje obwód w nowym języku (czyli po kolei, "od dołu", oblicza kryptonimy opisujące przepływ prądu przez kolejne przewody) i oblicza hasło wyniku (Rys. 3); przesyła je Aldonie.
- (f)
- Aldona tłumaczy kryptonim wyniku na prawdziwy wynik i przekazuje go Bogumiłowi.
Przeanalizujmy, w jaki sposób realizowane są założenia tego planu. Punkt a nie wymaga szczególnych objaśnień - w praktyce kryptonimami są duże liczby losowe, możemy jednak myśleć o bardziej swojskiej konwencji typu "pies/kot", "nos/oko" i tak dalej. Punkt b potrzebuje większej uwagi. W sukurs przychodzi nam szyfrowanie symetryczne. Przypomnijmy, że jest to podstawowy sposób szyfrowania, w którym do zakodowania i odkodowania wiadomości potrzebny jest ten sam klucz. Przykładem jest szyfr Cezara, w którym kluczem jest liczba pozycji, o jaką przesuwamy w alfabecie każdą literę wiadomości. Warto zwrócić uwagę na pewną własność szyfru Cezara - jeśli spróbujemy odczytać zakodowaną wiadomość (czyli szyfrogram) przy użyciu błędnego klucza, otrzymamy zapewne bezsensowny ciąg liter, przez co dowiemy się, że użyty przez nas klucz był nieprawidłowy. Podobną własność można wymusić na każdym szyfrze symetrycznym - wystarczy umówić się, że przekazywane przez nas wiadomości muszą mieć pewną szczególną własność (na przykład być słowami w pewnym języku, jak w przypadku szyfru Cezara, lub zaczynać się ustalonej długości ciągiem jedynek). Wówczas użycie błędnego klucza z dużym prawdopodobieństwem "wyrzuci" nas poza dopuszczalny zbiór wiadomości, przez co dowiemy się, że coś poszło nie tak. Od naszego szyfru wymagać ponadto będziemy, by znajomość wiadomości i szyfrogramu nie pozwalała na obliczenie klucza. Dyskwalifikuje to niestety szyfr Cezara, jednak na szczęście stosowane szyfry symetryczne najczęściej mają tę własność.
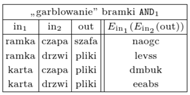
Tłumaczenie działania bramki 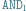 na język kryptonimów, a następnie kodowanie każdego kryptonimu wyjścia przy użyciu odpowiednich kryptonimów wejścia i pewnej funkcji szyfrującej
na język kryptonimów, a następnie kodowanie każdego kryptonimu wyjścia przy użyciu odpowiednich kryptonimów wejścia i pewnej funkcji szyfrującej 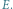
Jak w takim razie może wyglądać "czarna skrzynka", której potrzebuje Aldona? Wystarczy dla każdej z czterech (lub dwóch, dla bramki NOT) możliwych kombinacji kryptonimów wejścia obliczyć kryptonim odpowiadającego im wyjścia, po czym zaszyfrować je dwukrotnie przy użyciu najpierw kryptonimu wejścia 1, a następnie kryptonimu wejścia 2, a na koniec ustawić wyniki w losowej kolejności. Brzmi skomplikowanie, jednak analiza przykładu przedstawionego na marginesie powinna rozjaśnić wszelkie wątpliwości. Zauważmy, że mając tak uzyskane cztery szyfrogramy oraz dwa konkretne kryptonimy wejścia, Bogumił może obliczyć kryptonim wyjścia - wystarczy, że odkoduje wszystkie szyfrogramy przy użyciu posiadanych kryptonimów wejścia. Dostanie wówczas trzykrotnie "śmieci" oraz jednokrotnie pełnoprawny kryptonim, który jest szukanym kryptonimem wyjścia. Podkreślmy, że w ten sposób nie dowiaduje się on niczego o znaczeniu kryptonimów wejścia! Jeśli zatem Bogumił dostanie wszystkie czarne skrzynki oraz kryptonimy stanu swoich i Aldony przełączników (punkty c i d), będzie mógł obliczyć kryptonimy wyników kolejnych bramek, nie poznając bezpośrednio rzeczywistego stanu przełączników Aldony (punkt e). Czy może on jednak poznać kryptonimy stanu swoich przełączników tak, by nie ujawnić Aldonie ich rzeczywistej pozycji (punkt d)? Jak najbardziej (choć jest to nietrywialne) - pisaliśmy o tym w poprzednim odcinku naszej serii Delta 2/2019), a stosowny protokół to transfer utajniony. Wszystkie brakujące elementy układanki są już zatem na swoim miejscu, a Aldona i Bogumił mogą śmiało obliczać wartości funkcji bez obaw o ujawnienie swoich sekretów.
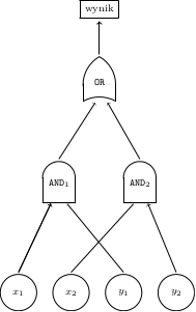
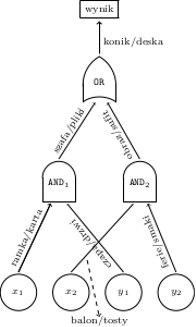
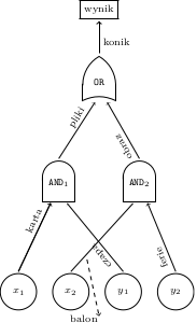
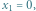
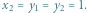 Dla żadnej krawędzi nie poznaje on kryptonimu odpowiadającego jej "drugiemu" stanowi.
Dla żadnej krawędzi nie poznaje on kryptonimu odpowiadającego jej "drugiemu" stanowi.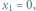
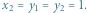 Dla żadnej krawędzi nie poznaje on kryptonimu odpowiadającego jej "drugiemu" stanowi.
Dla żadnej krawędzi nie poznaje on kryptonimu odpowiadającego jej "drugiemu" stanowi.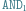 to
to 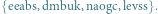 Jeśli Bogumił poznał tę czarną skrzynkę oraz wie, że kryptonimy wejścia do tej bramki to "karta" i "czapa", to odkodowuje każdy element czarnej skrzynki przy użyciu tych kryptonimów i stąd otrzymuje kryptonim wyniku. Dla przykładu, jeśli otrzymał w ten sposób
Jeśli Bogumił poznał tę czarną skrzynkę oraz wie, że kryptonimy wejścia do tej bramki to "karta" i "czapa", to odkodowuje każdy element czarnej skrzynki przy użyciu tych kryptonimów i stąd otrzymuje kryptonim wyniku. Dla przykładu, jeśli otrzymał w ten sposób 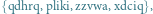 to dowiaduje się, że kryptonim wyniku to "pliki".
to dowiaduje się, że kryptonim wyniku to "pliki".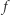 przyjmuje wartość 1 tylko dla na przykład
przyjmuje wartość 1 tylko dla na przykład 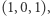 to szukany obwód logiczny ma postać
to szukany obwód logiczny ma postać 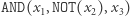 (co prawda
(co prawda 