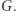A jednak się da!
O dowodach z wiedzą zerową (AJSD III)
Bywa tak, że chcemy o czymś przekonać niedowiarków, jednak w taki sposób, aby uwierzyli, ale też aby za dużo się nie dowiedzieli. Fabularna, nieinformatyczna ilustracja, którą lubię przywoływać, gdy próbuję wyrazić, o co mi chodzi, jest następująca. Wyobraźmy sobie, że potrafię zliczyć liczbę liści na drzewie, jeśli tylko spojrzę na nie przez 5 sekund. Więcej: twierdzę, że umiem to publicznie udowodnić w przeciągu 5 minut, i to tak, że wszyscy mi uwierzą, ale nikt się nie zorientuje, jak ja to robię!
Jak mógłby wyglądać protokół, który realizuje powyższe założenia? Popatrzmy:
- (1)
- Proszę publiczność o wskazanie dowolnego drzewa.
- (2)
- Patrzę na to drzewo przez 5 sekund i mówię: "to drzewo ma
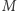 liści".
liści". - (3)
- Proszę publiczność o zawiązanie mi oczu.
- (4)
- Proszę publiczność o podejście do analizowanego drzewa i zerwanie z niego dowolnych
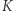 liści (oczywiście
liści (oczywiście 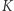 publiczność ustala samodzielnie, nie informując mnie o swoim wyborze).
publiczność ustala samodzielnie, nie informując mnie o swoim wyborze). - (5)
- Proszę publiczność o rozwiązanie mi oczu.
- (6)
- Ponownie patrzę na drzewo przez 5 sekund i mówię: "to drzewo ma
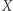 liści".
liści".

I teraz tak: jeśli 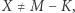 to z pewnością nikogo nie przekonałem. Jednak jeśli
to z pewnością nikogo nie przekonałem. Jednak jeśli 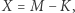 to eksperyment daje do myślenia. Oczywiście, aby zmniejszyć szansę zdarzenia, że po prostu miałem szczęście, protokół weryfikacyjny można kilka razy powtórzyć, dla różnych drzew i różnych wyborów zmiennej
to eksperyment daje do myślenia. Oczywiście, aby zmniejszyć szansę zdarzenia, że po prostu miałem szczęście, protokół weryfikacyjny można kilka razy powtórzyć, dla różnych drzew i różnych wyborów zmiennej 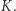 Jeśli więc pozytywnie przejdę na przykład 10 testów pod rząd, to sądzę, że już wszyscy mi uwierzą, że naprawdę umiem błyskawicznie zliczać liście na drzewie. Mimo to: nikt nie ma nawet cienia wskazówki, jak ja to robię!
Jeśli więc pozytywnie przejdę na przykład 10 testów pod rząd, to sądzę, że już wszyscy mi uwierzą, że naprawdę umiem błyskawicznie zliczać liście na drzewie. Mimo to: nikt nie ma nawet cienia wskazówki, jak ja to robię!
Właśnie takie przekonywanie jak wyżej nazywamy fachowo dowodzeniem z wiedzą zerową (zero-knowledge proofs), a bardziej kolokwialnie: przekomarzaniem się w stylu "wiem, ale nie powiem". Okazuje się, że zaskakująco wiele stwierdzeń matematycznych da się udowodnić w taki właśnie sposób. W szczególności: gdybyśmy na przykład potrafili rozstrzygnąć pozytywnie hipotezę Riemanna, to możemy zaproponować światu pewną zabawę, w wyniku której wszyscy uwierzą, że faktycznie hipoteza Riemanna jest prawdziwa, ale nikt nawet powierzchownie nie liźnie smaku naszego dowodu. Jak to zrobić - obiecuję naszkicować na końcu, a na razie zajmijmy się prostszym przykładem.
Izomorfizm grafów
Opiszemy protokół dowodu z wiedzą zerową dla problemu izomorfizmu grafów (szerzej o tym problemie pisał Łukasz Kowalik w Delcie 12/2018). Przypomnijmy: problem polega na rozstrzygnięciu, czy dwa dane grafy 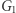 oraz
oraz 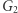 są izomorficzne, czy też nie. Załóżmy więc, że znamy pewien izomorfizm
są izomorficzne, czy też nie. Załóżmy więc, że znamy pewien izomorfizm  między
między 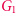 a
a 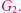 Naszym celem jest przekonać publiczność (fachowo: weryfikatora), że faktycznie znamy
Naszym celem jest przekonać publiczność (fachowo: weryfikatora), że faktycznie znamy 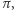 ale bez ujawniania, jak to
ale bez ujawniania, jak to 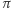 w rzeczywistości wygląda.
w rzeczywistości wygląda.
Do dzieła:
- (1)
- Postulujemy publicznie, że grafy
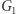 oraz
oraz 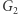 są izomorficzne.
są izomorficzne. - (2)
- Publikujemy dowolny graf
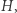 który jest izomorficzny z
który jest izomorficzny z 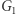 (czyli również z
(czyli również z 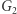 ).
). - (3)
- Weryfikator wybiera liczbę
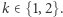
- (4)
- Publikujemy izomorfizm
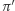 między
między 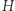 a
a 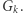
- (5)
- Weryfikator sprawdza, czy
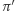 jest rzeczywiście poprawnym izomorfizmem między
jest rzeczywiście poprawnym izomorfizmem między 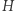 a
a 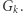
- (6)
- Kroki 2-5 powtarzamy
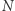 razy.
razy.
Powyższy protokół ma trzy kluczowe cechy:
- (a)
- Jeśli naprawdę znamy postulowany izomorfizm, to jesteśmy zawsze w stanie wykonać poprawnie cały protokół;
- (b)
- Szansa, że oszukamy weryfikatora (to znaczy: przekonamy go, że znamy izomorfizm między
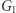 a
a 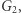 mimo że wcale go nie znamy) wynosi co najwyżej
mimo że wcale go nie znamy) wynosi co najwyżej 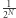 ;
; - (c)
- Przekonany weryfikator nie ma bladego pojęcia, jak może wyglądać izomorfizm między
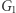 a
a 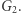
Naszkicujmy więc uzasadnienia stwierdzeń b oraz c (pozwolimy sobie napisać, że a jest trywialne):
Ad (b) Zauważmy, że jeśli odnosimy sukces z prawdopodobieństwem powyżej 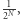 to przynajmniej w jednej z
to przynajmniej w jednej z 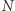 iteracji protokołu, w kroku 4. byliśmy przygotowani na opublikowanie izomorfizmu zarówno między
iteracji protokołu, w kroku 4. byliśmy przygotowani na opublikowanie izomorfizmu zarówno między 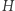 a
a 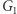 (ozn.
(ozn. 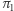 ), jak i między
), jak i między 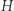 a
a 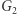 (ozn.
(ozn. 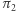 ). Istotnie - gdyby tak nie było, to w każdej iteracji mielibyśmy szansę co najwyżej
). Istotnie - gdyby tak nie było, to w każdej iteracji mielibyśmy szansę co najwyżej 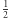 na akceptację przez weryfikatora, a więc ogólnie - co najwyżej tylko
na akceptację przez weryfikatora, a więc ogólnie - co najwyżej tylko 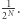 Jednak znajomość zarówno
Jednak znajomość zarówno 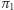 jak i
jak i 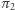 oznacza również znajomość
oznacza również znajomość 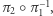 a to jest przecież izomorfizm między
a to jest przecież izomorfizm między 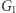 a
a 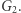
Ad (c) Zastanówmy się, czego - po wykonaniu całego protokołu - dowiedział się weryfikator. Jak widać, poznał 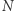 różnych trójek postaci
różnych trójek postaci 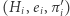 takich, że
takich, że 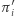 jest izomorfizmem między
jest izomorfizmem między 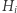 a
a 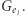 Czy taka wiedza jest w jakikolwiek sposób ekskluzywna? Otóż łatwo zauważyć, że absolutnie nie - przecież takie trójki można sobie samemu (w dowolnych ilościach) produkować, znając wyłącznie
Czy taka wiedza jest w jakikolwiek sposób ekskluzywna? Otóż łatwo zauważyć, że absolutnie nie - przecież takie trójki można sobie samemu (w dowolnych ilościach) produkować, znając wyłącznie 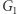 oraz
oraz 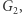 a te są przecież publiczne od samego początku!
a te są przecież publiczne od samego początku!
Cykl Hamiltona w grafie
Czas na nieco bardziej skomplikowany przykład - protokół dowodu z wiedzą zerową dla problemu istnienia cyklu Hamiltona w grafie.
W tym protokole będziemy używać idei zobowiązań  opisanych przez Łukasza Rajkowskiego w poprzednim odcinku AJSD, w Delcie 11/2018.
opisanych przez Łukasza Rajkowskiego w poprzednim odcinku AJSD, w Delcie 11/2018.
Jak poprzednio, załóżmy, że znamy cykl Hamiltona 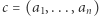 pewnego grafu
pewnego grafu 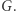 Teraz:
Teraz:
- (1)
- Postulujemy publicznie, że w
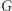 istnieje cykl Hamiltona. Będziemy próbować to udowodnić, ale nie zdradzając, jak faktycznie wygląda
istnieje cykl Hamiltona. Będziemy próbować to udowodnić, ale nie zdradzając, jak faktycznie wygląda 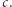
- (2)
- Losujemy dowolną permutację
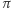 oraz obliczamy graf
oraz obliczamy graf 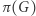 (czyli izomorficzny do
(czyli izomorficzny do 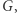 ale z wierzchołkami spermutowanymi według
ale z wierzchołkami spermutowanymi według 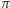 ).
). - (3)
- Upubliczniamy następujące zobowiązania:
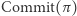
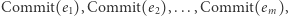 gdzie
gdzie 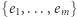 stanowią opisy wszystkich krawędzi grafu
stanowią opisy wszystkich krawędzi grafu 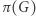 (to znaczy: każde
(to znaczy: każde 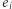 jest parą pewnych wierzchołków grafu
jest parą pewnych wierzchołków grafu 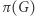 ).
).
- (4)
- Weryfikator wybiera liczbę
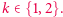
- (5)
- Jeśli
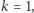 to otwieramy wszystkie (zarówno permutacji, jak i krawędzi) zobowiązania z kroku 3.
to otwieramy wszystkie (zarówno permutacji, jak i krawędzi) zobowiązania z kroku 3. - (6)
- Jeśli
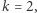 to otwieramy zobowiązania tych (i tylko tych) krawędzi, które tworzą cykl Hamiltona w
to otwieramy zobowiązania tych (i tylko tych) krawędzi, które tworzą cykl Hamiltona w 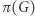 (NIE otwieramy zobowiązania permutacji!).
(NIE otwieramy zobowiązania permutacji!). - (7)
- Jeśli
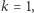 to weryfikator sprawdza, czy otwarte krawędzie
to weryfikator sprawdza, czy otwarte krawędzie 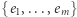 są faktycznie krawędziami grafu
są faktycznie krawędziami grafu 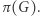
- (8)
- Jeśli
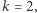 to weryfikator sprawdza, czy faktycznie otwarte krawędzie tworzą jeden zamknięty cykl długości
to weryfikator sprawdza, czy faktycznie otwarte krawędzie tworzą jeden zamknięty cykl długości 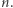
- (9)
- Kroki 2-8 powtarzamy
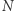 razy.
razy.
Twierdzimy, że ten protokół również ma trzy cechy, o których mówiliśmy w poprzednim przykładzie. To znaczy: jeśli rzeczywiście znamy cykl Hamiltona w 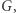 to wykonamy protokół bez problemu (trywialna obserwacja). Dalej: szansa na oszukanie weryfikatora wynosi ponownie co najwyżej
to wykonamy protokół bez problemu (trywialna obserwacja). Dalej: szansa na oszukanie weryfikatora wynosi ponownie co najwyżej 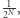 a schemat dowodu jest dokładnie taki sam jak poprzednio. Wystarczy tylko zauważyć, że jeśli w którejkolwiek iteracji jesteśmy pewni akceptacji weryfikatora (niezależnie od wyboru
a schemat dowodu jest dokładnie taki sam jak poprzednio. Wystarczy tylko zauważyć, że jeśli w którejkolwiek iteracji jesteśmy pewni akceptacji weryfikatora (niezależnie od wyboru 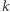 ), to znaczy, że zobowiązaliśmy się do permutacji
), to znaczy, że zobowiązaliśmy się do permutacji 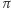 takiej, że znamy cykl Hamiltona w
takiej, że znamy cykl Hamiltona w 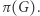 To jednak oznacza, że znamy również cykl Hamiltona w
To jednak oznacza, że znamy również cykl Hamiltona w 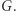 Pozostaje tylko upewnić się, że nabyta (w wyniku realizacji protokołu) przez weryfikatora wiedza nic mądrego mu nie mówi. I tak jest w istocie: jeśli
Pozostaje tylko upewnić się, że nabyta (w wyniku realizacji protokołu) przez weryfikatora wiedza nic mądrego mu nie mówi. I tak jest w istocie: jeśli 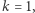 to weryfikator uczy się tylko pewnego izomorfizmu
to weryfikator uczy się tylko pewnego izomorfizmu 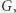 a jeśli
a jeśli 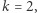 to weryfikator poznaje losową permutację liczb
to weryfikator poznaje losową permutację liczb 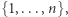 zupełnie niezależną od
zupełnie niezależną od 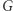 (bo w tym przypadku nie zna
(bo w tym przypadku nie zna 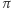 !).
!).
Co jeszcze?
Pokazaliśmy dwa przykłady protokołów dowodów z wiedzą zerową. Nasuwa się pytanie: jakie inne (i jak bardzo skomplikowane) stwierdzenia możemy podobnie dowodzić? Okazuje się (być może zaskakująco), że... niemal wszystkie. Aby się o tym przekonać, potrzebna jest pewna wiedza z teorii złożoności obliczeniowej, a konkretnie: informacja, że problem istnienia cyklu Hamiltona w grafie jest problemem NP-zupełnym. Nie jest ambicją tego artykułu, aby dokładnie wytłumaczyć to pojęcie (patrz na przykład Delta 11/2013, Delta 1/2017 czy Delta 11/2017), więc siłą rzeczy musimy w tym momencie trochę rozluźnić rygor ścisłej precyzji na rzecz intuicji.
Otóż fakt, że problem cyklu Hamiltona (CH) jest NP-zupełny, oznacza, że dzięki temu, że pokazaliśmy protokół dowodu z wiedzą zerową dla CH, wiemy jak konstruować protokoły z wiedzą zerową dla dowolnego innego problemu z klasy NP! W jaki sposób? Wystarczy zastosować odpowiednią efektywną redukcję do problemu CH (która musi zawsze istnieć) i dalej stosować protokół opisany wyżej.
W szczególności: załóżmy, że udowodniliśmy hipotezę Riemanna. Rozważmy teraz język:

Niewątpliwie 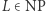 (dlaczego?), więc dla każdego
(dlaczego?), więc dla każdego 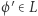 istnieje dowód z wiedzą zerową, w szczególności: dla
istnieje dowód z wiedzą zerową, w szczególności: dla 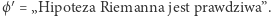
A po ludzku: okazuje się, że istnieje graf 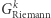 (rozmiaru wielomianowego od
(rozmiaru wielomianowego od 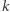 ) taki, że jeśli hipoteza Riemanna ma dowód długości
) taki, że jeśli hipoteza Riemanna ma dowód długości 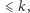 to w tym grafie jest cykl Hamiltona, a jeśli nie ma takiego dowodu - to i cyklu Hamiltona w
to w tym grafie jest cykl Hamiltona, a jeśli nie ma takiego dowodu - to i cyklu Hamiltona w 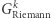 nie znajdziemy. Więcej: znalezienie grafu
nie znajdziemy. Więcej: znalezienie grafu 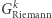 jest efektywnie obliczalną funkcją zdania
jest efektywnie obliczalną funkcją zdania 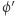 (zapisanego w jakiejś formalnej logice). Jeśli więc rzeczywiście znajdziemy dowód dla hipotezy Riemanna długości
(zapisanego w jakiejś formalnej logice). Jeśli więc rzeczywiście znajdziemy dowód dla hipotezy Riemanna długości 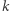 i mamy nieodpartą pokusę pohandryczyć się ze światem, to możemy zawsze przedstawić wyłącznie dowód istnienia cyklu Hamiltona w grafie
i mamy nieodpartą pokusę pohandryczyć się ze światem, to możemy zawsze przedstawić wyłącznie dowód istnienia cyklu Hamiltona w grafie 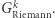 Dowód z wiedzą zerową, rzecz jasna!
Dowód z wiedzą zerową, rzecz jasna!
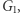 jak i
jak i 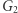 to
to 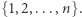 Permutacja
Permutacja 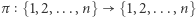 jest izomorfizmem między
jest izomorfizmem między 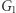 a
a 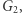 gdy dla każdej pary
gdy dla każdej pary 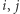 spełniony jest warunek: w
spełniony jest warunek: w 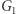 istnieje krawędź między wierzchołkami
istnieje krawędź między wierzchołkami 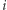 a
a 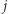 wtedy i tylko wtedy, gdy w
wtedy i tylko wtedy, gdy w 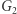 istnieje krawędź między wierzchołkami
istnieje krawędź między wierzchołkami 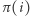 a
a 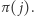
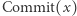 praktycznie nie jest możliwe odczytanie
praktycznie nie jest możliwe odczytanie  Otworzyć zobowiązanie (ujawniając
Otworzyć zobowiązanie (ujawniając  ) może tylko jego autor, przy czym - nie jest w stanie oszukać, czyli wmówić, że w zobowiązaniu znajdował się jakiś
) może tylko jego autor, przy czym - nie jest w stanie oszukać, czyli wmówić, że w zobowiązaniu znajdował się jakiś 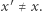
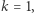 to weryfikator sprawdza, czy nie oszukujemy przy konstruowaniu
to weryfikator sprawdza, czy nie oszukujemy przy konstruowaniu 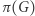 ; jeśli
; jeśli 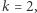 to weryfikator sprawdza, czy w zobowiązanym grafie faktycznie jest cykl Hamiltona; żadna z tych informacji pojedynczo nie pozwala na odtworzenie cyklu Hamiltona w
to weryfikator sprawdza, czy w zobowiązanym grafie faktycznie jest cykl Hamiltona; żadna z tych informacji pojedynczo nie pozwala na odtworzenie cyklu Hamiltona w 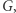 jednak aby przygotować zobowiązania z kroku 3 tak, aby mieć pewność przejścia obu testów w krokach 7-8, TRZEBA znać cykl Hamiltona w
jednak aby przygotować zobowiązania z kroku 3 tak, aby mieć pewność przejścia obu testów w krokach 7-8, TRZEBA znać cykl Hamiltona w