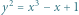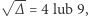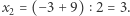Krzywe eliptyczne w kryptografii
Tak zwana "kryptografia krzywych eliptycznych" to bardzo modne i popularne pojęcie, które rzeczywiście jest ważne, ale - niestety - o którym mówi się najczęściej niezwykle powierzchownie, bez wchodzenia w "detale matematyczne". Niniejszy artykuł próbuje pójść takiemu podejściu pod prąd - chcemy w elementarny sposób objaśnić, o co tak naprawdę chodzi z tymi krzywymi eliptycznymi.
1. Bestiariusz algebraika
Wybierzmy i ustalmy sobie jakąś liczbę pierwszą 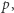 na przykład
na przykład 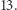 Na początku będziemy zajmować się zbiorem:
Na początku będziemy zajmować się zbiorem:

W tym zbiorze wykonywać będziemy działania dodawania i mnożenia, ale nie klasycznie, lecz zgodnie z arytmetyką modulo, czyli po prostu reszt z dzielenia. To znaczy, w naszym świecie będziemy mieli:

Co ciekawe, w tak dziwacznej strukturze zaskakująco wiele własności zwykłych liczb rzeczywistych jest zachowanych. Znane jeszcze ze szkoły podstawowej prawa łączności, przemienności czy rozdzielności mnożenia względem dodawania są prawdziwe także w 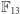 z działaniami modulo. Możemy nawet sensownie określić odejmowanie i dzielenie jako operacje odwrotne do (odpowiednio) dodawania i mnożenia. Przykładowo określmy:
z działaniami modulo. Możemy nawet sensownie określić odejmowanie i dzielenie jako operacje odwrotne do (odpowiednio) dodawania i mnożenia. Przykładowo określmy:

Możemy łatwo sprawdzić, że - przy powyższej definicji - zachodzi  czy
czy 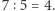 Więcej, okazuje się, że jeśli tylko nie próbujemy dzielić przez
Więcej, okazuje się, że jeśli tylko nie próbujemy dzielić przez 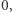 to wynik zawsze istnieje i to jednoznaczny.
to wynik zawsze istnieje i to jednoznaczny.
Pójdźmy krok dalej i zacznijmy badać równania w świecie  Zapytajmy chociażby o rozwiązania następującego równania kwadratowego:
Zapytajmy chociażby o rozwiązania następującego równania kwadratowego:

Możemy sprawdzić, że rozwiązania są dokładnie dwa: 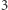 oraz
oraz  Ba, działają nawet klasyczne wzory z deltą, o ile tylko określimy sensownie pierwiastkowanie modulo.
Ba, działają nawet klasyczne wzory z deltą, o ile tylko określimy sensownie pierwiastkowanie modulo.
Oczywiście, ma sens pytanie o zbiory, których definicja kojarzy nam się z obiektami klasycznej geometrii. Chociażby popatrzmy na zbiór:

Możemy po prostu obliczyć, że

a otrzymany zbiór  nazwać okręgiem nad
nazwać okręgiem nad  choć to przecież żaden prawdziwy okrąg, a tylko 12 punktów iloczynu kartezjańskiego
choć to przecież żaden prawdziwy okrąg, a tylko 12 punktów iloczynu kartezjańskiego 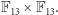 Niemniej tego typu obiekty są bardzo użyteczne i intensywnie badane przez dziedzinę matematyki zwaną geometrią algebraiczną. W tym artykule chcemy przybliżyć przykład takiego obiektu - tak zwane krzywe eliptyczne, czyli punkty spełniające równanie:
Niemniej tego typu obiekty są bardzo użyteczne i intensywnie badane przez dziedzinę matematyki zwaną geometrią algebraiczną. W tym artykule chcemy przybliżyć przykład takiego obiektu - tak zwane krzywe eliptyczne, czyli punkty spełniające równanie:

dla pewnych ustalonych 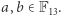

Rys. 1 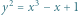

Rys. 2 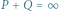
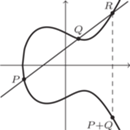
Rys. 3
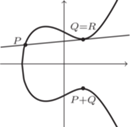
Rys. 4
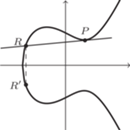
Rys. 5
Zanim powrócimy do właśnie przedstawionych krzywych eliptycznych nad ciałem 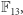 przyjrzyjmy się jeszcze ich rzeczywistym odpowiednikom, tzn. krzywym typu
przyjrzyjmy się jeszcze ich rzeczywistym odpowiednikom, tzn. krzywym typu

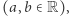 których przykład możemy obejrzeć na rysunku 1. Udziwnijmy świat punktów tej krzywej. Dorzućmy do
których przykład możemy obejrzeć na rysunku 1. Udziwnijmy świat punktów tej krzywej. Dorzućmy do  jeden nowy punkt specjalny:
jeden nowy punkt specjalny:  (nieskończoność), a w powstałym zbiorze
(nieskończoność), a w powstałym zbiorze 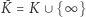 zdefiniujmy następujące dodawanie punktów (tzn. pewną operację
zdefiniujmy następujące dodawanie punktów (tzn. pewną operację 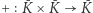 ):
):
- dla dowolnego
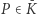 mamy
mamy  ;
; - Jeśli dwa różne punkty
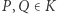 mają tę samą pierwszą współrzędną (jak na rysunku 2), to
mają tę samą pierwszą współrzędną (jak na rysunku 2), to 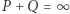 ;
; - Jeśli dwa różne punkty
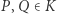 mają różną pierwszą współrzędną, to rysujemy prostą przechodzącą przez
mają różną pierwszą współrzędną, to rysujemy prostą przechodzącą przez 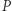 i
i 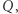 zaznaczamy trzeci punkt przecięcia z krzywą
zaznaczamy trzeci punkt przecięcia z krzywą 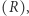 a ostatecznym wynikiem dodawania
a ostatecznym wynikiem dodawania 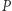 i
i 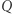 jest odbicie symetryczne
jest odbicie symetryczne 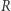 względem osi
względem osi 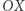 (Rys. 3). Może się zdarzyć, że dorysowana prosta nie przetnie się w żadnym dodatkowym punkcie (jak na rysunku 4). Wówczas dorysowana prosta na pewno będzie styczna do naszej krzywej i jako punkt
(Rys. 3). Może się zdarzyć, że dorysowana prosta nie przetnie się w żadnym dodatkowym punkcie (jak na rysunku 4). Wówczas dorysowana prosta na pewno będzie styczna do naszej krzywej i jako punkt 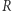 należy przyjąć punkt styczności.
należy przyjąć punkt styczności. - Jeśli liczymy
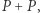 to rysujemy styczną do
to rysujemy styczną do 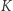 w punkcie
w punkcie 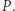 Jeśli ta styczna nie przecina się z
Jeśli ta styczna nie przecina się z 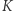 w żadnym innym punkcie, to
w żadnym innym punkcie, to 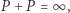 w przeciwnym razie (prosta przecina się jeszcze w punkcie
w przeciwnym razie (prosta przecina się jeszcze w punkcie 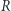 )
) 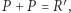 gdzie
gdzie 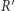 jest odbiciem symetrycznym
jest odbiciem symetrycznym 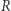 względem osi
względem osi 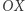 (zob. Rys. 5).
(zob. Rys. 5).
Jak widać, dodawanie punktów jest zdefiniowane w pełni geometrycznie. Jednakże możemy to samo działanie (sprawdź! - jest to żmudne, ale proste) opisać analitycznie. Gdy 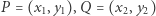 i
i 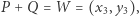 dla
dla  mamy
mamy

a gdy 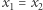 oraz
oraz 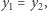 wzory są następujące:
wzory są następujące:

Forma analityczna dodawania punktów jest wygodniejsza, ponieważ pozwala na zdefiniowanie dodawania punktów również w zbiorze 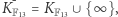 poprzez zwykłą analogię. To znaczy umawiamy się, że powyższe wzory analityczne (mające sens również w arytmetyce modulo 13) na
poprzez zwykłą analogię. To znaczy umawiamy się, że powyższe wzory analityczne (mające sens również w arytmetyce modulo 13) na 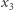 i
i 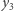 określają dodawanie punktów również w
określają dodawanie punktów również w 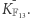
Dodawanie punktów na krzywej (zarówno w  jak i w
jak i w 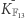 ) jest działaniem o ładnych własnościach: jest łączne, ma element neutralny (tutaj
) jest działaniem o ładnych własnościach: jest łączne, ma element neutralny (tutaj  ) oraz własność, że każdy element
) oraz własność, że każdy element 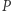 ma element odwrotny
ma element odwrotny 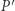 (czyli taki, że
(czyli taki, że 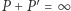 ). Struktury o takich własnościach zwyczajowo nazywamy grupą. Przykładem grupy innej niż te dwie opisane wyżej może być też
). Struktury o takich własnościach zwyczajowo nazywamy grupą. Przykładem grupy innej niż te dwie opisane wyżej może być też 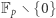 z działaniem mnożenia modulo
z działaniem mnożenia modulo 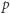 (warto samemu sprawdzić). Dla nas te grupy będą mieć jednak jeszcze jedną bardzo ważną własność, związaną z trudnością obliczeniową. O tym już za chwilkę.
(warto samemu sprawdzić). Dla nas te grupy będą mieć jednak jeszcze jedną bardzo ważną własność, związaną z trudnością obliczeniową. O tym już za chwilkę.
2. Bestia na usługach kryptografii
Wiele protokołów szyfrowania w kryptografii opiera się na trudności obliczeniowej różnych problemów. Pewnie najsłynniejsze jest szyfrowanie RSA, którego bezpieczeństwo gwarantowane jest przez trudność faktoryzacji dużych liczb. Są jednak i inne protokoły (np. szyfr El-Gamal), których bezpieczeństwo opiera się na innym założeniu, mianowicie na trudności obliczania logarytmu dyskretnego. Na czym to polega? Chodzi o problem znalezienia w danej grupie 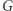 z mnożeniem dla danych
z mnożeniem dla danych  takiego
takiego 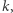 że
że

bądź w wersji z grupą z dodawaniem takiego 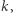 że:
że:

Oczywiście, nie dla każdej grupy problem logarytmu dyskretnego jest trudny. Dla grupy  z dodawaniem jest on banalny (dlaczego?), ale dla tego samego
z dodawaniem jest on banalny (dlaczego?), ale dla tego samego  tylko z mnożeniem - już uchodzi za trudny. Konkretnie, najszybszy znany algorytm dla tego problemu działa w czasie
tylko z mnożeniem - już uchodzi za trudny. Konkretnie, najszybszy znany algorytm dla tego problemu działa w czasie

co dla 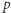 rozsądnie dużych rozmiarów jest już poza zasięgiem współczesnych komputerów.
rozsądnie dużych rozmiarów jest już poza zasięgiem współczesnych komputerów.
Po co więc te całe krzywe eliptyczne? Po prostu najszybsze algorytmy rozwiązujące logarytm dyskretny dla losowej krzywej postaci 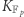 są jeszcze wolniejsze niż algorytmy dla grupy
są jeszcze wolniejsze niż algorytmy dla grupy 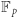 podobnego rozmiaru. Konkretnie dla krzywych eliptycznych wszystkie znane ogólne algorytmy rozwiązujące problem logarytmu dyskretnego działają w czasie
podobnego rozmiaru. Konkretnie dla krzywych eliptycznych wszystkie znane ogólne algorytmy rozwiązujące problem logarytmu dyskretnego działają w czasie

Oznacza to, że każdy protokół kryptograficzny, oparty o problem logarytmu dyskretnego, staje się bezpieczniejszy bez zwiększenia 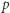 (a więc bez zwiększenia rozmiaru kluczy), jeśli tylko zmienimy grupę, z którą pracujemy, z
(a więc bez zwiększenia rozmiaru kluczy), jeśli tylko zmienimy grupę, z którą pracujemy, z 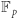 z mnożeniem na
z mnożeniem na 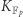 z dodawaniem punktów. Dokładnie z tego powodu już nie jest popularne używanie podpisu cyfrowego DSA (z roku 1991), a powszechnie używa się podpisu ECDSA (z roku 1999) - czyli jego odpowiednika, ale opartego o krzywe eliptyczne.
z dodawaniem punktów. Dokładnie z tego powodu już nie jest popularne używanie podpisu cyfrowego DSA (z roku 1991), a powszechnie używa się podpisu ECDSA (z roku 1999) - czyli jego odpowiednika, ale opartego o krzywe eliptyczne.
A jednak ta geometria algebraiczna gdzieś się przydaje!